Transformerに分岐処理を行うMoE(Mixture of Experts)を導入することで計算コストを大きく増やさずにパラメータ数を増やすことが可能になります。当記事ではこのような方針に基づいてTransformerの学習を行った研究であるSwitch Transformerについて取りまとめを行いました。
MoE(Mixture of Experts)論文や、Switch Transformers論文などの内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
Transformer
Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。
・直感的に理解するTransformerの仕組み(統計の森作成)
MoEとSwich Transformersの仕組み
Switch Transformersの概要
Switch Transformersでは大まかに下図のような処理が行われます。
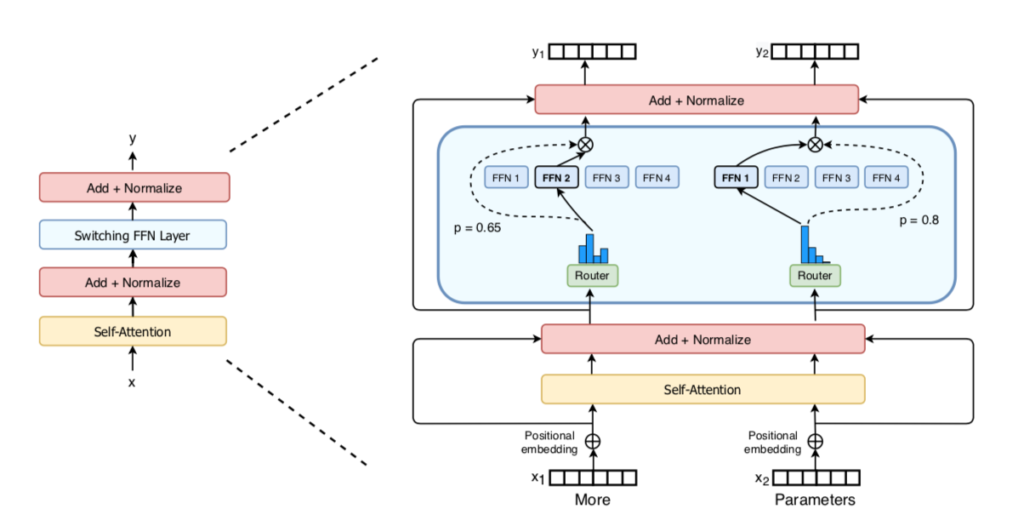
図の左が通常のTransformerにおける処理を表しており、オレンジのブロックがself-attention、水色のブロックがMLP(FFN)処理にそれぞれ対応します。右側がSwitch Transformerの処理を表しており、複数のFFNをExpertと見なし、Routerでtokenを各Expertに割り当てる処理が導入されています。
このような処理を行うことで同一レイヤーに複数のMLP処理が存在することから計算コストは上げずにパラメータ数を増やすことが可能になります。以下、詳しい処理についてSwitch Transformers論文の数式を元に確認を行います。
Mixture of Expert Routing
Switch Transformerの論文ではtokenのベクトル表現を$\mathbf{x} \in d_{model}$とおくとき、全$N$個のExpertsの中で$i$番目のExpertのgate-valueの$p_{i}(\mathbf{x})$が下記のように定義されます。
$$
\large
\begin{align}
p_{i}(\mathbf{x}) &= \frac{e^{h_{i}(\mathbf{x})}}{\sum_{j=1}^{N} e^{h_{j}(\mathbf{x})}} = \mathrm{Softmax}(h_{i}(\mathbf{x})) \\
h(\mathbf{x}) &= W_{r} \mathbf{x} \\
W_{r} & \in \mathbb{R}^{N \times d_{model}}
\end{align}
$$
上記の$h(\mathbf{x})$は要素数が$N$のベクトルであり、$h_{i}(\mathbf{x})$や$h_{j}(\mathbf{x})$は$h(\mathbf{x})$の$i$番目の要素と$j$番目の要素にそれぞれ対応します。
一般的なMixture of ExpertにおけるRoutingでは、このように計算を行ったgate-valueの$p_{1}(\mathbf{x}), \cdots , p_{N}(\mathbf{x})$の中から上位$k$個の値のインデックスを選び各Expertの出力の線形和によって全体の出力を得ます。ここで上位$k$個に対応するインデックスの集合を$\mathcal{T}$とおくと、全体の出力$\mathbf{y} \in \mathbb{R}^{d_{model}}$は下記のような式で定義されます。
$$
\large
\begin{align}
\mathbf{y} &= \sum_{i \in \mathcal{T}} p_{i}(\mathbf{x}) E_{i}(\mathbf{x}) \\
E_{i}(\mathbf{x}) &= FFN_{i}(\mathbf{x})
\end{align}
$$
上記の$E_{i}(\mathbf{x})$は各Expertの出力に対応するので、$\mathbf{x}$に$i$番目のExpertのMLP処理を施したと理解すると良いです。
Switch Routing
MoE(Mixture of Experts)論文では前項の「Mixture of Expert Routing」のように複数のExpertを用いて処理を行うことが必須であるとされた一方で、Switch Transformerでは$1$つのトークンに対し$1$つのExpertのみが用いられます。
Switch Transformer論文では$k=1$のExpertを用いるRoutingの方針に基づいて構成されるレイヤーを「Switch Layer」、このようなRoutingを「Switch Routing」のようにそれぞれ表されます。
分散処理とauxiliary loss
Expert CapacityとCapacity Factor
Switch Transformerでは前節で確認を行ったようにRouterがExperts(複数のFFNに対応)に処理を分岐させます。したがって、各Expertの処理は分散処理が可能です。
一方で単に処理を分岐させるだけの場合、$1$つのExpertに処理が偏り結果的にRouterの処理の意義がなくなる懸念があります。このような場合の対処にあたって、Switch Transformerでは各Expertに下記の数式に基づいて「Expert Capacity」が設定されます。
$$
\large
\begin{align}
\mathrm{expert \,\, capacity} = \left( \frac{\mathrm{tokens \,\, per \,\, batch}}{\mathrm{number \,\, of \,\, experts}} \right) \times \mathrm{capacity \,\, factor}
\end{align}
$$
上記の$\mathrm{tokens \,\, per \,\, batch}$はSwitch Transformerに入力するバッチのトークンの数、$\mathrm{number \,\, of \,\, experts}$はExpertsの数にそれぞれ対応します。
要するに基本的には各Expertに均等に処理を分岐させる前提でExpertの容量の上限が定義され、$\mathrm{capacity \,\, factor}$は生じうる分岐の偏りに対するバッファと解釈すると良いです。
各Expertの容量の上限であるExpert Capacityの数をトークンが超えた場合は超えた分のトークンの計算がその層ではスキップされます。ここまでに確認した内容について論文では下記のような図で図式化されます。
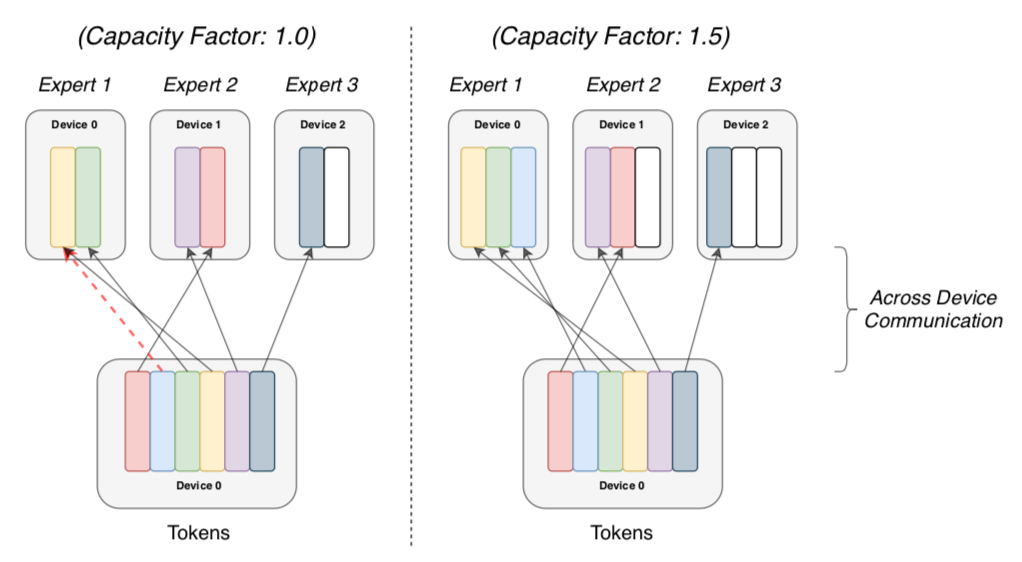
上図のようにSwitch Transformerでは各Expertにトークンを分岐させFFN処理を行います。
図の左のCapacity Factorが$1.0$の場合にExpert Capacityの上限がオーバーし処理されないトークンが出たことが、赤の点線より確認できます。
Load Balancing Loss
それぞれのExpertになるべく均等にtokenが配分されるように、Switch TransformerではLoad Balancing Lossというlossが導入されます。lossの式を下記で表しました。
$$
\large
\begin{align}
\mathrm{loss} &= \alpha N \sum_{i=1}^{N} f_{i} P_{i} \\
f_{i} &= \frac{1}{T} \sum_{x \in \mathcal{B}} \mathbb{1} \{ \mathrm{argmax} \, p(x) = i \} \\
P_{i} &= \frac{1}{T} \sum_{x \in \mathcal{B}} p_{i}(x)
\end{align}
$$
上記は『Switch Routingに用いられる$1$hot表現の平均$(f_{1}, \cdots , f_{N})$と、一般的なMixture of Expert Routingに用いられる確率(gated-value)の平均$(P_{1}, \cdots , P_{N})$の分布が大きく乖離しないようにlossを導入した』と解釈すると良いです。
$N$のより具体的な解釈にあたっては、$f_{1}, \cdots , f_{N}$と$P_{1}, \cdots , P_{N}$の分布がどちらも一様分布の場合、$\displaystyle N \sum_{i=1}^{N} f_{i} P_{i}$が下記のように計算できることを確認しておくと良いと思います。
$$
\large
\begin{align}
N \sum_{i=1}^{N} f_{i} P_{i} &= N \sum_{i=1}^{N} \frac{1}{N} \cdot \frac{1}{N} \\
&= \cancel{N^{2}} \cdot \frac{1}{\cancel{N^{2}}} \\
&= 1
\end{align}
$$
全体処理とパラメータ
参考
・Transformer論文:Attention is All you need[2017]
・Switch Transformer論文
・Mixture of Experts論文
