統計検定準$1$級対応の公式テキストである「統計学実践ワークブック」を$1$章から順に演習問題を中心に解説していきます。
今回は第$5$章「離散型分布」です。
本章のポイント
$4$章までで確率変数や確率密度関数について扱ってきました。本章では、離散型確率変数が従う確率分布である「離散型分布」の代表的なものが紹介されています。
確率分布は扱いたい問題に合わせて様々なものが作られてきました。離散型分布では特に、「ベルヌーイ分布」、「二項分布」、「ポアソン分布」が実用上よく使われています(実用の観点からはこれらの分布が扱いやすいからといった理由が主かもしれませんが)。また、これらの分布は互いに関連があり、ベルヌーイ分布を起点にそれぞれ導出することができます。
確率分布の性質を把握するために、確率変数の値の範囲を確認し(これは定義されている)、期待値と分散を導出してみると良いと思います。また、乱数を生成してヒストグラムを描いてみるのも役立ちますね。
ベルヌーイ分布
「離散型確率分布の数式まとめ」の「ベルヌーイ分布」で詳しく取り扱いました。
二項分布
「離散型確率分布の数式まとめ」の「二項分布」で詳しく取り扱いました。
演習問題解説
問5.1
ウィルスを研究するある研究機関がある。多くのウィルスを検査して滅多に現れないウィルスAを発見することが目的である。今、検査するウィルスが$n$株あり、それぞれのウィルス検査は独立行われ、ウィルスAの発見率は$p$で一定であるとする。
$(1)$ $n$株のウィルスの中にウィルスAが少なくとも$1$株は見つかる確率$\beta$を求めよ
一定確率$p$で独立に$n$回行われる試行に対して、$k$回事象が発生する場合の$k$は二項分布$\mathrm{Bin}(k | p, n)$に従います。本問は、二項分布を利用すれば良いことがわかります。
ウィルスAが少なくとも一つは見つかる確率は、$n$株の中からウィルスAが一つも見つからない場合を$1.0$から引いたものとなります。つまり
$$
\beta = 1.0 – \mathrm{Bin}(k=0 | p, n)
$$
です。
ということで、二項分布の定義に従って素直に計算します。
$$
\begin{align}
\beta &= 1.0 – \mathrm{Bin}(k=0 | p, n) \\
&= 1.0 – \frac{n!}{k! (n-k)!}p^k(1-p)^{n-k} \\
&= 1.0 – \frac{n!}{n!} (1-p)^n = 1-(1-p)^n
\end{align}
$$
$(2)$ Aの発見率$p=1/5000, β=0.98$のときの$n$の値を求めよ
テキストには近似値として次の値が与えられています。
- $\log(1-p) \simeq -p$
- $\log(0.02) \simeq -3.9$
$(1)$で$\beta$を導出していますので、これを単純に展開するだけです。
$$
\begin{align}
\beta = 1-(1-p)^n &= 0.98 \\
(1-p)^n &= 0.02 \\
n \log (1-p) &= \log 0.02 \\
n &= \frac{\log 0.02}{\log (1-p)} \\
n &\simeq \frac{-3.9}{- \frac{1}{5000}} \\
n &\simeq 19500
\end{align}
$$
$4$行目から$5$行目で問に設定されている近似値を代入しています。
問5.2
ある町に住む$40$代前半の男女$79$人を無作為に選び、就業者と非就業者の数を集計した(集計テーブル自体はここでは掲載しません。テキストを参照ください)。
集計の結果、男性で就業者の人数は$40$人であった。
$79$人から$25$人をランダムに選ぶ時、男性で就業者の人数$X$の確率関数を求めよ
この問は、集計の設定から、男性/女性と就業者/非就業者の$4$区分に分けられます。しかし、具体的な問では、男性で就業者の人数$X$について問われているため、$4$区分を$X$の区分とその他の区分と二つに分けて考えます。このように考えますと、$X$は超幾何分布$\mathrm{HG}(N, M, n)$に従うとわかります。
$$
\begin{align}
p(X=x) &= \mathrm(HG)(x | N=79, M=40, n=25) \\
&= \frac{_mC_x \cdot _{N-M}C_{n-x}}{_nC_n} = \frac{ _{40}C_x \cdot _{39}C_{25-x} }{_{79}C_{25}}
\end{align}
$$
問5.3
ある$9$人のグループ($N=9$)のうち、関東地方出身者は$3$人($R=3$)、関東地方以外の出身者は6人だった。このグループから無作為非復元抽出で$4$人を抽出したとする。
$i$番目の人が関東地方出身であるか否かを確率変数とする($X_i = \{0, 1\} (i=1,2,3,4)$)。$X_i=1$とは、$i$番目の人が関東地方出身であることを示す。
$(1)$ $E[X^2_i]$を求めよ
期待値の定義通りに書き下してみます。
$$
E[X^2_i] = \sum_x x^2 p(X_i=x) = (x=1)p(X_i=1) + (x=0)p(X_i=0) = p(X_i=1)
$$
$X_i$は$0$か$1$をとる確率変数なので、期待値を計算するためには$0$と$1$の場合の和になります。ここで、$X_i=0$の場合には$0$となるため、$p(X_i=1)$を導出すればよいことがわかります(上式)。
では、$p(X_i=1)$を考えます。$N$人の中から$n$人を無作為抽出するパターンの数は$_NP_n$となります。このパターン数を全体として、$i$番目が関東出身者であるパターン数を考えれば良いわけです。$i$番目が特定の人(関東出身者$3$人のうちの一人)になるパターン数は、$i$番目が固定されているので、$(N-1)$個から$(n-1)$個を抽出するパターン数ということになります($_{N-1}P_{n-1}$)。関東出身者は$R=3$人おり、$i$番目に入る「特定の人」はこの$3$人のうち誰でも良いわけです。なので、「$i$番目が関東出身者であるパターン数」は$R \cdot _{N-1}P_{n-1}$となります。
以上をまとめて計算すると以下のようになります。
$$
\begin{align}
p(X_i=1) &= \frac{R \cdot _{N-1}P_{n-1}}{_NP_n} \\
&= \frac{3 \cdot _{9-1}P_{4-1}}{_9P_4} = \frac{1}{3}
\end{align}
$$
$(2)$ $X_i, X_j, i \neq j$に対して、$E[X_i X_j]$を求めよ
上記$(1)$と同じ考え方で導出できます。
まずは、期待値の定義通りに展開して、どのような確率を出せば良いのかを考えます。
$$
\begin{align}
E[X_i X_j] &= \sum_i \sum_j x_i x_j p(X_i=x_i, X_j=x_j) \\
&= p(X_i=1, X_j=1)
\end{align}
$$
二つの確率変数の積なので、$x_i = x_j = 1$以外は全て$0$となります。そのため、$p(X_i=1, X_j=1)$を考えれば良いことがわかります。
$i$番目と$j$番目が共に関東出身者であるパターンを考えることになるため、$2$枠が固定されます。そのため、$(N-2)$個から$(n-1)$個を抽出するパターン数ということで$_{N-2}P_{n-2}$パターンあります。この$2$枠の取り方として、関東出身者は$4$人いるので、$_4P_2$パターンあります。全てのパターン数は$(1)$と同じなので、結局以下のようになります。
$$
\begin{align}
E[X_i X_j] &= p(X_i=1, X_j=1) \\
&= \frac{_RP_2 \cdot _{N-2}P_{n-2}}{_NP_n} \\
&= \frac{_4P_2 \cdot _{9-2}P_{4-2}}{_9P_4} = \frac{1}{12}
\end{align}
$$
$(3)$ 標本平均の分散$V[\bar{X}]$を求めよ
$V[\bar{X}]$を展開します。
$$
\begin{align}
V[\bar{X}] &= V\left[ \frac{1}{4} \sum X_i \right] = \frac{1}{16}V\left[ \sum X_i \right]
\end{align}
$$
非独立な確率変数の和の分散は以下のようになります。
$$
V\left[ \sum_i X_i \right] = \sum_i V\left[ X_i \right] + \sum_{i \neq j} \mathrm{Cov}(X_i, X_j)
$$
分散を期待値で書き下すと以下の通り(参考)となり、$(1)$の結果を適用して分散を算出しておきます。
$$
\begin{align}
V[X] &= E[X^2] – (E[X])^2 \\
&= \frac{1}{3} – \left(\frac{1}{3} \right)^2 = \frac{2}{9}
\end{align}
$$
また、共分散$\mathrm{Cov}(X_i, X_j)$は以下のように展開できます。こちらも$(1)$、$(2)$の結果を利用して算出しておきます。
$$
\begin{align}
\mathrm{Cov}(X_i, X_j) &= E[X_iX_j] – E[X_i]E[X_j] \\
&= \frac{1}{12} – \frac{1}{3}\frac{1}{3} = – \frac{1}{36}
\end{align}
$$
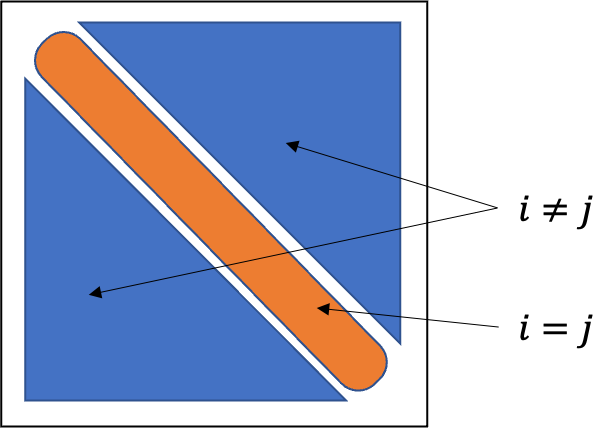
共分散は$i, j$の組み合わせ分足し合わせる必要がありますが、組み合わせ数はここでは$12$通りとなります。分散共分散行列を考えた際の非対角成分が$i \neq j$要素となります。今回は確率変数が$4$つなので、$16$通りから$4$通りを引いて$12$通りであることがわかります(下図参照)。$_4P_2$を考えても同じなのでわかりやすい方で考えてもらえたらと思います。
以上をまとめると標本平均の分散は以下の通りです。
$$
\begin{align}
V[\bar{X}] &= V\left[ \frac{1}{4} \sum X_i \right] = \frac{1}{16}V\left[ \sum X_i \right] \\
&= \frac{1}{16} \left\{ \sum_i V\left[ X_i \right] + \sum_{i \neq j} \mathrm{Cov}(X_i, X_j) \right\} \\
&= \frac{1}{16} \left\{ 4\frac{2}{9} + 12 \left(- \frac{1}{36} \right) \right\} = \frac{5}{144}
\end{align}
$$
問5.4
サッカーの試合において、チーム$T1$があげた得点($X$)とチーム$T2$があげた得点($Y$)がそれぞれ独立にポアソン分布に従うと仮定する。ポアソン分布のパラメータは以下の通り。
$$
\begin{align}
X &\sim \mathrm{Poi}(X | \lambda_1=1.5) \\
Y &\sim \mathrm{Poi}(X | \lambda_2=3.0)
\end{align}
$$
二つのチームの合計得点が従う分布の平均と分散を求めよ
ポアソン分布に従う確率変数の和の確率分布は、パラメータが二つのポアソン分布のパラメータの和となるポアソン分布になります(ポアソン分布の再生成)。
$$
X+Y \sim \mathrm{Poi}(\lambda_1 + \lambda_2)
$$
また、ポアソン分布の期待値と分散は共に同じで、ポアソン分布のパラメータと同じとなります。
以上のことから、平均が$4.5$、分散が$4.5$のポアソン分布に従うということがわかります。
合計得点が$5$点という条件のもとで、$T1$の得点$X$の従う分布を求めよ
条件付き分布を計算します。計算上のポイントとして、$X$と$Y$はそれぞれ独立であると示されているので、同時分布が単純な積になります。
$$
\begin{align}
p(X=x | x+y=5) &= \frac{p(x, x+y=5)}{p(x+y=5)} = \frac{p(x, y=5-x)}{p(x+y=5)} \\
&= \frac{p(x) p(y=5-x)}{p(x+y=5)} \\
&= \frac{\mathrm{Poi}(x|\lambda_1) \mathrm{Poi}(y=5-x|\lambda_2) }{\mathrm{Poi}(x+y=5|\lambda = \lambda_1 + \lambda_2)}
\end{align}
$$
上述の通り、同時分布が単純な形になるところ以外は定義通りです。
ポアソン分布は$\mathrm{Poi}(y|\lambda) = \frac{\lambda^{y}}{y!} e^{-\lambda}$なので、これを代入して愚直に計算していけば条件付き分布を導出することができます。
$$
\begin{align}
p(X=x | x+y=5) &= \frac{\mathrm{Poi}(x|\lambda_1) \mathrm{Poi}(y=5-x|\lambda_2) }{\mathrm{Poi}(x+y=5|\lambda = \lambda_1 + \lambda_2)} \\
&= \frac{\frac{\lambda_1^{x}}{x!} e^{-\lambda_1} \frac{\lambda_2^{5-x}}{(5-x)!} e^{-\lambda_2} }{ \frac{(\lambda_1+\lambda_2)^{5}}{5!} e^{-(\lambda_1+\lambda_2)} } \\
&= \frac{5! \lambda_1^{x} \lambda_2^{5-x}}{ x! (5-x)! (\lambda_1 + \lambda_2)^5 } \\
\end{align}
$$
ここまでの展開結果を眺めてみると、$\lambda_i$に関係しない部分と関係する部分に分割して考えてみると見覚えのある形が見えてきそうな気配がします。まず、$\lambda_i$に関係しない部分を整理すると以下のように二項係数が出てきます。
$$
\frac{5!}{x! (5-x)!} = \binom{5}{k} = _5C_x
$$
次に、$\lambda$に関係する項ですが、これも展開すると以下の通りとなります。
$$
\begin{align}
\frac{\lambda_1^{x} \lambda_2^{5-x}}{ (\lambda_1 + \lambda_2)^5 } &= \left( \frac{\lambda_1}{\lambda_1+\lambda_2} \right)^x \left( \frac{\lambda_2}{\lambda_1+\lambda_2} \right)^{5-x} \\
&= \left( \frac{\lambda_1}{\lambda_1+\lambda_2} \right)^x \left( 1 – \frac{\lambda_1}{\lambda_1+\lambda_2} \right)^{5-x}
\end{align}
$$
$(\lambda_1 + \lambda_2)^5 = (\lambda_1 + \lambda_2)^x(\lambda_1 + \lambda_2)^{5-x}$と分解できることが注意点です。$x+y=5$で$x, y$共に$0$以上の整数なので、$x \lt 5$であることは明らかです。
ここまで来れば明らかに、上記の条件付き分布は二項分布になることがわかります。
$$
\begin{align}
p(X=x | x+y=5) &= \binom{5}{k}\left( \frac{\lambda_1}{\lambda_1+\lambda_2} \right)^x \left( 1 – \frac{\lambda_1}{\lambda_1+\lambda_2} \right)^{5-x} \\
&= \mathrm{Bin}(x | \theta=\frac{\lambda_1}{\lambda_1+\lambda_2}, n=5)
\end{align}
$$
問5.5
シールがおまけとして入っているお菓子がある。シールは全部で$4$種類で全て等確率とする。
$(1)$ $4$種類全てのカードを揃えるまでに必要な購入回数の期待値を求めよ
持っていないシールが出るまでの回数$x$は、シールの種類が含まれる確率を$p$で等確率とすると以下の幾何分布に従います。
$$
\mathrm{Geo}(x | p) = p(1-p)^{x-1}
$$
ここで、持っているシールの種類数を$m$、シールの全種類数を$k$とおくと、持っていない種類のシールが出てくる確率$p_m$は以下の通りとなります。
$$
p_m = \frac{1}{k}(k-m)
$$
既に持っているシールが$m$種類ある場合に、持っていない種類のシールが出る回数を示す確率変数を$X_m$とすると、$k=4$種類全てのカードを揃えるまでに必要な回数の期待値は、$m$を$0 \sim (k-1)$までとした確率変数$X_m$の和の期待値を導出すれば良いわけです。
$$
\begin{align}
E[X] = \sum^{k-1}_{m=0} E[X_m]
\end{align}
$$
ここで、$X_m$は上記の通り幾何分布に従います。幾何分布に従う確率変数の期待値は次の通りです。
$$
E[X] = \frac{1}{p}
$$
幾何分布の期待値の導出は確率母関数を利用すると容易に導出できます。
以上を利用して、期待値を導出します。
$$
\begin{align}
E[X] &= \sum^{k-1}_{m=0} E[X_m] = \sum^{k-1}_{m=0} \frac{k}{k-m} \\
&= \frac{4}{4} + \frac{4}{3} + \frac{4}{2} + \frac{4}{1} = \frac{25}{3}
\end{align}
$$
$(2)$ シールの種類が追加された場合の購入回数の期待値について
テキストに書かれている問いの内容をかいつまんで記載すると次の通りとなります。
$4$種類のシールを集め切った後に、シールが$1$種類追加された。
初めの$4$種類と追加された$1$種類の計$5$枚のシールを集めきるまでの購入回数の期待値を$x$とする。一方、初めから$5$種類のシールがあったときに$5$種類のシールを集め切るまでの試行回数の期待値を$y$とする。
では、$x-y$を求めよ。
とされています。まずは$x, y$それぞれを導出します。
$x$については、$(1)$の結果を利用し、幾何分布に従う確率変数の期待値を単純に足し合わせれば良いだけです。
$$
x = \frac{25}{3} + \frac{1}{p_5} = \frac{25}{3} + \frac{5}{1} = \frac{40}{3}
$$
ここで、$5$種類のカードのうち$4$種類のカードが既に手元にあって、$5$種類目のカードが出る確率は$\displaystyle p_5 = \frac{1}{5}$となります($(1)$参照)。
次に$y$については、$(1)$の計算を$k$を変更して再計算するだけです。
$$
\begin{align}
y &= \sum^{5-1}_{m=0} \frac{5}{5-m} \\
&= \frac{5}{5} + \frac{5}{4} + \frac{5}{3} + \frac{5}{2} + \frac{5}{1} = \frac{137}{12}
\end{align}
$$
以上の結果を利用して$x-y$は以下の通りです。
$$
x-y = \frac{40}{3} – \frac{137}{12} = \frac{23}{12}
$$
参考文献
ワークブック以外の参考資料として以下のものがおすすめです。
- 松原ら, 統計学入門, $1991$, 東京大学出版会
- 矢島ら, 自然科学の統計学, $1992$, 東京大学出版会