群内分散と群間分散の比の最大化からフィッシャーの線形判別の導出について確認する

フィッシャーの線形判別については所々で出てくる一方で、途中計算が省略されるケースも多い。当稿では可能な限り明示的に導出を行うことで、理解しやすい内容になるように試みるものとする。
「パターン認識と機械学習(PRML)」の上巻の$4.1.4$節の導出が比較的わかりやすいので、主にこちらを参考に確認を行う。

前提の確認

内積と正射影

$D$次元のベクトルの$\mathbf{x}_n$と$\mathbf{w}$を考える。それぞれ下記のように表すことができる。
$$
\begin{align}
\mathbf{x}_n &= \left(\begin{array}{c} x_{n1} \\ \vdots \\ x_{nD} \end{array} \right) \\
\mathbf{w} &= \left(\begin{array}{c} w_1 \\ \vdots \\ w_D \end{array} \right)
\end{align}
$$
上記を用いて本論のフィッシャーの線形判別では$\mathbf{x}_n$をサンプル、$\mathbf{w}$を変数のように取り扱う任意のベクトルとし、最適化の指標を設けて$\mathbf{w}$に関して基準値を最大にするように最適化問題を解く。そのため、$\mathbf{x}_n$で表した際の$n$はサンプルのインデックスであると考えればよい。

上記のように$D$次元のベクトルの$\mathbf{x}_n$と$\mathbf{w}$を定義した際に、$\mathbf{x}_n$から$\mathbf{w}$への射影を行うことを考える。これは内積を計算することで求めることができる。

$$
\begin{align}
\mathbf{w}^{\mathrm{T}}\mathbf{x}_n &= \left(\begin{array}{r} w_1 & … & w_D \end{array} \right) \left(\begin{array}{c} x_{n1} \\ \vdots \\ x_{nD} \end{array} \right)
\end{align}
$$

フィッシャーの線形判別

問題設定

$2$クラス分類問題を考える。クラス$C_1$に属するサンプルが$N_1$個、クラス$C_2$に属するサンプルが$N_2$個と考える。また、サンプルは$D$次元ベクトルの$\mathbf{x}_n$と表すこととする。
このとき、下記のように各クラスに含まれるサンプルの平均ベクトルの$\mathbf{m}_1$と$\mathbf{m}_2$を計算する。
$$
\begin{align}
\mathbf{m}_1 &= \frac{1}{N_1} \sum_{n \in C_1} \mathbf{x}_n \\
\mathbf{m}_2 &= \frac{1}{N_2} \sum_{n \in C_2} \mathbf{x}_n
\end{align}
$$

ここで$\mathbf{m}_1$は$N_1$個のサンプルの平均、$\mathbf{m}_2$は$N_2$個のサンプルの平均となる。この時にそれぞれのクラスの平均ベクトルをベクトル$\mathbf{w}$への射影は下記のように表すことができる。
$$
\begin{align}
m_1 &= \mathbf{w}^{\mathrm{T}} \mathbf{m}_1 \\
m_2 &= \mathbf{w}^{\mathrm{T}} \mathbf{m}_2
\end{align}
$$

上記において$m_1$と$m_2$はそれぞれ$\mathbf{w}$への$\mathbf{m}_1$と$\mathbf{m}_2$の射影であると考えることができる。またここで、$\mathbf{w}$は大きさよりも向きに意味があるので、$\displaystyle \mathbf{w}^{\mathrm{T}}\mathbf{w} = \sum_{i=1}^{D} w_i^2=1$という制約を設けることとする。

ここまでに定義した内容を元に、クラス分類を行うにあたっての射影先のベクトル$\mathbf{w}$について考える。

シンプルな解法

$$
\begin{align}
m_2-m_1 = \mathbf{w}^{\mathrm{T}} (\mathbf{m}_2-\mathbf{m}_1) \cdot \cdot \cdot (1)
\end{align}
$$

一番シンプルな考え方は上記を最大化する$\mathbf{w}$を求めることである。$\displaystyle \mathbf{w}^{\mathrm{T}}\mathbf{w} = \sum_{i=1}^{D} w_i^2=1$の制約の元で、$(1)$が最大となる$\mathbf{w}$を求めるにあたっては、ラグランジュの未定乗数法に基づいて、下記の最大値問題を解けば良い。
$$
\begin{align}
L(\mathbf{w}, \lambda) &= m_2-m_1 + \lambda(1-\mathbf{w}^{\mathrm{T}}\mathbf{w}) \\
&= \mathbf{w}^{\mathrm{T}} (\mathbf{m}_2-\mathbf{m}_1) + \lambda(1-\mathbf{w}^{\mathrm{T}}\mathbf{w})
\end{align}
$$
上記を$\mathbf{w}$と$\lambda$に関して微分すると下記のようになる。
$$
\begin{align}
\frac{\partial L(\mathbf{w}, \lambda)}{\partial \mathbf{w}} &= \mathbf{m}_2-\mathbf{m}_1 – 2\lambda \mathbf{w} \\
\frac{\partial L(\mathbf{w}, \lambda)}{\partial \lambda} &= 1-\mathbf{w}^{\mathrm{T}}\mathbf{w}
\end{align}
$$
上記がそれぞれ$0$に等しいので、ここから下記のような条件が得られる。
$$
\begin{align}
\frac{\partial L(\mathbf{w}, \lambda)}{\partial \mathbf{w}} &= 0 \\
\mathbf{m}_2-\mathbf{m}_1 – 2\lambda \mathbf{w} &= 0 \\
\mathbf{m}_2-\mathbf{m}_1 &= 2\lambda \mathbf{w}
\end{align}
$$
$$
\begin{align}
\frac{\partial L(\mathbf{w}, \lambda)}{\partial \lambda} &= 0 \\
1-\mathbf{w}^{\mathrm{T}}\mathbf{w} &= 0 \\
\mathbf{w}^{\mathrm{T}}\mathbf{w} &= 1
\end{align}
$$
上記より、$\mathbf{m}_2-\mathbf{m}_1$と$\mathbf{w}$が平行であれば、$\displaystyle \mathbf{w}^{\mathrm{T}}\mathbf{w} =1$の制約の元で、(1)が最大となる。

よって、$\mathbf{w} \propto \mathbf{m}_2-\mathbf{m}_1$と$\mathbf{w}^{\mathrm{T}}\mathbf{w}=1$を満たす$\mathbf{w}$がここで求める$\mathbf{w}$となる。

フィッシャーの線形判別

シンプルな解法は数式がシンプルで解きやすい一方で、各クラスの共分散によってはうまく分類できないケースがある。下記で示した”Pattern Recognition and Machine Learning”のFigure4.6の左の図ような場合は単にそれぞれのクラスからの平均ベクトルを取るだけでは誤分類が多くなる。

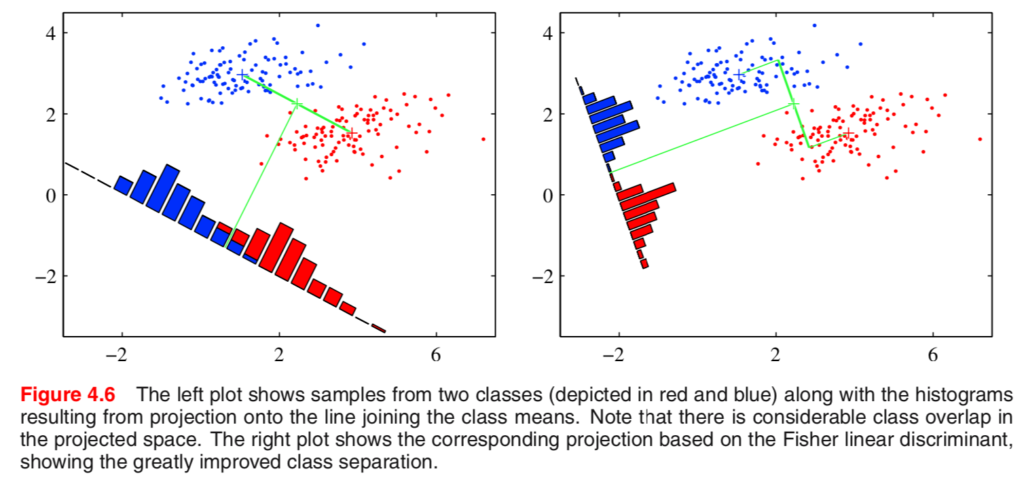
この課題の解決にあたってよく用いられるのが上図の右の図で表されたフィッシャーの線形判別である。フィッシャーの線形判別は単に平均ベクトルからの射影が大きくなる$\mathbf{w}$ではなく、射影したベクトルにおいてそれぞれのクラス内の分散が小さくなるようにするような$\mathbf{w}$を求めるべきだという考え方である。具体的にはクラス間の分散とクラス内の分散の比を目的関数とした最適化を行う。
以下ではクラス内分散$V_W$($W$は”within-class”を意味する)とクラス間分散$V_B$($B$は”between-class”を意味する)の比を$\displaystyle J(\mathbf{w}) = \frac{V_B}{V_W}$の最大化について考える。ここで$V_W$と$V_B$はそれぞれ下記のように表すことができる。
$$
\begin{align}
V_W &= \sum_{n \in C_1} (y_n-m_1)^2 + \sum_{n \in C_2} (y_n-m_2)^2 \\
&= \sum_{n \in C_1} (\mathbf{w}^{\mathrm{T}}\mathbf{x}_n-\mathbf{w}^{T}\mathbf{m}_1)^2 + \sum_{n \in C_2} (\mathbf{w}^{\mathrm{T}}\mathbf{x}_n-\mathbf{w}^{T}\mathbf{m}_2)^2 \\
&= \sum_{n \in C_1} (\mathbf{w}^{\mathrm{T}}(\mathbf{x}_n-\mathbf{m}_1))^2 + \sum_{n \in C_2} (\mathbf{w}^{\mathrm{T}}(\mathbf{x}_n-\mathbf{m}_2))^2 \\
&= \sum_{n \in C_1} \mathbf{w}^{\mathrm{T}}(\mathbf{x}_n-\mathbf{m}_1)(\mathbf{x}_n-\mathbf{m}_1)^{\mathrm{T}}\mathbf{w} + \sum_{n \in C_2} \mathbf{w}^{\mathrm{T}}(\mathbf{x}_n-\mathbf{m}_2)(\mathbf{x}_n-\mathbf{m}_2)^{\mathrm{T}}\mathbf{w} \\
&= \mathbf{w}^{\mathrm{T}}\left(\sum_{n \in C_1}(\mathbf{x}_n-\mathbf{m}_1)(\mathbf{x}_n-\mathbf{m}_1)^{\mathrm{T}}+\sum_{n \in C_2} (\mathbf{x}_n-\mathbf{m}_2)(\mathbf{x}_n-\mathbf{m}_2)^{\mathrm{T}}\right)\mathbf{w} \\
&= \mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w} \\
V_B &= (m_2-m_1)^2 \\
&= (\mathbf{w}^{\mathrm{T}} (\mathbf{m}_2-\mathbf{m}_1))^2 \\
&= \mathbf{w}^{\mathrm{T}}(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^{\mathrm{T}}\mathbf{w} \\
&= \mathbf{w}^{\mathrm{T}}\mathbf{S}_B\mathbf{w}
\end{align}
$$
途中計算において成分表示までは行わなかったが、成分表示も行えば下記の導出に類似する。
https://www.hello-statisticians.com/explain-terms-cat/pca1.html
また、途中計算において下記のように$\mathbf{S}_W$と$\mathbf{S}_B$を定義した。
$$
\begin{align}
\mathbf{S}_W &= \sum_{n \in C_1}(\mathbf{x}_n-\mathbf{m}_1)(\mathbf{x}_n-\mathbf{m}_1)^{\mathrm{T}}+\sum_{n \in C_2} (\mathbf{x}_n-\mathbf{m}_2)(\mathbf{x}_n-\mathbf{m}_2)^{\mathrm{T}} \\
\mathbf{S}_B &= (\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^{\mathrm{T}} \cdot \cdot \cdot (2)
\end{align}
$$

よって$J(\mathbf{w})$は下記のように表せる。
$$
\begin{align}
J(\mathbf{w}) &= \frac{V_B}{V_W} \\
&= \frac{\mathbf{w}^{\mathrm{T}}\mathbf{S}_B\mathbf{w}}{\mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w}}
\end{align}
$$
ここで$J(\mathbf{w})$を最大にする$\mathbf{w}$を考えるにあたって、$J(\mathbf{w})$の微分を考える。
$$
\begin{align}
\frac{\partial J(\mathbf{w})}{\partial \mathbf{w}} = \frac{2\mathbf{S}_B\mathbf{w}(\mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w}) – 2(\mathbf{w}^{\mathrm{T}}\mathbf{S}_B\mathbf{w})\mathbf{S}_W\mathbf{w}}{(\mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w})^2}
\end{align}
$$
上記において$\mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w}$と$\mathbf{w}^{\mathrm{T}}\mathbf{S}_B\mathbf{w}$は単なるスカラーのため、式の形ほど複雑な計算とはならないことに注意しておくとよい。ここで$\displaystyle \frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}$が$0$となる場合は下記が成立する。
$$
\begin{align}
\mathbf{S}_B\mathbf{w}(\mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w}) &= (\mathbf{w}^{\mathrm{T}}\mathbf{S}_B\mathbf{w})\mathbf{S}_W\mathbf{w} \\
(\mathbf{w}^{\mathrm{T}}\mathbf{S}_B\mathbf{w})\mathbf{S}_W\mathbf{w} &= \mathbf{S}_B\mathbf{w}(\mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w}) \\
(\mathbf{w}^{\mathrm{T}}\mathbf{S}_B\mathbf{w})\mathbf{S}_W\mathbf{w} &= (\mathbf{w}^{\mathrm{T}}\mathbf{S}_W\mathbf{w})\mathbf{S}_B\mathbf{w}
\end{align}
$$
ここで$(2)$より$\mathbf{S}_B\mathbf{w}$は$(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^{\mathrm{T}}\mathbf{w}$となるが、$(\mathbf{m}_2-\mathbf{m}_1)^{\mathrm{T}}\mathbf{w}$がスカラーとなるため、$\mathbf{S}_B\mathbf{w}$は$\mathbf{m}_2-\mathbf{m}_1$に平行なベクトルとなる。よって、$\mathbf{w}$の満たす条件は下記となる。
$$
\begin{align}
\mathbf{w} \propto \mathbf{S}_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)
\end{align}
$$

$S_W$と$S_B$の解釈

前項では$S_W$と$S_B$について唐突に定義された印象があるが、前項で導出された$\mathbf{w} \propto \mathbf{S}_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$の解釈を行うにあたって、$S_W$の解釈が必要となり、それに関連して$S_B$も抑えておくと良いと思われる。

前項でクラス内分散$V_W$とクラス間分散$V_B$について定義したが、$S_W$と$S_B$はそれぞれに対応する分散共分散行列である。
https://www.hello-statisticians.com/explain-terms-cat/pca1.html#i-6
分散共分散行列が出てくることについては、基本的には上記の議論を参考に理解すればよい。が、大元の$V_W$と$V_B$の定義が少々基本的な分散の定義とは異なっているため、一般的な分散共分散行列と完全に同じではないことには注意しておくとよい。

$$
\begin{align}
S_W = \sum_{n \in C_1}(\mathbf{x}_n-\mathbf{m}_1)(\mathbf{x}_n-\mathbf{m}_1)^{\mathrm{T}}+\sum_{n \in C_2} (\mathbf{x}_n-\mathbf{m}_2)(\mathbf{x}_n-\mathbf{m}_2)^{\mathrm{T}}
\end{align}
$$
まず上記で表した$S_W$は二つのクラス内において、それぞれクラスの平均ベクトルを元に分散を計算している。クラス内においては一般的な分散共分散行列ではあるが、その和を計算していることに注意が必要である。ここで、サンプル数で割らないのは一般的な分散共分散行列とは異なるが、$J(\mathbf{w})$の最大化にあたって重要なのは向きであり、大きさではないことを考えて割らないと考えればよいと思われる。また、サンプル数で割らないことによって、サンプル数に基づいた重み付け和を考えていることになり、重み付け平均と同様な意味を持ち、サンプル数が多いクラスの分散共分散行列をより参考にすると考えれば良さそうである。

$$
\begin{align}
S_B &= (\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^{\mathrm{T}}
\end{align}
$$
$S_B$はクラス間の分散に対応する分散共分散行列とされるが、二つのベクトルの差の二乗を計算しており、平均からの差の二乗和を計算していないことが一般的な分散の数式と異なるように見える。が、二値における分散を計算すると、二つの差の二乗のスカラー倍が分散となることも合わせて抑えておくとよい。
$$
\begin{align}
\left( m_1 – \frac{m_1+m_2}{2} \right)^2 + \left( m_2 – \frac{m_1+m_2}{2} \right)^2 &= \left( \frac{m_2-m_1}{2} \right)^2 + \left( \frac{m_1-m_2}{2} \right)^2 \\
&= \frac{(m_2-m_1)^2}{4} + \frac{(m_2-m_1)^2}{4} \\
&= \frac{(m_2-m_1)^2}{2} \\
&= \frac{1}{2}V_B
\end{align}
$$
上記に基づいて$S_B$が導出されるため、こちらも向きの最適化を考えるにあたってはスカラー倍は考えなくて良いのであれば、この定義で十分である。

$\mathbf{w} \propto \mathbf{S}_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$の図形的解釈

https://www.hello-statisticians.com/explain-terms-cat/linear_discriminant1.html#i-6
上記で結果の図示が取り扱われているが、数式$\mathbf{w} \propto \mathbf{S}_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$の図形的解釈について明示的に議論されるケースが少ないため、ここでまとめることとする。

前項の$S_W$を考えるにあたって、二つのクラスの分散共分散行列が等しいと考える方がイメージがつかみやすいので、以下そのように考えるとする。
$$
\begin{align}
S_W = \left(\begin{array}{cc} 1 & 0.7 \\ 0.7 & 1 \end{array} \right)
\end{align}
$$
たとえば上記のような分散共分散行列$S_W$に基づいて考えるにあたって、上記の固有値は$(1-\lambda)^2-0.7^2=0$より、$\lambda=1.7, 0.3$、対応する大きさ$1$の固有ベクトルは$\displaystyle \left(\begin{array}{c} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right), \left(\begin{array}{c} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right)$となる。

https://www.hello-statisticians.com/explain-terms-cat/multi_norm_dist1.html#i-9
https://www.hello-statisticians.com/explain-terms-cat/multi_norm_dist1.html#i-10
この時の$S_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$の解釈は固有ベクトルを$\mathbf{u}_i$のようにおき、上記を参考にすることで理解することができる。
$$
\begin{align} S_W^{-1}(\mathbf{m}_2-\mathbf{m}_1) = \sum_{i=1}^{D} \frac{1}{\lambda_i} \mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{m}_2-\mathbf{m}_1)
\end{align}
$$
この式において、$\mathbf{u}_i^{\mathrm{T}} (\mathbf{m}_2-\mathbf{m}_1)$は$(\mathbf{m}_2-\mathbf{m}_1)$の$\mathbf{u}_i$への正射影であり、スカラー値となる。よって、$\mathbf{u}_i \mathbf{u}_i^{\mathrm{T}} (\mathbf{m}_2-\mathbf{m}_1)$の向きは$\mathbf{u}_i$となる。

要するに$S_W$の固有ベクトルの$\displaystyle \frac{\mathbf{u}_i^{\mathrm{T}} (\mathbf{m}_2-\mathbf{m}_1)}{\lambda_i}$倍の重み付け和を求めることで、$\mathbf{w}$の向きを求めるというのがフィッシャーの線形判別である。ここで、$(\mathbf{m}_2-\mathbf{m}_1)$と平行な固有ベクトル$\mathbf{u}_i$がある場合、他の固有ベクトルは$(\mathbf{m}_2-\mathbf{m}_1)$と直交するため、$(\mathbf{m}_2-\mathbf{m}_1)$と平行な固有ベクトル$\mathbf{u}_i$が$\mathbf{w}$の向きになると考えるとわかりやすい。またこの時、前述のように二つのクラスそれぞれに関しての分散共分散行列が等しいと考えるなら、それぞれのクラスの固有ベクトルの向きと$\mathbf{w}$の向きが一致すると考えるとイメージしやすい。

まとめ

行列計算がなかなか複雑なため、ある程度ベクトルを用いた微分については慣れておくとよいと思います。