統計検定1級の2018年11月の「統計応用、人文科学」の問2の解答例と解説について取り扱いました。他の問題の解答に関しては下記よりご確認ください。
https://www.hello-statisticians.com/stat_certifi_1_app
問題
詳しくは統計検定公式よりご確認ください。
解答
$[1]$
分散がそれぞれ$20$、共分散が$14$であるので、相関係数は$14/\sqrt{20}^2=0.7$のように計算できる。
$[2]$
$U_A^2=U_B^2$より、判別境界線$U$の方程式は下記のように得られる。
$$
\large
\begin{align}
U_A^2 &= U_B^2 \\
(x_1-30)^2 + (x_2-50)^2 &= (x_1-40)^2 + (x_2-50)^2 \\
(x_1-30)^2 &= (x_1-40)^2 \\
x_1^2 – 60x_1 + 900 &= x_1^2 – 80x_2 + 1600 \\
20x_1 &= 700 \\
x_1 &= 35
\end{align}
$$
これにより、$a$はA、$b, c$はBに分類されることがわかる。
$[3]$
下記を実行することで境界線$U$と境界線$M$に関してそれぞれ描画を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
r1, r2 = np.array([1., 3., 5.]), np.array([1., 4., 7.])
theta = np.linspace(0,2*np.pi,50)
x1, x2, y1, y2 = np.zeros([50,3]), np.zeros([50,3]), np.zeros([50,3]), np.zeros([50,3])
for i in range(x1.shape[1]):
x1[:,i], y1[:,i] = r1[i]*np.cos(theta), r1[i]*np.sin(theta)
x2[:,i], y2[:,i] = r2[i]*np.cos(theta), r2[i]*np.sin(theta)
plt.subplot(2,1,1)
for i in range(x1.shape[1]):
plt.plot(x1[:,i]+30,y1[:,i]+50,"g--")
plt.plot(x1[:,i]+40,y1[:,i]+50,"b--")
plt.plot(np.zeros(100)+35,np.linspace(42,58,100),"k--")
plt.subplot(2,1,2)
Sigma = np.array([[1.,0.7],[0.7,1.]])
lamb, U_T = linalg.eig(Sigma,right=True)
for i in range(x2.shape[1]):
vec = np.array([np.sqrt(lamb[0])*x2[:,i],np.sqrt(lamb[1])*y2[:,i]])
vec_transformed = np.dot(U_T,vec)
plt.plot(vec_transformed[0,:]+30,vec_transformed[1,:]+50,"g--")
plt.plot(vec_transformed[0,:]+40,vec_transformed[1,:]+50,"b--")
plt.plot(np.linspace(25,42,100),10.*np.linspace(25,42,100)/7.,"k--")
plt.show()・実行結果
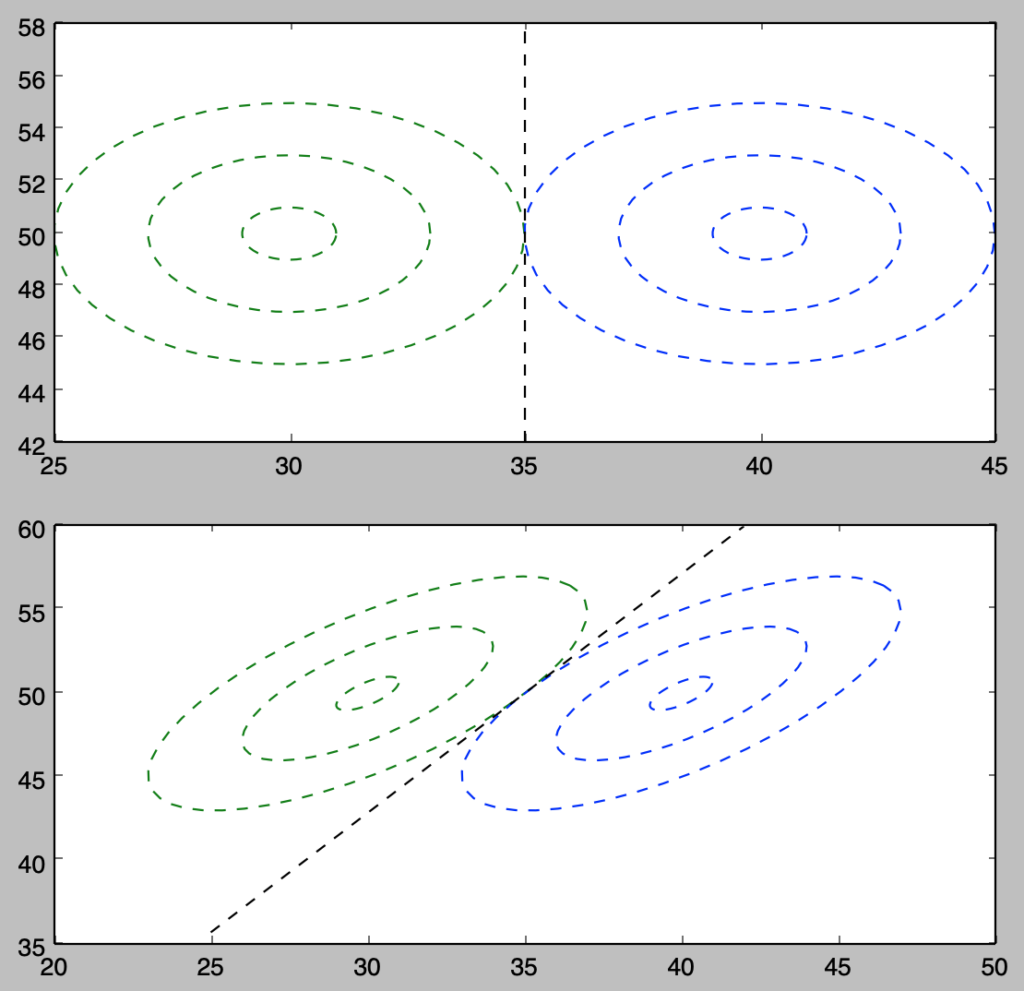
2つあるうちのの下の方の図が境界線$M$に対応するが、これに基づいて$a,b,c$は$a,b$が$A$、$c$が$B
$にそれぞれ分類されることがわかる。
$[4]$
省略
解説
線形判別に関しては下記でも取り扱いましたので、下記も参考にしてみてください。
