主成分分析が分散共分散行列の固有値・固有ベクトルで得られることを確認する

多次元のベクトルから主要なベクトルを構築する主成分分析は分散共分散行列の固有値・固有ベクトルを用いて導出できることが知られている。とはいえ、関連の数式を確認すると、二次形式が出てくることでなかなか導出が難しい。
そこで本稿では関連の導出を可能な限り数式変形を追いやすいようにまとめるものとする。導出にあたっては「パターン認識と機械学習(PRML)」の下巻の$12$章の導出が詳しいので、こちらの記載を元に数式変形を追いやすいように所々改変する。

前提知識

固有値・固有ベクトルの導出

下記などで詳しく取り扱った。

行列の基本事項まとめ 〜$2$次元正方行列の積、行列式、逆行列、固有値・固有ベクトル、対角化〜

べき乗法・逆反復法の概要とQR法・逆反復法を用いた固有値・固有ベクトルの数値計算

分散共分散行列の概要

行列$\mathbf{S}$の$(i,i)$成分を$i$番目の変数$x_i$の分散、$(i,j)$成分を$i$番目の変数$x_i$と$j$番目の変数$x_j$の共分散でそれぞれ表す場合、$\mathbf{S}$を分散共分散行列という。

ラグランジュの未定乗数法

制約条件ありの最適化問題(定義域の条件がある最大値問題)を解くにあたって、よく用いられるのがラグランジュの未定乗数法である。具体例を元に考える方がわかりやすいので、以下の問題を解くことを考えることとする。
$$
\begin{align}
\mathrm{maximize} &: f(x_1, x_2) = x_1+x_2 \\
\mathrm{constraint} &: x_1^2+x_2^2 = 1
\end{align}
$$
上記は高校数学の数Ⅱでも見かける問題であり、下図を利用して解くことができる。

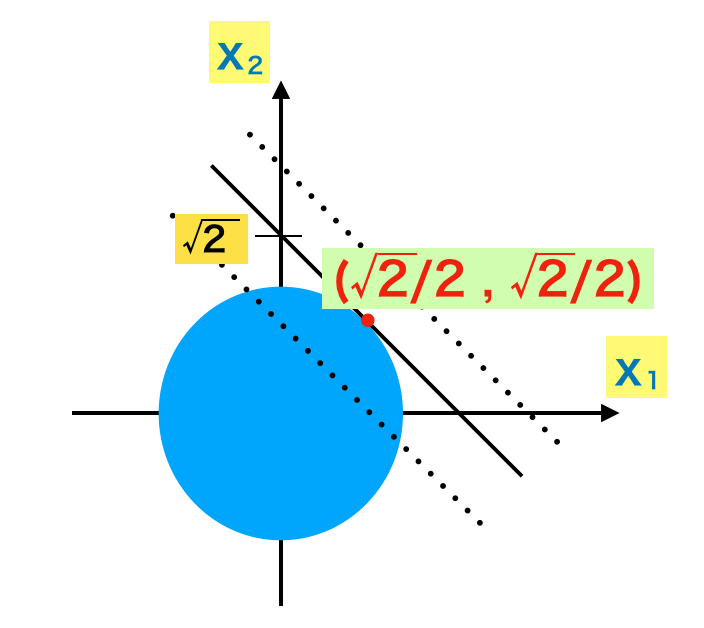
図のように考えることで、$x_2=-x_1+k$で考えた直線が$x_1^2+x_2^2 = 1$を通る際の、$k$が最大値となる$x_1$と$x_2$を求めることで制約付き最適化問題を解くことができる。この問題においては$\displaystyle (x_1,x_2) = \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)$がここでの解となる。

ここまでで確認した解法を用いることで、高校レベルの数学のトピックを元に問題を解くことができる一方で、もう少し複雑な関数に対して計算を行うにあたって毎回図を描いて考えるのは大変である。このような時にラグランジュの未定乗数法が役に立つ。
$$
\begin{align}
\mathrm{maximize}: f(x_1, x_2, \lambda) = x_1+x_2+\lambda(1-(x_1^2+x_2^2))
\end{align}
$$
ラグランジュの未定乗数法では上記のように関数をおき、$f(x_1, x_2, \lambda)$を最大にする$x_1,x_2,\lambda$を求める手法である。ここで、それぞれを変数とみなし偏微分を計算すると下記のようになる。
$$
\begin{align}
\frac{\partial f(x_1, x_2, \lambda)}{\partial x_1} &= 1 – 2 \lambda x_1 \\
\frac{\partial f(x_1, x_2, \lambda)}{\partial x_2} &= 1 – 2 \lambda x_2 \\
\frac{\partial f(x_1, x_2, \lambda)}{\partial \lambda} &= 1 – (x_1^2 + x_2^2)
\end{align}
$$
ここで、上記が全て$0$となるような$x_1,x_2,\lambda$を求める。

$\displaystyle x_1 = \frac{1}{2 \lambda}$、$\displaystyle x_2 = \frac{1}{2 \lambda}$を$1 – (x_1^2 + x_2^2)=0$に代入し、$\displaystyle \lambda = \frac{1}{\sqrt{2}}$が求められる。
またこれを$\displaystyle x_1 = \frac{1}{2 \lambda}$、$\displaystyle x_2 = \frac{1}{2 \lambda}$に代入することで、$\displaystyle x_1 = \frac{\sqrt{2}}{2}$、$\displaystyle x_2 = \frac{\sqrt{2}}{2}$を得ることができ、これは図を用いて得た結果と一致する。

このようにラグランジュの未定乗数法を用いることで、制約ありの最適化問題を解くにあたって一関数の最大値問題のみを考えれば良くなり、導出が行いやすくなる。

二次形式とベクトル(二乗和をベクトルと行列で表す)

二次形式(quadratic form)は変数に関する次数が$2$の多項式である。たとえば$x_1$と$x_2$を変数とした時、下記は二次形式である。
$$
\begin{align}
ax_1^2 + bx_1 &x_2 + cx_2^2 \\
(abc &\neq 0)
\end{align}
$$
二次形式には様々な式の形があるが、主成分分析や回帰分析など統計に関連する計算においては二乗和を行列表記に変換することが多い。
$$
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i1} + w_2 x_{i2})^2
\end{align}
$$
以下では、上記の二乗和の変形に関する代表的なパターンのみ紹介する。
$$
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i1} + w_2 x_{i2})^2 &= (w_1 x_{11} + w_2 x_{12})^2 + \cdots + (w_1 x_{n1} + w_2 x_{n2})^2 \\
&= \left(\begin{array}{r} w_1x_{11} + w_1x_{12} & \cdots & w_1x_{n1} + w_1x_{n2} \end{array} \right) \left(\begin{array}{c} w_1x_{11} + w_1x_{12} \\ \vdots \\ w_1x_{n1} + w_1x_{n2} \end{array} \right) \\
&= \left(\begin{array}{r} w_1 & w_2 \end{array} \right) \left(\begin{array}{rr} x_{11} & \cdots & x_{n1} \\ x_{12} & \cdots & x_{n2} \end{array} \right) \left(\begin{array}{cc} x_{11} & x_{12} \\ \vdots & \vdots \\ x_{n1} & x_{n2} \end{array} \right) \left(\begin{array}{c} w_1 \\ w_2 \end{array} \right) \\
&= \left(\begin{array}{r} w_1 & w_2 \end{array} \right) \left(\begin{array}{cc} \displaystyle \sum_{i=1}^{n} x_{i1}^2 & \displaystyle \sum_{i=1}^{n} x_{i1}x_{i2} \\ \displaystyle \sum_{i=1}^{n} x_{i2}x_{i1} & \displaystyle \sum_{i=1}^{n} x_{i2}^2 \end{array} \right) \left(\begin{array}{c} w_1 \\ w_2 \end{array} \right) \cdot \cdot \cdot (a)
\end{align}
$$
上記のような計算を行うことで二乗和を$\mathbf{w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\mathbf{X}\mathbf{w}$のような計算式で表すことが可能となる。これを元に回帰分析の最小二乗法の式を解くと正規方程式が得られるし、$\mathbf{X}$を平均からの差で置き換えることで$\mathbf{X}^{\mathrm{T}}\mathbf{X}$が分散共分散行列に変形でき本稿のテーマである主成分分析の導出にも活用できる。

ここで一番注意が必要なのが、$(a)$がスカラーであることである。変形前の左辺を見ればスカラーであることが自明ではあるものの、行列の変形を多く行ううちに行列のように考えがちでそうなると議論がわからなくなるため、この辺はなるべく注意しておくと良い。

スカラー関数をベクトルで微分する($\nabla$)

最適化問題は数学的には最大値問題に帰着することが多い。そのため、大概の問題において前項で表したような二次形式に関して微分を行い最大値問題や最小値問題を解くことが試みられる。この時に多変数のスカラー関数の偏微分を行うと考えることもできるが、式の形が複雑な場合などはベクトル表記のまま微分することもある。

ベクトル表記に基づく微分は行なっていること自体は偏微分と変わらないものの、変形にあたって通常の関数の微分のように詳細の計算は記述されないことが多いため、別途抑えておく必要がある。
$$
\begin{align}
\mathbf{w} = \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right)
\end{align}
$$

本項では上記で表した$p$次元ベクトル$\mathbf{w}$でスカラー関数を微分することを考える。微分にあたっては下記のように演算子を定めるとする。
$$
\begin{align}
\nabla = \frac{\partial}{\partial \mathbf{w}} = \left(\begin{array}{c} \frac{\partial}{\partial w_1} \\ \vdots \\ \frac{\partial}{\partial w_p} \end{array} \right)
\end{align}
$$

この時、$\nabla (w_1+w_2+w_3+…+w_p)$は下記のように全ての要素が$1$の$p$次元ベクトルに一致する。
$$
\begin{align}
\nabla (w_1+w_2+w_3+…+w_p) &= \frac{\partial}{\partial \mathbf{w}}(w_1+w_2+w_3+…+w_p) \\
&= \left(\begin{array}{c} \frac{\partial}{\partial w_1} \\ \vdots \\ \frac{\partial}{\partial w_p} \end{array} \right)(w_1+w_2+w_3+…+w_p) \\
&= \left(\begin{array}{c} 1 \\ \vdots \\ 1 \end{array} \right)
\end{align}
$$

次に$p$次元ベクトル$\mathbf{x}$を導入し、内積(行列の積の演算で表記するが、$1$行$p$列×$p$行$1$列の行列の積は内積と変わらないのでここではあえて内積と表記した)をベクトルで微分することを考える。
$$
\begin{align}
\mathbf{x} = \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right)
\end{align}
$$

ここで$\mathbf{x}$は上記のように定義する。この時内積は下記の二通りで表記できる。
$$
\begin{align}
\mathbf{x}^{\mathrm{T}}\mathbf{w} &= \left(\begin{array}{r} x_1 & \cdots & x_p \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
\mathbf{w}^{\mathrm{T}}\mathbf{x} &= \left(\begin{array}{r} w_1 & \cdots & w_p \end{array} \right) \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right)
\end{align}
$$

上記のスカラー関数(内積はスカラー関数)に対して、下記のように$\mathbf{w}$で微分を行うことができる。
$$
\begin{align}
\nabla \mathbf{x}^{\mathrm{T}}\mathbf{w} &= \nabla \left(\begin{array}{r} x_1 & … & x_p \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= \nabla (x_1w_1+x_2w_2+…x_pw_p) \\
&= \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right) \\
&= \mathbf{x} \\
\nabla \mathbf{w}^{\mathrm{T}}\mathbf{x} &= \left(\begin{array}{r} w_1 & … & w_p \end{array} \right) \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right) \\
&= \nabla (w_1x_1+w_2x_2+…w_px_p) \\
&= \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right) \\
&= \mathbf{x}
\end{align}
$$
上記のように計算結果はどちらも$\mathbf{x}$となる。

次は$\mathbf{w}^{\mathrm{T}}\mathbf{w}$の微分について考える。下記のように微分を行うことができる。
$$
\begin{align}
\nabla \mathbf{w}^{\mathrm{T}}\mathbf{w} &= \nabla \left(\begin{array}{r} w_1 & … & w_p \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= \nabla (w_1^2+w_2^2+…w_p^2) \\
&= 2\left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= 2\mathbf{w}
\end{align}
$$
途中で出てきたスカラー関数は$\mathbf{w}$の二次式のため、この計算は二次形式のベクトルでの微分と考えて良い。

次は$\mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w}$の微分について考える。ここで$A$は下記のように定義する。
$$
\begin{align}
\mathbf{A} = \left(\begin{array}{rrr} a_{11} & .. & a_{1p} \\ .. & .. & .. \\ a_{p1} & .. & a_{pp} \end{array} \right)
\end{align}
$$

以下、$\mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w}$を$\mathbf{w}$で微分する。
$$
\begin{align}
\nabla \mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w} &= \nabla \left(\begin{array}{r} w_1 & … & w_p \end{array} \right) \left(\begin{array}{rrr} a_{11} & .. & a_{1p} \\ .. & .. & .. \\ a_{p1} & .. & a_{pp} \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= \nabla \left(\begin{array}{r} w_1 & … & w_p \end{array} \right) \left(\begin{array}{c} w_1a_{11}+..+w_pa_{1p} \\ \vdots \\ w_1a_{p1}+..+w_pa_{pp} \end{array} \right) \\
&= \nabla \left( w_1(w_1a_{11}+..+w_pa_{1p})+…+w_p(w_1a_{p1}+..+w_pa_{pp}) \right) \\
&= \left(\begin{array}{c} 2a_{11}w_1+..+(a_{1p}+a_{p1})w_p \\ \vdots \\ (a_{p1}+a_{1p})w_1+..+2a_{pp}w_p \end{array} \right) \\
&= \left(\begin{array}{ccc} 2a_{11} & .. & (a_{1p}+a_{p1}) \\ .. & .. & .. \\ (a_{p1}+a_{1p}) & .. & 2a_{pp} \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= (\mathbf{A}+\mathbf{A}^{\mathrm{T}})\mathbf{w}
\end{align}
$$

ここで$\mathbf{A}^{\mathrm{T}}$は$\mathbf{A}$の転置行列であり、$\mathbf{A}$が対称行列であれば$\nabla \mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w} = 2\mathbf{A}\mathbf{w}$となり、これは一般的な二次式の微分と同様の形になる。

また、前項で確認した$\mathbf{w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\mathbf{X}\mathbf{w}$の$\mathbf{X}^{\mathrm{T}}\mathbf{X}$は対称行列となるので、$\nabla \mathbf{w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\mathbf{X}\mathbf{w} = 2\mathbf{X}^{\mathrm{T}}\mathbf{X}\mathbf{w}$となる。前項では$\mathbf{X}$を$n$行$2$列と考えたが、$n$行$p$列としても対称行列となるため、$\nabla \mathbf{w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\mathbf{X}\mathbf{w} = 2\mathbf{X}^{\mathrm{T}}\mathbf{X}\mathbf{w}$はp次元の$\mathbf{w}$に関して成立する。

主成分分析の導出

以下では主成分が分散共分散行列の固有ベクトルを計算することで得られることを確認する。まず、「主成分とは何を指すべきか」という定義から確認する。主成分は「二次元以上のサンプルが与えられた際に、分散を最大にする方向である」と考えることで一般的に定義される。

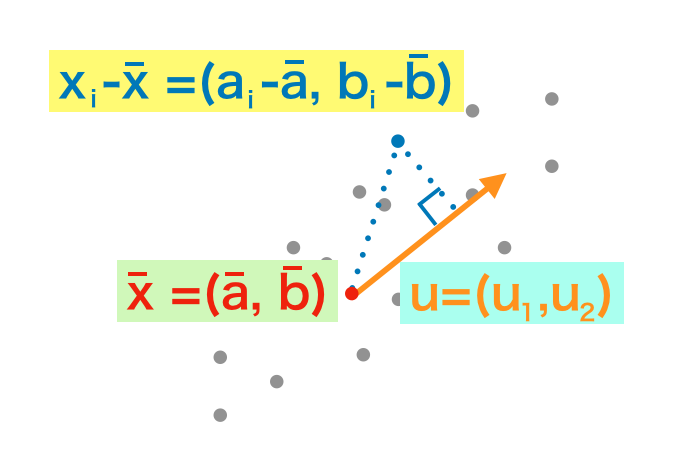
要するに上図におけるオレンジのベクトルの方向が主成分であるとイメージしておくとよい。ここでこの定義から「オレンジのベクトルが分散共分散行列の固有ベクトルで与えられること」が導出できれば、「主成分は分散共分散行列の固有ベクトルを求めることで得られる」とすることができる。

ここでは議論の簡易化のために総数$n$の$i$番目のサンプルが$2$次元ベクトル$\displaystyle \mathbf{x}_i = \left(\begin{array}{c} a_i \\ b_i \end{array} \right)$で得られることとする。また、サンプルの平均ベクトルが$\displaystyle \mathbf{\bar{x}} = \left(\begin{array}{c} \bar{a} \\ \bar{b} \end{array} \right)$で得られることとする。$3$次元以上についても基本的には同様に考えることができるので、一般的な議論と同様に考えておけば良い。このとき単位ベクトル$\displaystyle \mathbf{u} = \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right)$を考えると、サンプルの平均ベクトルを始点とするサンプルのベクトル$\mathbf{x}_i-\mathbf{\bar{x}}$から単位ベクトル$\mathbf{u}$への正射影を考えると下記のように計算することができる。
$$
\begin{align}
(\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}) \mathbf{u} &= (a_i-\bar{a})u_1 + (b_i-\bar{b})u_2 \cdot \cdot \cdot (1)
\end{align}
$$

上記の左辺は内積と同様であるので、$\displaystyle (\mathbf{x}_i-\mathbf{\bar{x}}) \cdot \mathbf{u}$と表すこともできる。また、左辺で使われている文字がベクトルであるのに対して、右辺で使われている文字は単なるスカラー(数)であることは注意しておきたい。

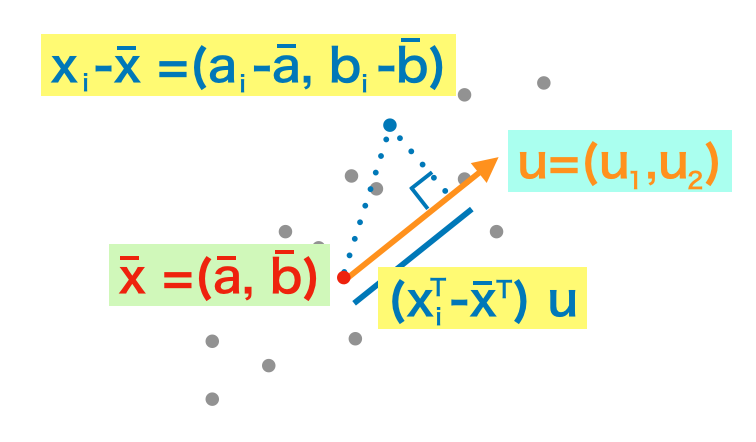
ここで$(1)$式は単位ベクトル$\displaystyle \mathbf{u} = \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right)$に$\mathbf{x}_i-\mathbf{\bar{x}}$を射影したベクトルであり、上図の青の線の長さに相当する。これに基づいて$\mathbf{x}_i^{\mathrm{T}} \mathbf{u}$の分散$\displaystyle \frac{1}{n} \sum_{i=1}^{n}(\mathbf{x}_i^{\mathrm{T}}\mathbf{u}-\mathbf{\bar{x}}^{\mathrm{T}}\mathbf{u})^2 = \frac{1}{n} \sum_{i=1}^{n}((\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}) \mathbf{u})^2$を計算すると下記のようになる。
$$
\begin{align}
\frac{1}{n} \sum_{i=1}^{n}((\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}) \mathbf{u})^2 &= \frac{1}{n}\sum_{i=1}^{n}((a_i-\bar{a})u_1 + (b_i-\bar{b})u_2)^2 \\
&= \frac{1}{n} \left(\begin{array}{r} (a_1-\bar{a})u_1 + (b_1-\bar{b})u_2 & … & (a_n-\bar{a})u_1 + (b_n-\bar{b})u_2 \end{array} \right) \left(\begin{array}{c} (a_1-\bar{a})u_1 + (b_1-\bar{b})u_2 \\ \vdots \\ (a_n-\bar{a})u_1 + (b_n-\bar{b})u_2 \end{array} \right) \\
&= \frac{1}{n} \left(\begin{array}{r} u_1 & u_2 \end{array} \right) \left(\begin{array}{rr} a_1-\bar{a} & … & a_n-\bar{a} \\ b_1-\bar{b} & … & b_n-\bar{b} \end{array} \right) \left(\begin{array}{cc} a_1-\bar{a} & b_1-\bar{b} \\ \vdots & \vdots \\ a_n-\bar{a} & b_n-\bar{b} \end{array} \right) \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right) \\
&= \frac{1}{n} \left(\begin{array}{r} u_1 & u_2 \end{array} \right) \left(\begin{array}{rr} \displaystyle \sum_{i=1}^{n}(a_i-\bar{a})(a_i-\bar{a}) & \displaystyle \sum_{i=1}^{n}(a_i-\bar{a})(b_i-\bar{b}) \\ \displaystyle \sum_{i=1}^{n}(b_i-\bar{b})(a_i-\bar{a}) & \displaystyle \sum_{i=1}^{n}(b_i-\bar{b})(b_i-\bar{b}) \end{array} \right) \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right) \\
&= \left(\begin{array}{r} u_1 & u_2 \end{array} \right) \left(\begin{array}{rr} \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(b_i-\bar{b}) \\ \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(b_i-\bar{b}) \end{array} \right) \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right) \cdot \cdot \cdot (2)
\end{align}
$$

ここで$(2)$式において、$\left(\begin{array}{r} u_1 & u_2 \end{array} \right)$と$\displaystyle \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right)$の間の行列は数式よりサンプル$\mathbf{x}_1, \mathbf{x}_2, …, \mathbf{x}_n$の分散共分散行列であることがわかる。$2$変数で考えたため、分散共分散行列が$2$行$2$列となったことも着目しておくとよい。この分散共分散行列を$\mathbf{S}$とおくことにする。

ここでここまでに導出した$\mathbf{u}^{\mathrm{T}}\mathbf{S}\mathbf{u}$を$\mathbf{u}$が単位ベクトルであるという制約条件の下で最大化することを考える。$\mathbf{u}$が単位ベクトルであることは$\mathbf{u}^{\mathrm{T}}\mathbf{u} = u_1^2+u_2^2 = 1^2 = 1$が成立することに等しい。これによりラグランジュの未定乗数法より下記を最大化する$\mathbf{u}$を求める問題となる。
$$
\begin{align}
\mathbf{u}^{\mathrm{T}}\mathbf{S}\mathbf{u} + \lambda(1-\mathbf{u}^{\mathrm{T}}\mathbf{u})
\end{align}
$$

上記の$\mathbf{u}$に関する微分が$0$ベクトル$\mathbf{0}$になる際の$\mathbf{u}$の満たす条件を計算すると下記のようになる。（必要十分条件というより、必要条件と考えて議論を進めていることに注意。）
$$
\begin{align}
2\mathbf{S}\mathbf{u} – &2\lambda\mathbf{u} = \mathbf{0} \\
\mathbf{S}\mathbf{u} &= \lambda\mathbf{u} \cdot \cdot \cdot (3)
\end{align}
$$

上記は分散共分散行列$\mathbf{S}$に関する固有値・固有ベクトルに関する式となる。またこのとき$(3)$式の両辺に左から$\mathbf{u}^{\mathrm{T}}$をかけることを考える。
$$
\begin{align}
\mathbf{u}^{\mathrm{T}}\mathbf{S}\mathbf{u} = \lambda\mathbf{u}^{\mathrm{T}}\mathbf{u}
\end{align}
$$

上記において、固有値$\lambda$はスカラーなので順番を入れ替えることができた。また、前述のように$\mathbf{u}$が単位ベクトルなので$\mathbf{u}^{\mathrm{T}}\mathbf{u} = 1$が成立する。よって、$\lambda$は下記のように表せる。
$$
\begin{align}
\lambda = \mathbf{u}^{\mathrm{T}}\mathbf{S}\mathbf{u}
\end{align}
$$
上記を$(2)$式と見比べることで、分散共分散行列$\mathbf{S}$の固有値$\lambda$は分散の値を表していることがわかる。このとき、固有ベクトルの中から固有値$\lambda$を最大にするベクトルを選べばこれが第1主成分となる。

まとめ

$\mathbf{S}\mathbf{u} = \lambda\mathbf{u}$や$\mathbf{u}^{\mathrm{T}}\mathbf{S}\mathbf{u}$の導出が書籍などの記載では省略されることが多いので、なるべく導出の流れがわかりやすいように記載を行いました。
少々難しい式変形ではありますが、線形回帰のパラメータを導出する際の正規方程式を解くときにも似たような式変形を行うので、可能な限り抑えておくと良いです。どうしても難しい際も$2$次元で表記することで大体のイメージはつかめるので、何度か導出を追って把握すると良いのではと思います。

↓演習問題
https://www.hello-statisticians.com/practice/stat_practice9.html

参考

• 【主成分分析の導出 # 01】主成分分析とはどんなものか？実装を通して雰囲気をつかむ（YouTube）