下記などで取り扱った、主成分分析(PCA; Principal Component Analysis)に関する問題演習を通した理解ができるように問題・解答・解説をそれぞれ作成しました。
・標準演習$100$選
https://www.hello-statisticians.com/practice_100
Contents
基本問題
二次形式の和を行列の積で表記する
・問題
二次形式(quadratic form)は変数に関する次数が2の多項式である。
$$
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i1} + w_2 x_{i2})^2
\end{align}
$$
具体的には上記も二次形式だが、二乗和の取り扱いは統計に関する多くの導出で出てくるので、シンプルに取り扱えると導出や考察にあたってのアドバンテージが取れる。
以下、下記の問題に答えよ。
i) $\displaystyle \sum_{i=1}^{n} (w_1 x_{i1} + w_2 x_{i2})^2$を$\displaystyle \sum$を用いないで表せ。
ⅱ) $\displaystyle \sum_{i=1}^{n} x_i^2$を下記のように定義される$\mathbf{x}$を用いて表せ。
$$
\begin{align}
\mathbf{x} = \left(\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right)
\end{align}
$$
ⅲ) $\displaystyle \sum_{i=1}^{n} (w_1 x_{i1} + w_2 x_{i2})^2$が下記のように変形できることを確認せよ。
$$
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i2} + w_2 x_{i2})^2 = \left(\begin{array}{cc} w_1 & w_2 \end{array} \right) \left(\begin{array}{ccc} x_{11} & \cdots & x_{n1} \\ x_{12} & \cdots & x_{n2} \end{array} \right) \left(\begin{array}{cc} x_{11} & x_{12} \\ \vdots & \vdots \\ x_{n1} & x_{n2} \end{array} \right) \left(\begin{array}{c} w_1 \\ w_2 \end{array} \right)
\end{align}
$$
iv) ⅲ)を参考に$\displaystyle \sum_{i=1}^{n} (w_1 x_{i1} + w_2 x_{i2})^2$が下記のように変形できることを確認せよ。
$$
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i2} + w_2 x_{i2})^2 = \left(\begin{array}{cc} w_1 & w_2 \end{array} \right) \left(\begin{array}{cc} \displaystyle \sum_{i=1}^{n} x_{i1}^2 & \displaystyle \sum_{i=1}^{n} x_{i1}x_{i2} \\ \displaystyle \sum_{i=1}^{n} x_{i2}x_{i1} & \displaystyle \sum_{i=1}^{n} x_{i2}^2 \end{array} \right) \left(\begin{array}{c} w_1 \\ w_2 \end{array} \right)
\end{align}
$$
v) iv)の結果において、$\displaystyle \left(\begin{array}{cc} \displaystyle \sum_{i=1}^{n} x_{i1}^2 & \displaystyle \sum_{i=1}^{n} x_{i1}x_{i2} \\ \displaystyle \sum_{i=1}^{n} x_{i2}x_{i1} & \displaystyle \sum_{i=1}^{n} x_{i2}^2 \end{array} \right)$が対称行列であることを確認せよ。
・解答
i)
$\displaystyle \sum_{i=1}^{n}$の定義に基づき、下記のように表すことができる。
$$
\large
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i1} + w_2 x_{i2})^2 = (w_1 x_{11} + w_2 x_{12})^2 + \cdots + (w_1 x_{n1} + w_2 x_{n2})^2
\end{align}
$$
ⅱ)
下記のように表すことができる。
$$
\large
\begin{align}
\sum_{i=1}^{n} x_i^2 &= x_1^2 + x_2^2 + \cdots + x_n^2 \\
&= \left(\begin{array}{ccc} x_1 & \cdots & x_n \end{array} \right) \left(\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right) \\
&= \mathbf{x}^{T} \mathbf{x}
\end{align}
$$
ⅲ)
下記のように変形できる。
$$
\large
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i2} + w_2 x_{i2})^2 &= (w_1 x_{11} + w_2 x_{12})^2 + \cdots + (w_1 x_{n1} + w_2 x_{n2})^2 \\
&= \left(\begin{array}{ccc} w_1x_{11} + w_1x_{12} & \cdots & w_1x_{n1} + w_1x_{n2} \end{array} \right) \left(\begin{array}{c} w_1x_{11} + w_1x_{12} \\ \vdots \\ w_1x_{n1} + w_1x_{n2} \end{array} \right) \\
&= \left(\begin{array}{cc} w_1 & w_2 \end{array} \right) \left(\begin{array}{ccc} x_{11} & \cdots & x_{n1} \\ x_{12} & \cdots & x_{n2} \end{array} \right) \left(\begin{array}{cc} x_{11} & x_{12} \\ \vdots & \vdots \\ x_{n1} & x_{n2} \end{array} \right) \left(\begin{array}{c} w_1 \\ w_2 \end{array} \right)
\end{align}
$$
iv)
ⅲ)の導出結果において、$\displaystyle \left(\begin{array}{ccc} x_{11} & \cdots & x_{n1} \\ x_{12} & \cdots & x_{n2} \end{array} \right) \left(\begin{array}{cc} x_{11} & x_{12} \\ \vdots & \vdots \\ x_{n1} & x_{n2} \end{array} \right)$を計算することで、下記のように導出することができる。
$$
\large
\begin{align}
\sum_{i=1}^{n} (w_1 x_{i2} + w_2 x_{i2})^2 &= \left(\begin{array}{cc} w_1 & w_2 \end{array} \right) \left(\begin{array}{ccc} x_{11} & \cdots & x_{n1} \\ x_{12} & \cdots & x_{n2} \end{array} \right) \left(\begin{array}{cc} x_{11} & x_{12} \\ \vdots & \vdots \\ x_{n1} & x_{n2} \end{array} \right) \left(\begin{array}{c} w_1 \\ w_2 \end{array} \right) \\
&= \left(\begin{array}{cc} w_1 & w_2 \end{array} \right) \left(\begin{array}{cc} \displaystyle \sum_{i=1}^{n} x_{i1}^2 & \displaystyle \sum_{i=1}^{n} x_{i1}x_{i2} \\ \displaystyle \sum_{i=1}^{n} x_{i2}x_{i1} & \displaystyle \sum_{i=1}^{n} x_{i2}^2 \end{array} \right) \left(\begin{array}{c} w_1 \\ w_2 \end{array} \right)
\end{align}
$$
v)
$\displaystyle \sum_{i=1}^{n} x_{i1}x_{i2} = \sum_{i=1}^{n} x_{i2}x_{i1}$より、対称行列であることが確認できる。
・解説
ここで確認した二乗和をベクトルや行列の積で表す計算は統計学を理解する上で様々なトピックで出てくる話題であるので、何度も確認して慣れておくと良いと思います。
スカラーをベクトルで微分する
・問題
$$
\begin{align}
\nabla = \frac{\partial}{\partial \mathbf{w}} = \left(\begin{array}{c} \displaystyle \frac{\partial}{\partial w_1} \\ \vdots \\ \displaystyle \frac{\partial}{\partial w_p} \end{array} \right)
\end{align}
$$
上記のように微分を表す演算子の$\nabla$を定義する。このとき以下の問題に答えよ。
i) $\nabla (w_1+w_2+w_3+\cdots+w_p)$を求めよ。
ⅱ) 下記のように$\mathbf{w}, \mathbf{x}$が定義されるとき、$\nabla \mathbf{w}^{\mathrm{T}}\mathbf{x}, \nabla \mathbf{x}^{\mathrm{T}}\mathbf{w}$をそれぞれ求めよ。
$$
\begin{align}
\mathbf{w} &= \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right) \\
\mathbf{x} &= \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right)
\end{align}
$$
ⅲ) ⅱ)のように$\mathbf{w}$が表されるとき、$\nabla \mathbf{w}^{\mathrm{T}}\mathbf{w}$を求めよ。
iv) 下記のように$\mathbf{A}$が表されるとき、$\mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w}$を求めよ。
$$
\begin{align}
\mathbf{A} = \left(\begin{array}{ccc} a_{11} & \cdots & a_{1p} \\ \vdots & \ddots & \vdots \\ a_{p1} & \cdots & a_{pp} \end{array} \right)
\end{align}
$$
v) $\nabla \mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w} = (\mathbf{A}+\mathbf{A}^{\mathrm{T}})\mathbf{w}$を導出せよ。
・解答
i)
下記のように導出できる。
$$
\begin{align}
\nabla (w_1+w_2+w_3+\cdots+w_p) &= \frac{\partial}{\partial \mathbf{w}}(w_1+w_2+w_3+\cdots+w_p) \\
&= \left(\begin{array}{c} \displaystyle \frac{\partial}{\partial w_1} \\ \vdots \\ \displaystyle \frac{\partial}{\partial w_p} \end{array} \right)(w_1+w_2+w_3+\cdots+w_p) \\
&= \left(\begin{array}{c} 1 \\ \vdots \\ 1 \end{array} \right)
\end{align}
$$
ⅱ)
下記のようにそれぞれ導出できる。
$$
\begin{align}
\nabla \mathbf{x}^{\mathrm{T}}\mathbf{w} &= \nabla \left(\begin{array}{r} x_1 & \cdots & x_p \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= \nabla (x_1w_1+x_2w_2+\cdots+x_pw_p) \\
&= \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right) \\
&= \mathbf{x} \\
\nabla \mathbf{w}^{\mathrm{T}}\mathbf{x} &= \left(\begin{array}{r} w_1 & \cdots & w_p \end{array} \right) \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right) \\
&= \nabla (w_1x_1+w_2x_2+\cdots+w_px_p) \\
&= \left(\begin{array}{c} x_1 \\ \vdots \\ x_p \end{array} \right) \\
&= \mathbf{x}
\end{align}
$$
ⅲ)
下記のように微分を行うことができる。
$$
\begin{align}
\nabla \mathbf{w}^{\mathrm{T}}\mathbf{w} &= \nabla \left(\begin{array}{r} w_1 & \cdots & w_p \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= \nabla (w_1^2+w_2^2+\cdots+w_p^2) \\
&= 2\left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= 2\mathbf{w}
\end{align}
$$
iv)
下記のように計算できる。
$$
\begin{align}
\mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w} &= \left(\begin{array}{ccc} w_1 & \cdots & w_p \end{array} \right) \left(\begin{array}{ccc} a_{11} & \cdots & a_{1p} \\ \vdots & \ddots & \vdots \\ a_{p1} & \cdots & a_{pp} \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= \left(\begin{array}{ccc} w_1 & \cdots & w_p \end{array} \right) \left(\begin{array}{c} w_1a_{11}+..+w_pa_{1p} \\ \vdots \\ w_1a_{p1}+ \cdots +w_pa_{pp} \end{array} \right) \\
&= \left( w_1(w_1a_{11}+ \cdots +w_pa_{1p})+\cdots+w_p(w_1a_{p1}+ \cdots +w_pa_{pp}) \right)
\end{align}
$$
v)
下記のように微分を行うことができる。
$$
\begin{align}
\nabla \mathbf{w}^{\mathrm{T}}\mathbf{A}\mathbf{w} &= \nabla \left( w_1(w_1a_{11}+\cdots+w_pa_{1p})+\cdots+w_p(w_1a_{p1}+\cdots+w_pa_{pp}) \right) \\
&= \left(\begin{array}{c} 2a_{11}w_1+\cdots+(a_{1p}+a_{p1})w_p \\ \vdots \\ (a_{p1}+a_{1p})w_1+\cdots+2a_{pp}w_p \end{array} \right) \\
&= \left(\begin{array}{ccc} 2a_{11} & \cdots & (a_{1p}+a_{p1}) \\ \vdots & \ddots & \vdots \\ (a_{p1}+a_{1p}) & \cdots & 2a_{pp} \end{array} \right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\
&= (\mathbf{A}+\mathbf{A}^{\mathrm{T}})\mathbf{w}
\end{align}
$$
・解説
i)〜v)のどれもスカラーをベクトルで偏微分すると考えた際の重要な式なので抑えておくと良いです。ⅲ)は正則化の際などにも出てくるし、主成分ベクトルの導出にあたってはv)が現れます。
ラグランジュの未定乗数法
・問題
$$
\begin{align}
\mathrm{maximize} &: \quad f(x_1, x_2) = x_1+x_2 \\
\mathrm{constraint} &: \quad x_1^2+x_2^2 = 1
\end{align}
$$
上記のような制約付き最適化問題があるとする。これはconstraint(制約)が成立する時に$f$を最大にする$x_1, x_2$を求めることを表している。この時、以下の問題に答えよ。
i) $x_1^2+x_2^2 = 1$が円の方程式であることを利用して問題を解け。
ⅱ) ラグランジュの未定乗数法を用いて問題を解け。
・解答
i)
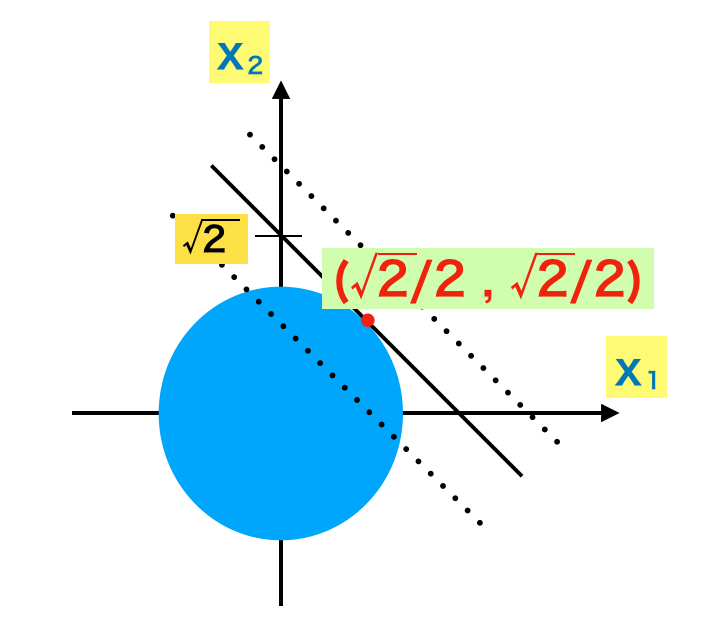
上図のように考えることで、$x_2=-x_1+k$で考えた直線が$x_1^2+x_2^2 = 1$を通る際の、$k$が最大値となる$x_1$と$x_2$を求めることで制約付き最適化問題を解くことができる。この問題においては$\displaystyle (x_1,x_2) = \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)$がここでの解となる。
ⅱ)
$$
\begin{align}
\mathrm{maximize}: \quad f(x_1, x_2, \lambda) = x_1+x_2+\lambda(1-(x_1^2+x_2^2))
\end{align}
$$
ラグランジュの未定乗数法では上記のように関数をおき、$f(x_1, x_2, \lambda)$を最大にする$x_1,x_2,\lambda$を求める手法である。ここで、それぞれを変数とみなし偏微分を計算すると下記のようになる。
$$
\begin{align}
\frac{\partial f(x_1, x_2, \lambda)}{\partial x_1} &= 1 – 2 \lambda x_1 \\
\frac{\partial f(x_1, x_2, \lambda)}{\partial x_2} &= 1 – 2 \lambda x_2 \\
\frac{\partial f(x_1, x_2, \lambda)}{\partial \lambda} &= 1 – (x_1^2 + x_2^2)
\end{align}
$$
ここで、上記が全て$0$となるような$x_1,x_2,\lambda$を求める。$\displaystyle x_1 = \frac{1}{2 \lambda}$、$\displaystyle x_2 = \frac{1}{2 \lambda}$を$1 – (x_1^2 + x_2^2)=0$に代入し、$\displaystyle \lambda = \frac{1}{\sqrt{2}}$が求められる。
またこれを$\displaystyle x_1 = \frac{1}{2 \lambda}$、$\displaystyle x_2 = \frac{1}{2 \lambda}$に代入することで、$\displaystyle x_1 = \frac{\sqrt{2}}{2 \lambda}$、$\displaystyle x_2 = \frac{\sqrt{2}}{2 \lambda}$を得ることができ、これはi)の結果と一致する。
・解説
ラグランジュの未定乗数法は制約付き最適化問題をシンプルに取り扱うことができるので、様々な導出で用いられます。そのため一連の手順については必ず抑えておきたい内容です。
発展問題
ベクトルの正射影と分散の表記
・問題
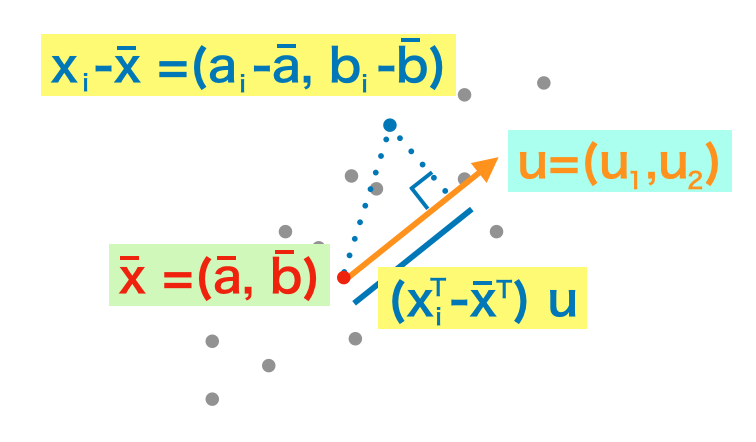
上図のようにサンプル群を考える。ここで、$i$番目のサンプルを2次元ベクトル$\displaystyle \mathbf{x}_i = \left(\begin{array}{c} a_i \\ b_i \end{array} \right)$、サンプルの平均ベクトルを$\displaystyle \mathbf{\bar{x}} = \left(\begin{array}{c} \bar{a} \\ \bar{b} \end{array} \right)$、単位ベクトルを$\displaystyle \mathbf{u} = \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right)$で定義する。
この時下記の問題に答えよ。
i) 下記の式は何を表すか答えよ。
$$
\begin{align}
(\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}) \mathbf{u} = (a_i-\bar{a})u_1 + (b_i-\bar{b})u_2
\end{align}
$$
ⅱ) 下記の式が成立することを確かめよ。
$$
\begin{align} \sum_{i=1}^{n}((\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}) \mathbf{u})^2 = \left(\begin{array}{cc} u_1 & u_2 \end{array} \right) \left(\begin{array}{rr} \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(b_i-\bar{b}) \\ \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(b_i-\bar{b}) \end{array} \right) \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right)
\end{align}
$$
ⅲ) ⅱ)の式は何を表すか答えよ。
・解答
i)
与えられた式は内積を計算しており、ベクトル$\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}$から$\mathbf{u}$への正射影を表している。また、$\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}$は$i$番目のサンプルの平均との差を表している。
ⅱ)
下記のように導出を行うことができる。
$$
\begin{align}
\sum_{i=1}^{n}((\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}) \mathbf{u})^2 &= \frac{1}{n}\sum_{i=1}^{n}((a_i-\bar{a})u_1 + (b_i-\bar{b})u_2)^2 \\
&= \frac{1}{n} \left(\begin{array}{ccc} (a_1-\bar{a})u_1 + (b_1-\bar{b})u_2 & … & (a_n-\bar{a})u_1 + (b_n-\bar{b})u_2 \end{array} \right) \left(\begin{array}{c} (a_1-\bar{a})u_1 + (b_1-\bar{b})u_2 \\ \vdots \\ (a_n-\bar{a})u_1 + (b_n-\bar{b})u_2 \end{array} \right) \\
&= \frac{1}{n} \left(\begin{array}{cc} u_1 & u_2 \end{array} \right) \left(\begin{array}{ccc} a_1-\bar{a} & … & a_n-\bar{a} \\ b_1-\bar{b} & … & b_n-\bar{b} \end{array} \right) \left(\begin{array}{cc} a_1-\bar{a} & b_1-\bar{b} \\ \vdots & \vdots \\ a_n-\bar{a} & b_n-\bar{b} \end{array} \right) \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right) \\
&= \frac{1}{n} \left(\begin{array}{cc} u_1 & u_2 \end{array} \right) \left(\begin{array}{cc} \displaystyle \sum_{i=1}^{n}(a_i-\bar{a})(a_i-\bar{a}) & \displaystyle \sum_{i=1}^{n}(a_i-\bar{a})(b_i-\bar{b}) \\ \displaystyle \sum_{i=1}^{n}(b_i-\bar{b})(a_i-\bar{a}) & \displaystyle \sum_{i=1}^{n}(b_i-\bar{b})(b_i-\bar{b}) \end{array} \right) \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right) \\
&= \left(\begin{array}{r} u_1 & u_2 \end{array} \right) \left(\begin{array}{rr} \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(b_i-\bar{b}) \\ \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(b_i-\bar{b}) \end{array} \right) \left(\begin{array}{c} u_1 \\ u_2 \end{array} \right)
\end{align}
$$
ⅲ)
ⅱ)の導出結果における$\displaystyle \left(\begin{array}{rr} \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(a_i-\bar{a})(b_i-\bar{b}) \\ \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(a_i-\bar{a}) & \displaystyle \frac{1}{n}\sum_{i=1}^{n}(b_i-\bar{b})(b_i-\bar{b}) \end{array} \right) $はサンプル$\mathbf{x}_i$の分散共分散行列を表している。
よって、ⅱ)の式はベクトル$\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}$から$\mathbf{u}$に正射影を行なった際の分散を$\mathbf{x}_i$の分散共分散行列を用いて表すことのできるということを意味している。
・解説
ⅱ)の変形は省略して記載されることが多いですが、この点を流すと導出の流れがわからなくなると思われるので、丁寧に確認しておくと良いと思います。ベクトルや行列に関する演算は省略されることが多いですが、なるべく要素を書き出すことで少しずつ理解する方が良いと思います。
主成分ベクトルと寄与率の導出
$2$次元のサンプル$\mathbf{x}_i$の分散共分散行列を$\Sigma$とする際に、$\mathbf{x}_i-\mathbf{\bar{x}}$の$2$次元ベクトル$\mathbf{u}$への正射影の分散は下記のように表すことができる。
$$
\begin{align} \sum_{i=1}^{n}((\mathbf{x}_i^{\mathrm{T}}-\mathbf{\bar{x}}^{\mathrm{T}}) \mathbf{u})^2 = \mathbf{u}^{\mathrm{T}} \Sigma \mathbf{u}
\end{align}
$$
ここで、$\mathbf{u}^{\mathrm{T}}\mathbf{u}=1$の制約下で下記の制約付き最適化問題を考える。
$$
\begin{align}
\mathrm{maximize} &: \quad f(\mathbf{u}) = \mathbf{u}^{\mathrm{T}} \mathbf{\Sigma} \mathbf{u} \\
\mathrm{constraint} &: \quad \mathbf{u}^{\mathrm{T}}\mathbf{u} = 1
\end{align}
$$
また、下記のようにベクトルを用いた偏微分の演算子$\nabla$を定義する。
$$
\begin{align}
\nabla = \frac{\partial}{\partial \mathbf{u}} = \left(\begin{array}{c} \displaystyle \frac{\partial}{\partial u_1} \\ \displaystyle \frac{\partial}{\partial u_2} \end{array} \right)
\end{align}
$$
このとき下記の問題に答えよ。
i) $\nabla \mathbf{u}^{\mathrm{T}} \mathbf{u}$を計算せよ。
ⅱ) $\Sigma$が対称行列であることに注意しつつ、$\nabla \mathbf{u}^{\mathrm{T}} \Sigma \mathbf{u}$を計算せよ。ただし、下記の結果を公式のように用いて良いものとする。
https://www.hello-statisticians.com/practice/stat_practice9.html#i-3
ⅲ) $g(\mathbf{u}) = \mathbf{u}^{\mathrm{T}} \Sigma \mathbf{u} + \lambda(1-\mathbf{u}^{\mathrm{T}}\mathbf{u})$とおくとき、$\nabla g(\mathbf{u}) = \mathbf{0}$の際に$\mathbf{\Sigma}\mathbf{u} = \lambda\mathbf{u}$が成立することを示せ。
iv) ⅲ)の$\mathbf{u}$はどのようなベクトルとなるか。
v) $\mathbf{\Sigma}\mathbf{u} = \lambda\mathbf{u}$に左から$\mathbf{u}^{\mathrm{T}}$をかけると$\lambda = \mathbf{u}^{\mathrm{T}}\mathbf{\Sigma}\mathbf{u}$が導出できる。この式を用いて第$1$主成分や寄与率を説明せよ。
・解答
i)
下記のように計算できる。
$$
\begin{align}
\nabla \mathbf{u}^{\mathrm{T}} \mathbf{u} = 2\mathbf{u}
\end{align}
$$
ⅱ)
$\Sigma$が対称行列であるので下記のように計算できる。
$$
\begin{align}
\nabla \mathbf{u}^{\mathrm{T}} \mathbf{\Sigma} \mathbf{u} = 2\mathbf{\Sigma}\mathbf{u}
\end{align}
$$
ⅲ)
i)、ⅱ)を元に、下記のように導出ができる。
$$
\begin{align}
\nabla g(\mathbf{u}) &= \mathbf{0} \\
2\mathbf{\Sigma}\mathbf{u} – 2\lambda\mathbf{u} &= 0 \\
\mathbf{\Sigma}\mathbf{u} &= \lambda\mathbf{u}
\end{align}
$$
iv)
$\mathbf{\Sigma}\mathbf{u} = \lambda\mathbf{u}$より、$\mathbf{u}$は$\mathbf{\Sigma}$の固有ベクトルとなる。
v)
$\lambda = \mathbf{u}^{\mathrm{T}}\mathbf{\Sigma}\mathbf{u}$の左辺は固有値、右辺は固有ベクトル$\mathbf{u}$に$\mathbf{x}_i-\mathbf{\bar{x}}$を射影した際の分散を意味する。
よって、固有値が正射影の分散に対応しており、最大固有値に対応する固有ベクトルが第$1$主成分となる。また、第$1$主成分の固有値を固有値の全体の和で割ることで寄与率を導出できる。たとえば第$1$主成分の寄与率が$95$%の場合、ほぼ第$1$主成分を考えるだけでサンプルの要約が可能となると考えることができる。
・解説
https://www.hello-statisticians.com/practice/stat_practice9.html#i-3
https://www.hello-statisticians.com/practice/stat_practice9.html#i-4
https://www.hello-statisticians.com/practice/stat_practice9.html#i-6
上記で確認したようなベクトルを用いた変形を理解することで、主成分分析の導出はシンプルに解くことができます。とはいえ個々の変形はそれぞれなかなか難しいので、何度か繰り返して慣れると良いと思います。
参考書籍
・「パターン認識と機械学習」

[…] ・問題フィッシャーの線形判別では郡内分散$V_W$と群間分散$V_B$を定義してその比の$displaystyle J(mathbf{w}) = frac{V_B}{V_W}$の最大化する$mathbf{w}$の導出を行う。最適化にあたっては$J(mathbf{w})$をベクトル$mathbf{w}$で微分するが、このときに「ベクトルを用いた微分」と「商の導関数」の理解が必須になる。「ベクトルを用いた微分」は「PCAの問題」で取り扱ったので、この問題では「商の導関数」の確認から$mathbf{w}$に関する最適化問題について取り扱う。 […]
[…] ↓演習問題https://www.hello-statisticians.com/practice/stat_practice9.html […]