離散型確率分布の数式まとめ（ベルヌーイ分布、二項分布、ポアソン分布、幾何分布 etc）

http://www.hello-statisticians.com/explain-terms-cat/prob_generating.html
上記では確率分布の様々な表記（確率密度関数、確率母関数など）について確認したが、当記事ではその表記に基づいて離散型確率分布のそれぞれの確率密度関数やモーメント母関数、期待値、分散などについて確認する。

離散型確率分布

ベルヌーイ分布

ベルヌーイ分布はベルヌーイ試行を元に定義する分布である。確率$p$で成功する試行を考えた際に、確率変数$X$を成功のとき$1$、失敗のとき$0$とするベルヌーイ試行に対し、確率変数Xの従う分布を成功確率$p$のベルヌーイ分布とし、$\mathrm{Bin}(1,p)$のように表す。ここで、$\mathrm{Bin}(1,p)$は二項分布の$\mathrm{Bin}(n,p)$において$n=1$とした場合であるとも考えることができる。

ベルヌーイ分布の確率関数は下記のように考えることができる。
$$
\large
\begin{align}
P(X=x) = p^x(1-p)^{1-x}
\end{align}
$$

次にベルヌーイ分布の期待値$E[X]$と分散$V[X]$について考える。
・期待値
$$
\large
\begin{align}
E[X] = 1 \times p + 0 \times (1-p) = p
\end{align}
$$

・分散
$$
\large
\begin{align}
V[X] &= E\left[X^2\right]-\left(E[X]\right)^2 \\
&= \left(1^2 \times p + 0^2 \times (1-p)\right) – p^2 \\
&= p-p^2 \\
&= p(1-p)
\end{align}
$$

また、確率母関数、モーメント母関数は下記のようになる。
・確率母関数
$$
\large
\begin{align}
G(t) &= E\left[t^X\right] = t^1 \times p + t^0 \times (1-p) \\
&= tp+(1-p) \\
&= tp + 1 – p
\end{align}
$$

・モーメント母関数
$$
\large
\begin{align}
m(t) &= E\left[e^{tX}\right] = e^{t \times 1} \times p + e^{t \times 0} \times (1-p) \\
&= e^t p + (1-p) \\
&= e^t p + 1 – p
\end{align}
$$

二項分布

二項分布はベルヌーイ分布と同様にベルヌーイ試行を元に定義する分布である。確率$p$で成功する試行を$n$回繰り返すと考えた際に、確率変数$X$を成功の回数すると、確率変数$X$の従う分布は試行回数$n$、成功確率$p$の二項分布となり、$\mathrm{Bin}(n,p)$のように表す。

二項分布の確率関数は下記のように考えることができる。
$$
\large
\begin{align}
P(X=k|n,p) = {}_n C_k p^{k}(1-p)^{n-k}
\end{align}
$$

次に二項分布の期待値$E[X]$と分散$V[X]$について考える。期待値や分散は独立なベルヌーイ分布の複数回試行であることを考慮することで求めやすい。$i$番目のベルヌーイ試行の確率変数を$X_i$とおくと、$X=X_1+X_2+…+X_n$とできるので期待値と分散は下記のように導出できる。
・期待値
$$
\large
\begin{align}
E[X] &= E[X_1+X_2+…X_n] \\
&= E[X_1]+E[X_2]+…+E[X_n] \\
&= np
\end{align}
$$

・分散
$$
\large
\begin{align}
V[X] &= V[X_1+X_2+…X_n] \\
&= V[X_1]+V[X_2]+…+V[X_n] \\
&= np(1-p)
\end{align}
$$

また、確率母関数、モーメント母関数は下記のようになる。
・確率母関数
$$
\large
\begin{align}
G(t) &= E\left[t^X\right] \\
&= \sum_{k=0}^{n} t^k \cdot {}_n C_k p^k (1-p)^{n-k} \\
&= \sum_{k=0}^{n} {}_n C_k (pt)^k (1-p)^{n-k} \\
&= (pt + 1 – p)^n
\end{align}
$$
計算にあたっては二項定理を利用した。

・モーメント母関数
$$
\large
\begin{align}
m(t) &= E\left[e^{tX}\right] \\
&= \sum_{k=0}^{n} e^{tk} \cdot {}_n C_k p^k (1-p)^{n-k} \\
&= \sum_{k=0}^{n} {}_n C_k (p e^t)^k (1-p)^{n-k} \\
&= (p e^t + 1 – p)^n
\end{align}
$$
確率母関数の計算と同様に導出にあたっては二項定理を利用した。また、モーメント母関数を活用することで二項分布の再生性を示すことができることも合わせて抑えておくとよい。
https://www.hello-statisticians.com/explain-terms-cat/probdist3.html

ポアソン分布

二項分布において$n$が大きい一方で$p$が小さい場合、双方の傾向がつりあって、それほど大きくないほどほどの$x$が現実には観察される。が、この確率を二項分布で表すと計算が煩雑になる。
たとえば$n=1000$、$p=0.002$の際に$x=3$となる確率は下記のようになる。
$$
\large
\begin{align}
{}_{1000} C_{3} (0.002)^{3}(0.998)^{997}
\end{align}
$$
上記のような計算を直接行うのはあまり望ましくない一方で、上記の期待値は$E[X]=np=2$であるから基本的には$x=0, 1, 2 ,3$くらいまでの確率は小さくないと考えることができる。

このような場合に$\lambda=np$を導入し、二項分布の極限を考えることで導出する分布がポアソン分布である。
$$
\large
\begin{align}
\lim_{n \to \infty} {}_n C_x p^x (1-x)^{n-x} = \frac{e^{-\lambda} \lambda^x}{x!}
\end{align}
$$

上記のように「ポアソンの小数の法則」に基づいて極限を考えることで、二項分布の式からポアソン分布の式を導出することができる。導出の詳細は下記の演習で取り扱った。

確率分布(probability distribution)｜基本演習で理解する統計学【5】

よってポアソン分布の確率関数は$\lambda=np$で定義される$\lambda$を用いて下記のように考えることができる。
$$
\large
\begin{align}
P(x|\lambda) = \frac{e^{-\lambda} \lambda^x}{x!}
\end{align}
$$

また、$\lambda=np=2$の時、$P(x=0|\lambda=2)$〜$P(x=3|\lambda=2)$はそれぞれ下記のような値となる。
$$
\large
\begin{align}
P(x=0|\lambda=2) &= \frac{e^{-2} \cdot 2^0}{0!} \\
&= e^{-2} \\
&= 0.1353095 \\
P(x=1|\lambda=2) &= \frac{e^{-2} \cdot 2^1}{1!} \\
&= 2 \cdot e^{-2} \\
&= 0.2706709 \\
P(x=2|\lambda=2) &= \frac{e^{-2} \cdot 2^2}{2!} \\
&= 2 \cdot e^{-2} \\
&= 0.2706709 \\
P(x=3|\lambda=2) &= \frac{e^{-2} \cdot 2^3}{3!} \\
&= \frac{4 \cdot e^{-2}}{3} \\
&= 0.180447
\end{align}
$$
このとき、上記の$4$つの$x$の値に関する和は$0.857…$となり、$\lambda=np=2$の場合は$x=0〜3$にほとんどの確率が集中することが見て取れる。

期待値$E[X]$や分散$V[X]$は二項分布の値に対して$\lambda = np$とした上で、$n \to \infty$、$p \to 0$の極限を考えることで導出できる。
・期待値
$$
\large
\begin{align}
E[X] &= np \\
&= \lambda
\end{align}
$$

・分散
$$
\large
\begin{align}
V[X] &= np(1-p) \\
&= \lambda(1-p) \\
& \to \lambda \quad (1-p \to 1)
\end{align}
$$

また、確率母関数、モーメント母関数は下記のようになる。
・確率母関数
$$
\large
\begin{align}
G(t) &= E\left[t^X\right] \\
&= \sum_{k=0}^{\infty} t^k \times \frac{\lambda^k e^{-\lambda}}{k!} \\
&= \sum_{k=0}^{\infty} \frac{(t \lambda)^k e^{-\lambda}}{k!} \\
&= e^{-\lambda} \sum_{k=0}^{\infty} \frac{(t \lambda)^k}{k!}
\end{align}
$$

ここで、$\displaystyle e^x$の$x=0$周辺でのマクローリン展開を考えると下記のようになる。
$$
\large
\begin{align}
e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!}
\end{align}
$$
上記より、$\displaystyle \sum_{k=0}^{\infty} \frac{(t \lambda)^k}{k!}$は$\displaystyle e^{t \lambda}$のようになる。よって、確率母関数$G(t)$は下記のように計算できる。
$$
\large
\begin{align}
G(t) &= e^{-\lambda} \sum_{k=0}^{\infty} \frac{(t \lambda)^k}{k!} \\
&= e^{-\lambda} \cdot e^{t \lambda} \\
&= e^{\lambda(t-1)}
\end{align}
$$

・モーメント母関数
$$
\large
\begin{align}
m(t) &= E\left[e^{tX}\right] \\
&= \sum_{k=0}^{\infty} e^{tk} \times \frac{\lambda^k e^{-\lambda}}{k!} \\
&= \sum_{k=0}^{\infty} \frac{(e^t \lambda)^k e^{-\lambda}}{k!} \\
&= e^{-\lambda} \sum_{k=0}^{\infty} \frac{(e^t \lambda)^k}{k!} \\
&= e^{-\lambda} \cdot e^{e^t \lambda} \\
&= e^{\lambda(e^t-1)}
\end{align}
$$
途中計算では確率母関数と同様に$e^x$のマクローリン展開を用いて変形を行った。また、モーメント母関数を活用することでポアソン分布の再生性を示すことができることも合わせて抑えておくとよい。
https://www.hello-statisticians.com/explain-terms-cat/probdist3.html

幾何分布

幾何分布はベルヌーイ試行を複数回行ったときに、最初に成功するまでの試行回数を$X$とした際の確率分布である。$X$の定義は「最初に成功するまでの失敗の回数」とするか「最初に成功するまでの試行の回数」とするかで$1$回異なるので注意しておきたい。準$1$級のワークブックでは失敗の数をカウントしているが、試行の数をカウントする方が一般的な印象を受けるのでここでは「成功するまでの試行」を考えるものとする。

まず、幾何関数の確率関数$P(X=x)$は下記のように考えることができる。
$$
\large
\begin{align}
P(X=x) = p(1-p)^{x-1}
\end{align}
$$
上記の解釈にあたっては、$x-1$回失敗したのちに成功する同時確率をそれぞれが独立な試行(ベルヌーイ試行)であることからそれぞれの起こる確率の積で表したと考えることができる。

次に幾何分布の期待値$E[X]$と分散$V[X]$について考える。
・期待値
$$
\large
\begin{align}
E[X] &= \sum_{x=1}^{\infty} xP(X=x) \\
&= \sum_{x=1}^{\infty} xp(1-p)^{x-1} \\
&= p \sum_{x=1}^{\infty} x(1-p)^{x-1} \\
&= p \left( 1 + 2(1-p)^{2-1} + 3(1-p)^{3-1} \cdots \right) \\
&= p \frac{1}{(1-(1-p))^2} \\
&= p \frac{1}{p^2} \\
&= \frac{1}{p}
\end{align}
$$
http://www.hello-statisticians.com/explain-terms-cat/maclaurin-seriese.html
の$(5)$式を用いて途中計算を行った。

・分散
期待値の計算で用いたマクローリン展開の両辺をさらに微分することで下記を得ることができる。
$$
\large
\begin{align}
\frac{1}{(1-x)^2} &= \sum_{n=1}^{\infty} nx^{n-1} = 1 + 2x^{2-1} + 3x^{3-1} \cdots \qquad 平均の計算で用いた \\
\left( \frac{1}{(1-x)^2} \right)’ &= \left( \sum_{n=1}^{\infty} nx^{n-1} \right)’ \\
\frac{2}{(1-x)^3} &= \sum_{n=2}^{\infty} n(n-1)x^{n-2} = 2x^{2-2} + 3 \cdot 2x^{3-2} + 4 \cdot 3x^{4-2} + 5 \cdot 4x^{5-2} + \cdots \qquad (A)
\end{align}
$$

途中計算で上記を用いる。
$$
\large
\begin{align}
V[X] &= E[X^2]-(E[X])^2 \\
&= E[X(X-1)]+E[X]-(E[X])^2
\end{align}
$$

分散$V[X]$に関して上記の数式が成立するが、$E[X]$については期待値で求めたので、$E[X(X-1)]$を求めることについて考える。
$$
\large
\begin{align}
E[X(X-1)] &= \sum_{x=2}^{\infty} x(x-1)P(X=x) \\
&= \sum_{x=2}^{\infty} x(x-1)p(1-p)^{x-1} \\
&= p(1-p) \sum_{x=2}^{\infty} x(x-1)(1-p)^{x-2} \\
&= p(1-p) \left( 2 + 3 \cdot 2(1-p)^{3-2} + 4 \cdot 3(1-p)^{4-2} + 5 \cdot 4(1-p)^{5-2} + \cdots \right) \\
&= p(1-p) \frac{2}{(1-(1-p))^3} \\
&= \frac{2p(1-p)}{p^3} \\
&= \frac{2(1-p)}{p^2}
\end{align}
$$
上記の途中計算で$(A)$で表したマクローリン展開の式を用いた。これにより、分散$V[X]$は下記のようになる。

$$
\large
\begin{align}
V[X] &= E[X^2]-(E[X])^2 \\
&= E[X(X-1)]+E[X]-(E[X])^2 \\
&= \frac{2(1-p)}{p^2} + \frac{1}{p} – \left( \frac{1}{p} \right)^2 \\
&= \frac{2(1-p)}{p^2} + \frac{p}{p^2} – \frac{1}{p} \\
&= \frac{2-2p+p-1}{p^2} \\
&= \frac{1-p}{p^2}
\end{align}
$$

・考察
幾何分布の平均・分散の計算ではマクローリン展開を逆に用いるが、確率変数の$X$とマクローリン展開の次数$n$の対応や$\displaystyle \sum$の始点の$n=1$や$x=2$の対応などがわかりにくい。よって、$\displaystyle \sum$の形式を$2 + 3 \cdot 2(1-p)^{3-2} + 4 \cdot 3(1-p)^{4-2} + 5 \cdot 4(1-p)^{5-2} + \cdots$のように和の形式に直した上でマクローリン展開を逆に用いてミスを減らすというのが実用的であるように思われる。

超幾何分布

$N$個のうち、$M$個が$A$で$N-M$個が$B$の袋から$n$個取り出すとき、取り出したAの個数を確率変数$X$で考えるとする。このとき、一度引いたものを袋に戻さないで次のものを引くことを非復元抽出と呼ぶが、非復元抽出で$n$個引くとき、$X$は超幾何分布に従う。

超幾何関数の確率関数$P(X=x)$は下記のように考えることができる。
$$
\large
\begin{align}
P(X=x|N,M,n) = \frac{{}_N C_x \cdot {}_{N-M} C_{n-x}}{{}_N C_n}
\end{align}
$$

下記で詳しく取り扱った。

超幾何分布(Hypergeometric distribution)の定義と期待値・分散

負の二項分布

負の二項分布$NB(r,p)$は確率$p$の事象$1$が$r$回起こるまでに$(1-p)$の事象$2$が$Y$回起こると考える場合の$Y$の分布である。$Y=y$回起こる確率を表す確率関数を$p(y)$とおくと、$p(y)$は下記のように表すことができる。

$$
\large
\begin{align}
p(y) &= {}_r H_{y} p^{r} (1-p)^{y}, \quad y=0,1,2, \cdots \\
{}_{r} H_{y} &= {}_{y+r-1} C_{y} = \frac{(y+r-1)(y+r-2) \cdots (r+1)r}{y!}
\end{align}
$$

上記の式の${}_{r} H_{y}$は「重複組み合わせ」であり、「$r$種類のものを重複して$y$個選ぶ際の選び方」のように一般的には定義される。ここで${}_{r} H_{y}={}_{y+r-1} C_{y}$であることは下記の図を元に理解すると良い。

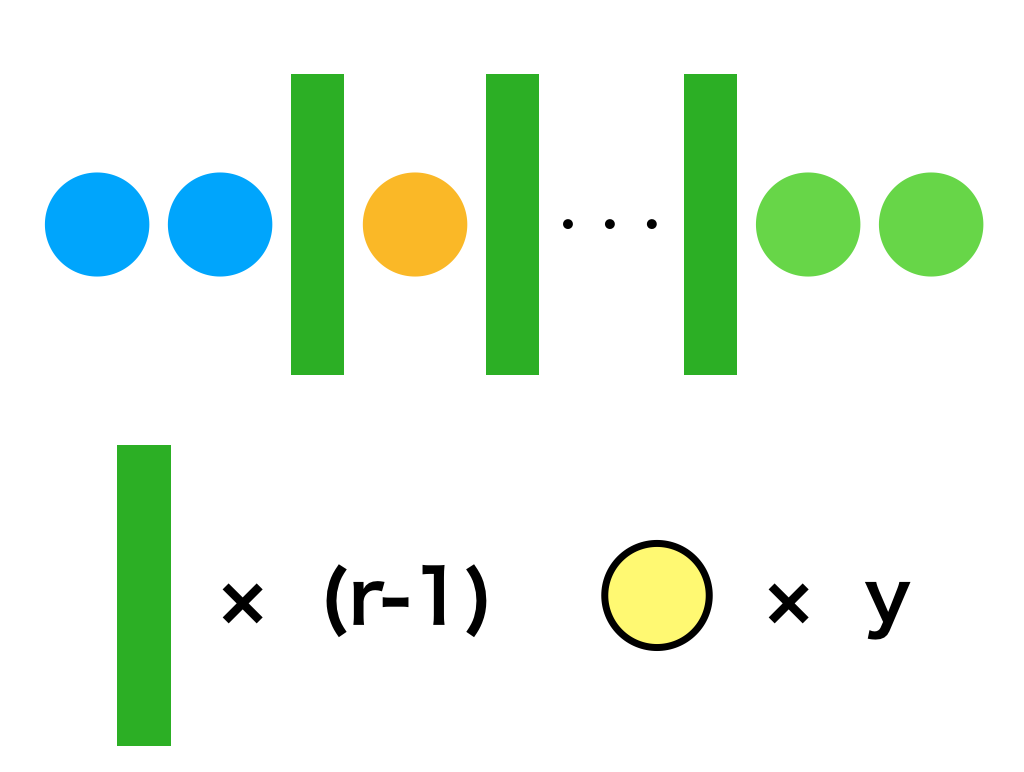
負の二項分布を考える場合は、「事象$1$の$1$回目が起こる直前に事象$2$が起こる、事象$1$の$2$回目が起こる直前に事象$2$が起こる、・・・、事象$1$の$r-1$回目が起こる直前に事象$2$が起こる」を$r$種類の重複組合せに対応すると解釈することで重複組合せを適用できる。

「負の二項分布」という名称は重複組合せ${}_{r} H_{y}$が『負の二項係数』を元に表せることに基づく。整数$a$と$0$以上の整数$b$に対し、二項係数の一般化を下記のように定める。
$$
\large
\begin{align}
\left(\begin{array}{c} a \\ b \end{array} \right) \equiv \frac{a(a-1) \cdots (a-b+1)}{b!}
\end{align}
$$

上記は${}_{a} C_{b}$と式自体は同様だが、$a$が$0$以下である場合も考えることに着目しておくと良い。${}_{a} C_{b}$の式を$a$が負の数も取り扱えるように拡張したと解釈すると良い。

ここで${}_{r} H_{y}$は$\displaystyle \left(\begin{array}{c} a \\ b \end{array} \right)$の表記を元に下記のように表すことができる。
$$
\large
\begin{align}
{}_r H_{y} &= {}_{y+r-1} C_{y} \\
&= \frac{(y+r-1)(y+r-2) \cdots (r+1)r}{y!} \\
&= \frac{r(r+1) \cdots (r+y-2)(r+y-1)}{y!} \\
&= (-1)^{y} \frac{(-r)(-r-1) \cdots (-r-y+2)(-r-y+1)}{y!} \\
&= (-1)^{y} \left(\begin{array}{c} -r \\ y \end{array} \right)
\end{align}
$$

上記のように重複組合せの${}_{r} H_{y}$に関して$\displaystyle {}_{r} H_{y} = (-1)^{y} \left(\begin{array}{c} -r \\ y \end{array} \right)$が成立することから「負の二項分布」という名称を抑えておくと良い。

また、$r=1$の負の二項分布$\mathrm{NB}(1,p)$は幾何分布$\mathrm{Geo}(p)$と対応することに基づいて負の二項分布の期待値と分散を導出することができる。$X_1, X_2, \cdots X_r \sim \mathrm{Geo}(p), \, \mathrm{i.i.d.,}$のとき、$E[X_i], V[X_i]$に関して下記が成立する。
$$
\large
\begin{align}
E[X_i] &= \frac{1}{p} \\
V[X_i] &= \frac{1-p}{p^2}
\end{align}
$$

よって確率変数$\displaystyle Y = \sum_{i=1}^{r} (X_i-1)$に関して下記が成立する。
$$
\large
\begin{align}
E[Y] &= E \left[ \sum_{i=1}^{r} (X_i-1) \right] = E \left[ -r + \sum_{i=1}^{r} X_i \right] \\
&= – r + \sum_{i=1}^{r} E[X_i] \\
&= -r+\frac{r}{p} = \frac{r(1-p)}{p} \\
V[Y] &= V \left[ \sum_{i=1}^{r} (X_i-1) \right] = V \left[ -r + \sum_{i=1}^{r} X_i \right] \\
&= 0 + \sum_{i=1}^{r} V[X_i] \\
&= \frac{r(1-p)}{p^2}
\end{align}
$$

上記が負の二項分布の期待値と分散に一致する。途中計算で用いた$E[X], V[X]$に関する公式の導出は下記で取り扱った。

抑えておきたい公式とその簡易的な導出に関して（期待値と分散・共分散）

多項分布

まとめ

当記事では離散型の確率分布について具体的に確認しました。二項分布、幾何分布はベルヌーイ分布の複数試行によって導出されることや、ポアソン分布は二項定理の事象が起こる確率が小さいかつ試行回数が多い際の二項分布の近似であることなどは抑えておくと良いと思います。

・基礎統計学Ⅰ 統計学入門(東京大学出版会)

・日本統計学会公式認定　統計検定準$1$級対応　統計学実践ワークブック

https://www.gakujutsu.co.jp/product/978-4-7806-0852-6/