整数の合同式に基づく線形合同法はシンプルでわかりやすい乱数生成方法である一方で、多次元分布を考える際に多次元疎結晶構造を生じるという課題があることに注意が必要です。当記事では線形合同法における多次元疎結晶構造をPythonなどを用いて図示を行いました。
・乱数生成の基本アルゴリズムまとめ
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html
「自然科学の統計学」の$11$章「乱数の性質」の解説などを参考に作成を行いました。
線形合同法における多次元疎結晶構造
線形合同法に基づく多次元の乱数の作成
$$
\large
\begin{align}
x_{n+1} = ax_{n} + c \quad (\mathrm{mod} \; M), \quad n \geq 1 \quad (1)
\end{align}
$$
上記の式で表される線形合同法を用いて多次元の乱数を作成することを考える。たとえば$M=16, a=5, c=1$の設定に対し、$x_0=0$を考えると下記のように乱数が生成される。
$$
\large
\begin{align}
x_1 &= 1, \, x_2 = 6, \, x_3 = 15, \, x_4 = 12, \, x_5 = 13, \\
x_6 &= 2, \, x_7 = 11, \, x_8 = 8, \, x_9 = 9, \, x_{10} = 14, \\
x_{11} &= 7, \, x_{12} = 4, \, x_{13} = 5, \, x_{14} = 10, \, x_{15} = 3, \\
x_{16} &= 0, \, x_{17} = 1, \, x_{18} = 6, \, x_{19} = 15, \, x_{20} = 12, \\
x_{21} &= 13, \, \cdots
\end{align}
$$
上記の周期は$M=16$に一致する。このように$M=2^n, a=4l+1, c=2l+1$に基づいて乱数を生成する場合、乱数の周期は$M=2^n$に一致するが、詳しくは下記で示した。
ここで$x_0=0, y_0=1$を元に$2$次元の一様乱数を生成することを考える。このとき、$y_0=x_1$であるので、乱数列${ x_n }$から隣接する$2$つの項を取り出し、$2$次元の乱数と見なしたと考えても同義である。
上記のように$2$つの乱数$(x_i,y_i=x_{i+1})$を生成し、$2$次元の一様分布と考えるというのは乱数生成における一般的な考え方である。一方で線形合同法でこのような方法で$2$次元の乱数を生成すると次節で取り扱う多次元疎結晶構造が生じるので注意が必要である。
多次元疎結晶構造
前節のように$M=16, a=5, c=1$の設定に基づいて初期値$x_0=0$から$(1)$式に基づいて乱数を生成した場合を考える。このとき、下記を実行することで$(x_i,x_{i+1})$を$2$次元平面状にプロットすることができる。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0., 1., 6., 15., 12., 13., 2., 11., 8., 9., 14., 7., 4., 5., 10., 3., 0.])
plt.scatter(x[:-1], x[1:])
plt.show()・実行結果
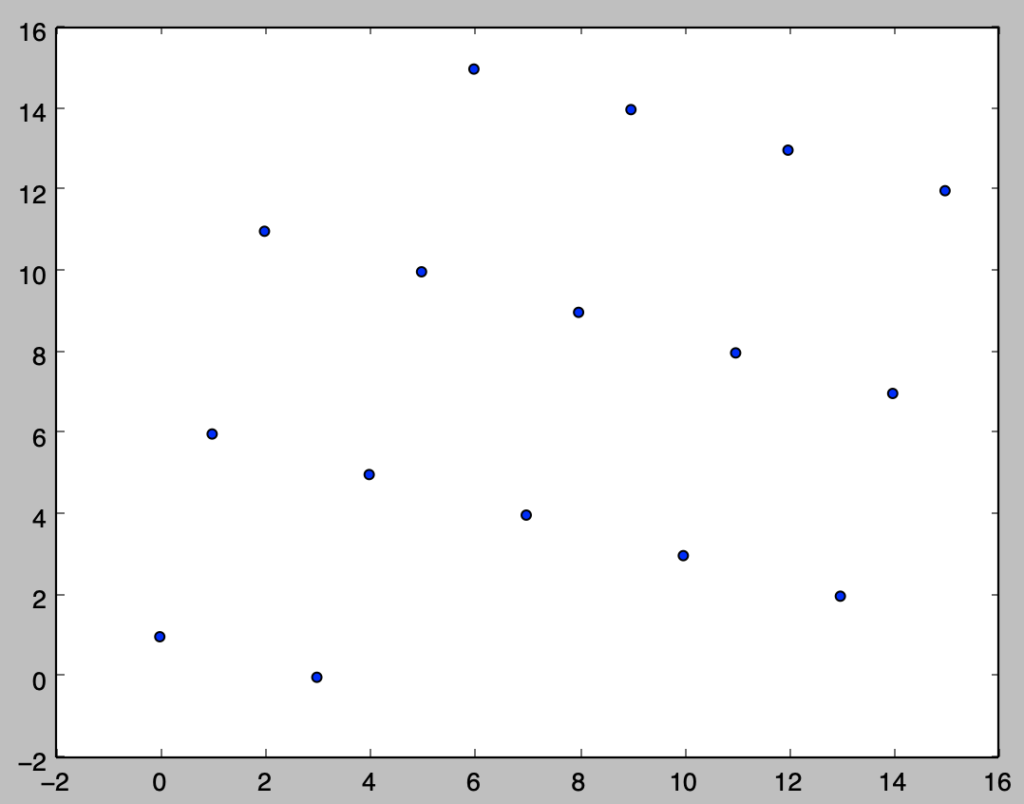
上図のように線形合同法を用いて$2$次元乱数を生成すると生成される乱数はいくつかの直線上に規則的に並ぶ。同様の事象が$k$次元の乱数を考えた際にも生じ、このことを多次元疎結晶構造という。多次元疎結晶構造であるかどうかを調べるにあたってはスペクトル検定などが用いられる。
多次元疎結晶構造やスペクトル検定に関しては「自然科学の統計学」の$11$章付節の「多次元疎結晶構造とスペクトル検定」を参照すると詳しい。

[…] 線形合同法(linear congruential method)における多次元疎結晶構造 […]
[…] ・問題「線形合同法・乗算型合同法」は多次元の一様分布の生成を行う際に適切な乱数が得られない「多次元疎結晶構造」を生じる。よって、実用的にはM系列という考え方に基づく一様乱数が用いられることが多く、現在多く使われるメルセンヌ・ツイスタ法もM系列に基づいた手法である。 […]