一様乱数を生成する手法は様々ですが、乱数の生成の際には乱数の周期に注意が必要です。当記事では一様乱数の生成にあたっての原始的かつシンプルな手法である線形合同法に基づいて乱数を生成する際に、最大周期を実現するにあたってのパラメータの設定とその導出について取りまとめを行いました。
・乱数生成の基本アルゴリズムまとめ
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html
Contents
前提の確認
線形合同法の概要
$$
\large
\begin{align}
x_{n+1} \equiv a x_{n} + c \quad (\mathrm{mod} \; M), \quad n \geq 1
\end{align}
$$
上記の式に基づいて一様乱数を生成する手法を線形合同法(LCG)という。詳しくは下記で取り扱った。
線形合同法による乱数列の最大周期
線形合同法では$\mathrm{mod} \; M$を考えるが$M$で割った余りは$0$から$M-1$の$M$通りである。よって線形合同法による乱数列の上限は$M$である。$M$はあくまで上限であり、たとえば$M=8,a=2,c=2$の場合は偶数しか生成されないので周期は$M$に一致しないことに注意が必要である。
逆に生成される乱数列が$M$に近い周期を持つ場合はすぐれた設定であると解釈できる。一方で$a=1,c=1$の場合は周期は$M$に一致するが、$1,2,3,4,5,\cdots$のように連番であり、良い乱数列であると言えない。このように$M,a,c$の設定は乱数生成の質に関わる重要な作業であると理解しておくと良い。
最大周期をもたらす設定とその証明
$M=2^n, \, a=4l+1, \, c=2m+1$
周期が$2^{n}$であることの証明
整数$l,m,n$を用いて$M=2^n, \, a=4l+1, \, c=2m+1$のように設定される場合に、生成される乱数列の周期は最大周期$M=2^n$に一致する。以下このことを数学的帰納法を用いて証明する。
i) $n=1,M=2^1=2$の場合
線形合同法における漸化式は下記のように表される。
$$
\large
\begin{align}
a x_{i} + c &= (4l+1) x_i + 2m + 1 \\
&= 2(2l x_i + m) + x_n + 1 \\
& \equiv x_i + 1 \equiv x_{i+1} \quad (\mathrm{mod} \; M)
\end{align}
$$
上記より$\mathrm{mod} \; M$で$x_{i+1} \equiv x_i + 1$が成立することより、$2$で割った余りに$0,1$が交互に出現すると考えることができる。よって$n=1$のとき$M=2^n, \, a=4l+1, \, c=2m+1$の設定における最大周期は$M$である。
ⅱ) $n=k,M=2^k$で成立する場合に$n=k+1,M=2^{k+1}$で成立するか
$2$で割った余りが$0,1$で循環する場合、$4$で割った余りが$0,0,0,\cdots$や$1,1,1,\cdots$にはなり得ない。同様に、「①$n=k,M=2^k$で成立する場合は、$\mathrm{mod} \; 2^{k+1}$を考えても$M=2^k$の周期よりも小さくなることはない」。
次に、「②$n=k,M=2^k$で成立する場合は、$x_i=j, \, 0 \leq j \leq 2^{k}-1$と$x_i=2^{k}+j$に対する$\mathrm{mod} \; 2^{k+1}$での$x_{j+1}$が異なる」ことを示す。
・$x_i=j$のとき
$$
\large
\begin{align}
a x_{i} + c = (4l+1)j + 2m + 1
\end{align}
$$
・$x_i=2^{k}+j$のとき
$$
\large
\begin{align}
a x_{i} + c &= (4l+1)(2^{k}+j) + 2m + 1 \\
&= 2^{k+2} + 2^{k} + (4l+1)j + 2m + 1 \\
& \equiv 2^{k} + (4l+1)j + 2m + 1 \quad (\mathrm{mod} \; 2^{k+1})
\end{align}
$$
$2^{k} + (4l+1)j + 2m + 1-((4l+1)j + 2m + 1)=2^{k}$であることから、$\mathrm{mod} \; 2^{k+1}$では「$x_i=j$と$x_i=2^{k}+j$に対する$x_{j+1}$が異なる」ことが示される。
①と②が成立するので「$n=k,M=2^k$で成立するとき$M=2^{k+1}$を考えると周期$2^k$の乱数列が並ぶか周期$2^{k+1}$の乱数列が並ぶかのどちらかである」と考えることができ、下記のように図示できる。
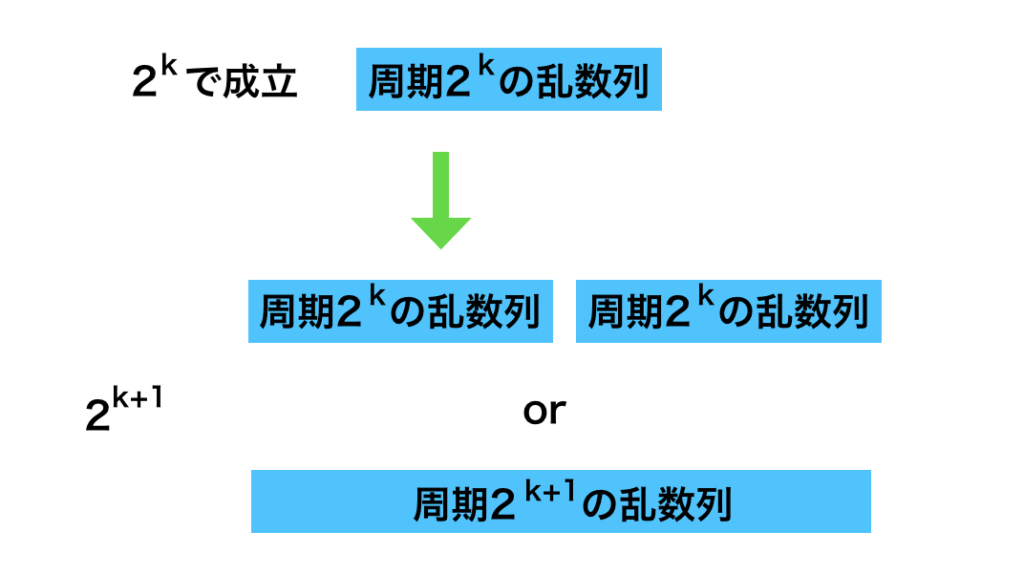
上図が成立することから、「③$x_i=0$のとき$x_{i+2^{2^{k}}} \neq x_i$」を示せば乱数列の周期が$2^{k+1}$であることを示すことができる。$x_i=0$のとき$x_{i+2^{2^{k}}}$は下記のように表せる。
$$
\large
\begin{align}
x_{i+2^{2^{k}}} – \frac{2m+1}{4l} & \equiv (4l+1)^{2^{k}} \left( x_0 – \frac{2m+1}{4l} \right) \\
&= – \frac{2m+1}{4l}(4l+1)^{2^{k}} \\
&= – \frac{2m+1}{4l} \sum_{j=0}^{2^{k}} {}_{2^{k}} C_{j} (4l)^{j} \\
x_{i+2^{2^{k}}} &= \frac{2m+1}{4l} – \frac{2m+1}{4l} \sum_{j=0}^{2^{k}} {}_{2^{k}} C_{j} (4l)^{j} \\
&= – \frac{2m+1}{4l} \sum_{j=1}^{2^{k}} {}_{2^{k}} C_{j} (4l)^{j} \\
& \equiv – \frac{2m+1}{4l} \times {}_{2^{k}} C_{1} (4l)^{1} \\
& \equiv -2^{k}(2m+1) \\
& \equiv 2^{k}
\end{align}
$$
よって③が成立する。①、②、③より「$n=k,M=2^k$周期が$2^{k}$が成立する場合に$n=k+1,M=2^{k+1}$で周期が$2^{k+1}$」が成立する。i)、ⅱ)より任意の自然数$n$に関して「$M=2^n, \, a=4l+1, \, c=2m+1$」の設定の周期が$2^n$であることが示される。
$M=2^n, \, a=4l+1, \, c=2m+1$の設定の注意点
前項の導出では数学的帰納法を用いたが、i)で確認したように$x_i$を$2$で割った余りが$0,1,0,1,0,\cdots$のように繰り返す。よってこの設定に基づいて生成される乱数は偶数と奇数が交互に入れ替わる乱数となる。
乱数の生成にあたっては可能な限り規則性のない数の並びを生成する必要があることから、「偶奇が必ず入れ替わる」のはそれほど良い乱数列ではないことに注意が必要である。
参考
・自然科学の統計学 Ch$.11$:乱数の性質

[…] 一様乱数の生成に用いる線形合同法(LCG)の最大周期の法則の証明 […]