あつまれ統計の森

Hello Statisticians!

メルセンヌ・ツイスタ(Mersenne Twister)法まとめ

投稿日: 投稿者: lib-arts

当記事では乱数生成にあたって近年用いられることの多いメルセンヌ・ツイスタ(Mersenne Twister)法の仕組みなどについて取りまとめを行いました。メルセンヌ・ツイスタ法はGFSRやTwisted GFSRが元になるので、合わせて取り扱いました。

・乱数生成まとめ
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html

原理の理解

M系列

$$
\large
\begin{align}
a_{n} = a_{n-q}+a_{n-p} \quad (\mathrm{mod} \; 2, \; q<p)
\end{align}
$$

$M$系列では上記のような漸化式に基づき乱数列を生成し、連続する$a_n$をビットと見なし乱数生成を行う。数列${a_n}$から連続する$2$つの数字を$2$ビットと見なし乱数を生成する方法は下記で詳しく取り扱った。

乱数生成の基本アルゴリズムまとめ（線形合同法、M系列、中心極限定理の応用 etc）

M系列に関しては「自然科学の統計学」の$11$章が詳しいので合わせて参照すると良い。

自然科学の統計学 (基礎統計学)

自然科学の統計学 (基礎統計学)

3,190円(04/25 14:47時点)
Amazon

LFSR法

LFSR($1965$)はLinear Feedbacked Shift Registerの略であり、Tauswortheにより発表されたことからTausworthe法ともいわれる。要出典・要確認だが、基本的には前項のM系列と同様であると考えて良いと思われる。

GFSR

Lewis-PayneによるGFSR($1973$)はLFSRの数列をベクトル列に変えた手法である。GFSRはGeneral Feedbacked Shift Registerの略であり、LFSR法を発展させた手法であることが名称からも読み取れる。
$$
\large
\begin{align}
\vec{x}_{n+p} \equiv \vec{x}_{n+q} + \vec{x}_{n} \quad (\mathrm{mod} \; 2, \; q<p)
\end{align}
$$

GFSRのベクトル漸化式は上記のように表されるが、式だけではわかりにくいので以下、具体的な数字に基づいて計算を行う。GFSR論文のFig.$4$を参考に、$p=5, q=2$のとき$\vec{x}_{0}^{\mathrm{T}}$〜$\vec{x}_{4}^{\mathrm{T}}$を下記のように定める。
$$
\large
\begin{align}
\vec{x}_{0}^{\mathrm{T}} &= \left( \begin{array}{c} 1 \\ 1 \\ 0 \\ 1 \\ 0 \end{array} \right), \quad \vec{x}_{1}^{\mathrm{T}} = \left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{array} \right), \quad \vec{x}_{2}^{\mathrm{T}} = \left( \begin{array}{c} 1 \\ 1 \\ 0 \\ 1 \\ 1 \end{array} \right) \\
\vec{x}_{3}^{\mathrm{T}} &= \left( \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ 0 \end{array} \right), \quad \vec{x}_{4}^{\mathrm{T}} = \left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 1 \\ 1 \end{array} \right)
\end{align}
$$

このとき$\vec{x}_{5}^{\mathrm{T}}$〜$\vec{x}_{7}^{\mathrm{T}}$はそれぞれ下記のように計算できる。

・$\vec{x}_{5}^{\mathrm{T}}$
$$
\large
\begin{align}
\vec{x}_{0+5} &= \vec{x}_{0+2} + \vec{x}_{0} \\
&= \left( \begin{array}{c} 1 \\ 1 \\ 0 \\ 1 \\ 1 \end{array} \right) + \left( \begin{array}{c} 1 \\ 1 \\ 0 \\ 1 \\ 0 \end{array} \right) \\
&= \left( \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{array} \right) \quad (\mathrm{mod} \; 2)
\end{align}
$$

・$\vec{x}_{6}^{\mathrm{T}}$
$$
\large
\begin{align}
\vec{x}_{1+5} &= \vec{x}_{1+2} + \vec{x}_{1} \\
&= \left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{array} \right) + \left( \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ 0 \end{array} \right) \\
&= \left( \begin{array}{c} 0 \\ 1 \\ 1 \\ 0 \\ 1 \end{array} \right) \quad (\mathrm{mod} \; 2)
\end{align}
$$

・$\vec{x}_{7}^{\mathrm{T}}$
$$
\large
\begin{align}
\vec{x}_{2+5} &= \vec{x}_{2+2} + \vec{x}_{2} \\
&= \left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 1 \\ 1 \end{array} \right) + \left( \begin{array}{c} 1 \\ 1 \\ 0 \\ 1 \\ 1 \end{array} \right) \\
&= \left( \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{array} \right) \quad (\mathrm{mod} \; 2)
\end{align}
$$

ここまでの結果はGFSR論文のFig.$4$に一致する。

GFSR論文 Fig.$4$

Twisted GFSR

$$
\large
\begin{align}
\vec{x}_{n+p} &= \vec{x}_{n+q} + \vec{x}_{n} A \quad (\mathrm{mod} \; 2, \; q<p) \\
A &= \left( \begin{array}{ccccc} & 1 & & \cdots & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \\ a_0 & a_1 & \cdots & \cdots & a_{w-1} \end{array} \right)
\end{align}
$$

Twisted GFSR法ではGFSR法の漸化式の一部をフロベニウスの同伴行列(companion matrix)の$A$で攪拌させることで周期の上限が$2^{p}-1$であるGFSR法に対し、周期の上限が$2^{wp}-1$を実現できる。詳しい処理は次節でプログラムを元に確認を行った。

上記で定めたフロベニウスの同伴行列(companion matrix)の$A$に関しては、下記で詳しく取り扱った。

フロベニウスの同伴行列(companion matrix)の定義と応用

メルセンヌ・ツイスタ法

$$
\large
\begin{align}
\vec{x}_{n+p} = \vec{x}_{n+q} + \vec{x}_{n+1} B + \vec{x}_{n} C \quad (\mathrm{mod} \; 2, \; q<p)
\end{align}
$$

メルセンヌ・ツイスタ法は上記の漸化式で表される。$B, C$に関しては「$\vec{x}_{n+1} B + \vec{x}_{n} C$」が「$\vec{x}_{n}$の上位$w-r$ビットと$\vec{x}_{n+1}$の下位$r$ビットで構成したビットを$\vec{x}_{n}’$とおくとき、$\vec{x}_{n}’=(\vec{x}_{n+1} B + \vec{x}_{n} C)A$が成立するような行列」と理解すると良い。このように生成した乱数は$2^{wp-r}-1$の最大周期を実現できる。

ここで$2^{wp-r}-1=2^{624 \times 32 – 31}-1 = 2^{19937}-1$のようにメルセンヌ素数を用いることができ、このことにより超長周期を実現することができる。メルセンヌ素数に関しては下記で詳しく取り扱った。

メルセンヌ数(Mersenne Number)と完全数(Perfect Number)

プログラム

Twisted GFSR

Cのプログラムの確認

/* A C-program for TT800 : July 8th 1996 Version */
/* by M. Matsumoto, email: matumoto@math.keio.ac.jp */
/* genrand() generate one pseudorandom number with double precision */ /* which is uniformly distributed on [0,1]-interval */
/* for each call. One may choose any initial 25 seeds */
/* except all zeros. */
/* See: ACM Transactions on Modelling and Computer Simulation, */
/* Vol. 4, No. 3, 1994, pages 254-266. */
#include <stdio.h>
#define N 25
#define M 7

double
genrand()
{
    unsigned long y;
    static int k = 0;
    static unsigned long x[N]={ /* initial 25 seeds, change as you wish */
        0x95f24dab, 0x0b685215, 0xe76ccae7, 0xaf3ec239, 0x715fad23,
        0x24a590ad, 0x69e4b5ef, 0xbf456141, 0x96bc1b7b, 0xa7bdf825,
        0xc1de75b7, 0x8858a9c9, 0x2da87693, 0xb657f9dd, 0xffdc8a9f,
        0x8121da71, 0x8b823ecb, 0x885d05f5, 0x4e20cd47, 0x5a9ad5d9,
        0x512c0c03, 0xea857ccd, 0x4cc1d30f, 0x8891a8a1, 0xa6b7aadb
    };
    static unsigned long mag01[2]={
        0x0, 0x8ebfd028 /* this is magic vector ‘a’, don’t change */
    };
    if (k==N) { /* generate N words at one time */
      int kk;
      for (kk=0;kk<N-M;kk++) {
        x[kk] = x[kk+M] ^ (x[kk] >> 1) ^ mag01[x[kk] % 2];
      }
      for (; kk<N;kk++) {
        x[kk] = x[kk+(M-N)] ^ (x[kk] >> 1) ^ mag01[x[kk] % 2];
      }
k=0; }
    y = x[k];
    y ^= (y << 7) & 0x2b5b2500; /* s and b, magic vectors */
    y ^= (y << 15) & 0xdb8b0000; /* t and c, magic vectors */
    y &= 0xffffffff; /* you may delete this line if word size = 32 */
    y ^= (y >> 16); /* added to the 1994 version */
    k++;
    return( (double) y / (unsigned long) 0xffffffff);
}
/* this main() output first 50 generated numbers */
main()
{ int j;
  for (j=0; j<50; j++) {
    printf("%5f ", genrand());
    if (j%8==7) printf("\n");
}
  printf("\n");
}

講義資料：有限体の擬似乱数への応用

上記のプログラムのx[N]は乱数の初期シード、mag01[2]は同伴行列$A$の$a_0, \cdots a_{w-1}$にそれぞれ対応する。mag01[2]に関して”this is magic vector ‘a’, don’t change”とあるので、同伴行列は乱数生成の際は固定であることが確認できる。

また、0x95f24dabの0xは$16$進数であることを意味しており、$0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f$の$16$個の文字が用いられる。

ここまで確認した内容により、同伴行列の構成と乱数の初期値が得られるので、次項では前節で確認した漸化式と当項で確認した同伴行列や乱数の初期値を元にPythonで乱数生成を行う。

Pythonでの再現

Twisted GFSR法はPythonを用いて下記のように再現することができる。

import numpy as np
import matplotlib.pyplot as plt

init_x = [bin(0x95f24dab), bin(0x0b685215), bin(0xe76ccae7), bin(0xaf3ec239), bin(0x715fad23), bin(0x24a590ad), bin(0x69e4b5ef), bin(0xbf456141), bin(0x96bc1b7b), bin(0xa7bdf825), bin(0xc1de75b7), bin(0x8858a9c9), bin(0x2da87693), bin(0xb657f9dd), bin(0xffdc8a9f), bin(0x8121da71), bin(0x8b823ecb), bin(0x885d05f5), bin(0x4e20cd47), bin(0x5a9ad5d9), bin(0x512c0c03), bin(0xea857ccd), bin(0x4cc1d30f), bin(0x8891a8a1), bin(0xa6b7aadb)]

x = np.zeros([100000, 2**5])
for i in range(len(init_x)):
    init_num = 2**5-len(list(init_x[i][2:]))
    x[i,init_num:] = np.array(list(init_x[i][2:]))

a = bin(0x8ebfd028)
init_num_a = 2**5-len(list(a[2:]))
A = np.zeros([2**5, 2**5])
for i in range(A.shape[0]-1):
    A[i,i+1] = 1.

A[-1,init_num_a:] = np.array(list(a[2:]))

for i in range(x.shape[0]-25):
    x[i+25,:] = (x[i+7,:] + np.dot(x[i,:],A))%2

numbers = np.zeros(x.shape[0])
for i in range(x.shape[0]):
    for j in range(x.shape[1]):
        numbers[i] += x[i,j]*2**(2**5-1-j)

plt.hist(numbers%100, bins=100)
plt.show()

・実行結果

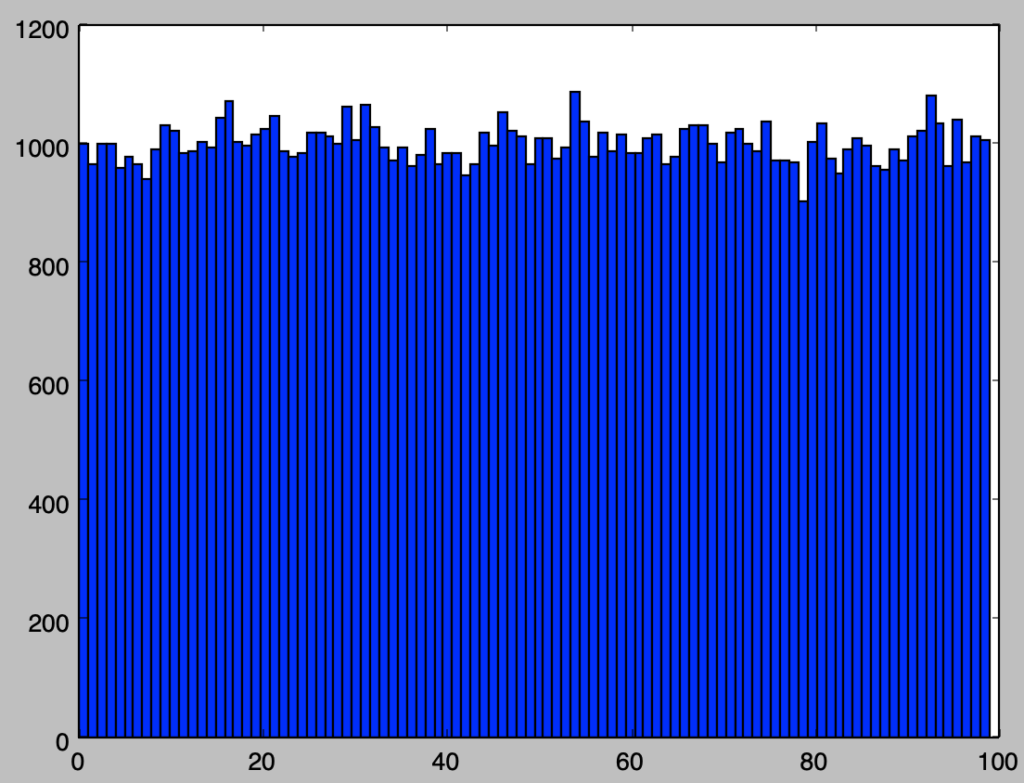
妥当な一様乱数が得られたかどうかを大まかに確認するにあたって、上記では得られた乱数を$100$で割った余りに関してヒストグラムの作成を行った。

メルセンヌ・ツイスタ法

Cのプログラムの確認

下記でプログラムが確認できる。
http://www.math.sci.hiroshima-u.ac.jp/m-mat/MT/MT2002/CODES/mt19937ar.c

Pythonでの再現

メルセンヌツイスタ法はPythonを用いて下記のように再現することができる。

import numpy as np
import matplotlib.pyplot as plt

N = 624
M = 397
a = 0x9908b0df

numbers = np.zeros(1000000)

numbers[0] = 19650218 & 0xffffffff
for i in range(1,N):
    numbers[i] = (1566083941 * (int(numbers[i-1]) ^ (int(numbers[i-1]) >> 30)) + i) & 0xffffffff

for i in range(numbers.shape[0]-N):
    num = (int(numbers[i+1]) & 0x7fffffff) + (int(numbers[i]) & 0x80000000)
    if num & 0x1 == 0:
        numbers[i+N] = int(numbers[i+M]) ^ (num >> 1)
    else:
        numbers[i+N] = int(numbers[i+M]) ^ ((num >> 1) ^ a)

plt.hist(numbers%500, bins=500)
plt.show()

・実行結果

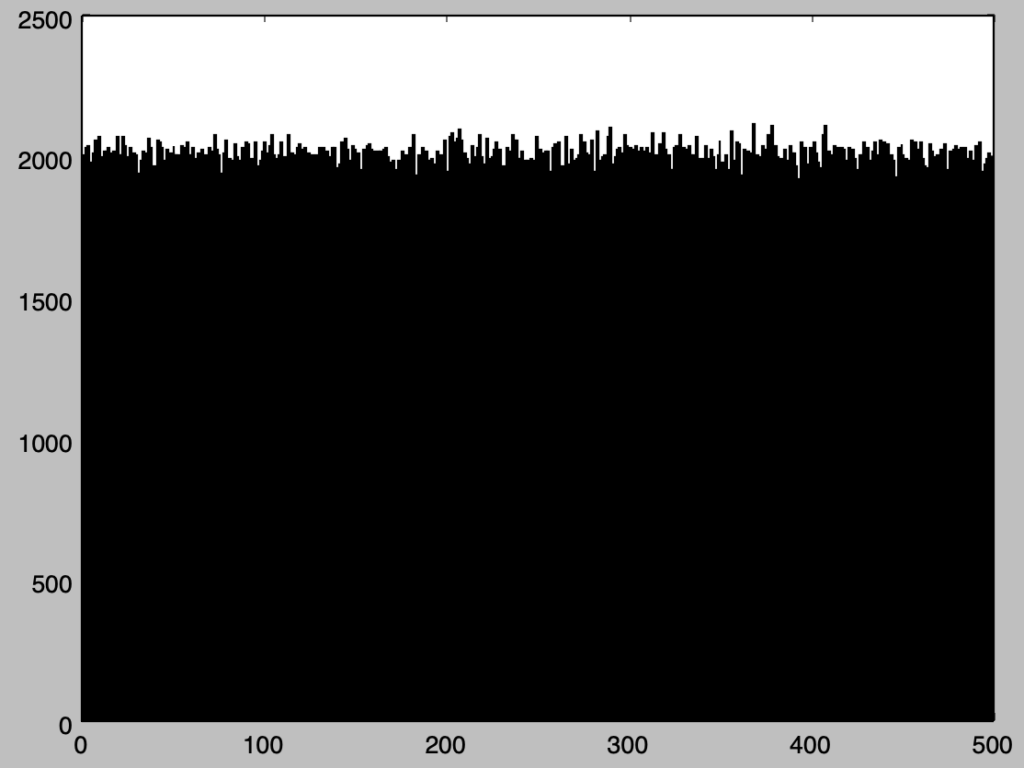
初期値の作成が元コードには準拠していないが、乱数生成部分に関しては同様な処理を再現した。実行結果では一様乱数が得られており、概ね妥当な結果が得られたと判断できる。途中の処理で用いたビット演算は下記で詳しく取りまとめた。

Pythonを用いた2進数(binary number)などの表記とビット演算

参考

・資料：第$50$回市村学術賞記念 先端技術講演会
・講義資料：有限体の擬似乱数への応用
・Wikipedia：メルセンヌ・ツイスタ
・Wikipedia：M系列
・Wikipedia：線形帰還シフトレジスタ
・論文：GFSR
・論文：Twisted GFSR
・論文：メルセンヌ・ツイスタ

「メルセンヌ・ツイスタ(Mersenne Twister)法まとめ」への5件のフィードバック

  4. […] ・問題「線形合同法・乗算型合同法」は多次元の一様分布の生成を行う際に適切な乱数が得られない「多次元疎結晶構造」を生じる。よって、実用的にはM系列という考え方に基づく一様乱数が用いられることが多く、現在多く使われるメルセンヌ・ツイスタ法もM系列に基づいた手法である。 […]

コメントは受け付けていません。