当記事では離散型確率分布に基づく乱数生成の手法である別名(alias)法に関して手順とPythonプログラムに関して取りまとめを行いました。途中で用いる$2$点分布の取り扱いなど、少々手順が複雑なのでなるべく直感的に理解できるような構成になるように取りまとめを行いました。
一様乱数の生成などの他の乱数生成の手法に関しては下記で取りまとめを行いましたので、こちらも合わせてご確認ください。
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html
「自然科学の統計学」の$11.4.2$節を参考に作成を行いました。
Contents
別名法の手順
別名法の概要
$K=5$の確率変数に対し、$p(X=1)=0.12, p(X=2)=0.24, p(X=3)=0.38, p(X=4)=0.16, p(X=5)=0.10$のような離散型確率分布を考える。この例は結果の確認が行いやすいように「自然科学の統計学」と同様のものを用いた。下記ではこの確率分布の確率関数に$K$をかけてグラフ化を行なった。
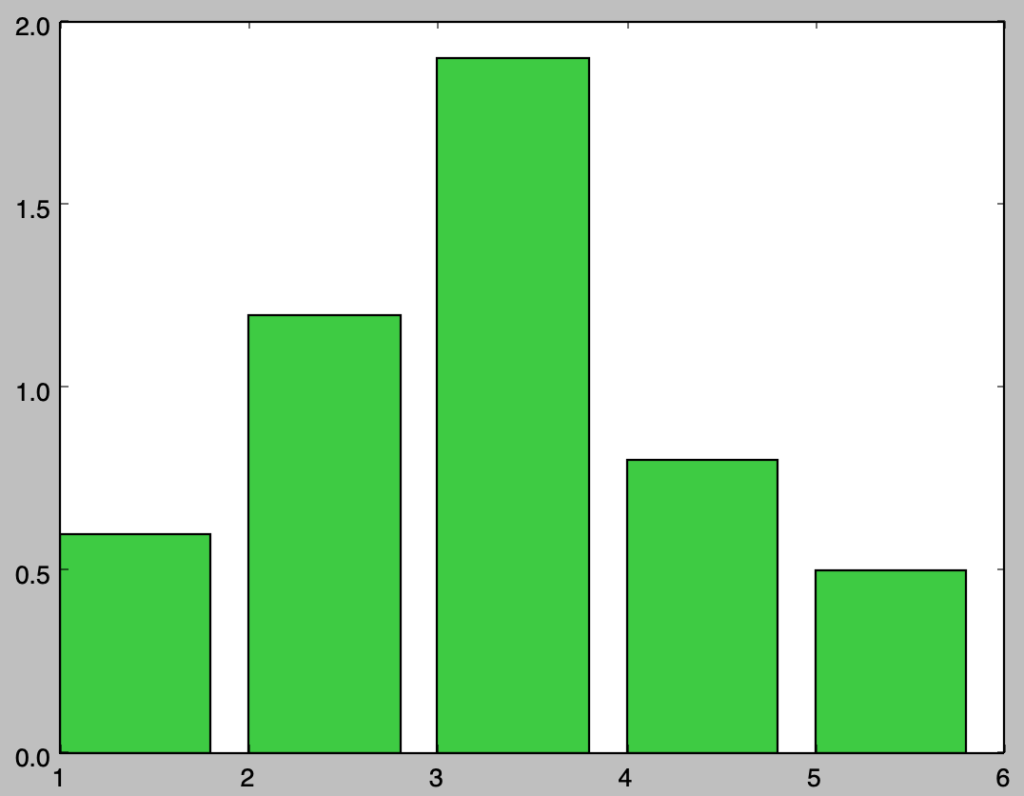
上記は離散型確率分布の確率関数に確率変数の数をかけたものであり、確率分布が一様であれば値が$1$に一致するように調整を行なったと考えればよい。ここで基礎的な乱数生成の手法は一様分布で得られることから、逆に「一様分布から得たサンプルを離散型確率分布に従うように補正する」手法について考える。この手法は、グラフの$1$以上を削り$1$以下に配分する一方でどこの値から削ったものかを把握しておくことで実現できる。
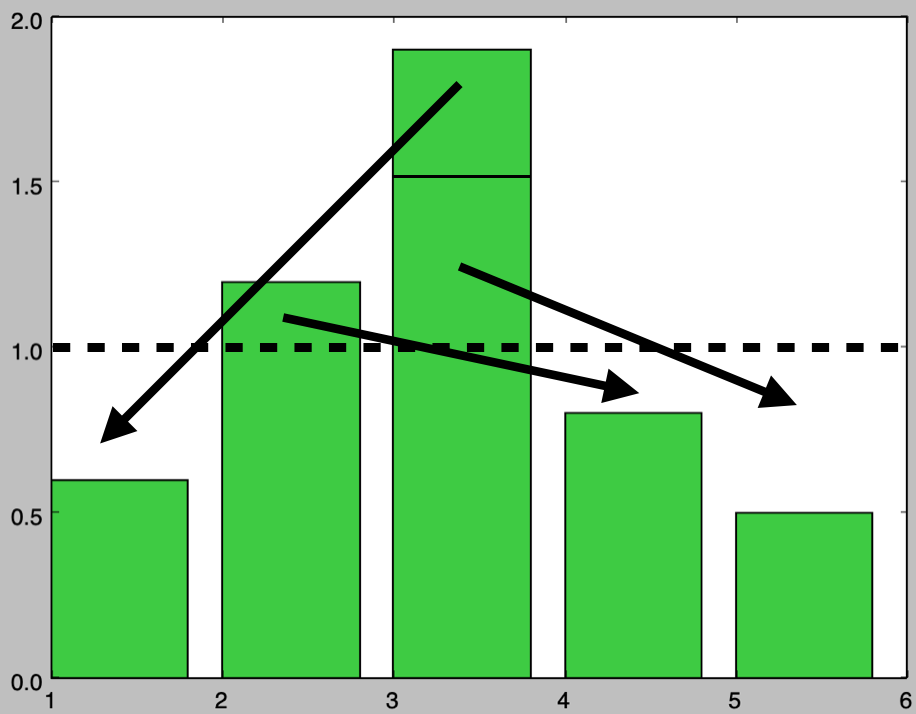
上図のように分布を配分しておくと、乱数生成の際は一様分布から逆に辿ることで確率の大きな確率変数が生成される。この詳しい手順に関して以下、数式とPythonプログラムを元に取りまとめる。
離散型確率分布の一様分布化
前項で取り扱った概要を実現するにあたっては、「①離散型確率分布の一様分布化」と「②乱数の生成」の二つのステップが必要になる。当項では「①離散型確率分布の一様分布化」の手順に関してまとめる。
諸々を数式を用いて表すにあたって、確率変数を$X$、確率変数のインデックスを整数$k, 1 \leq k \leq K$、$X=k$における確率関数を$p_{k}=P(X=k)$で表す。また、一様分布に基づいて乱数$k$を生成したのちに対応する確率変数を採択する確率を$v_{k}$、採択されない場合に採択する確率変数を$a_{k}$で定める。このとき、$v_{k}$と$a_{k}$は以下の手順に沿うことでそれぞれ自動的に計算を行うことができる。
$[1].$ $v_k \leftarrow Kp_{k} \quad 1 \leq k \leq K$
$[2].$ $v_{k} \geq 1$の$k$の集合を$G$、$v_{k} < 1$の$k$の集合を$S$とおく。
$[3].$ $S$が空集合でない限り以下の$[3.1]$〜$[3.4]$を繰り返し実行する。
$[3.1]$ $S, G$から$1$つずつ任意の要素を選び、$k,l$とおく。
$[3.2]$ $a_{k} \leftarrow l, v_{l} \leftarrow v_{l}-(1-v_{k})$
$[3.3]$ $S$から$k$を取り除く。
$[3.4]$ $v_{l} < 1$なら$l$を$G$から$S$に移す。
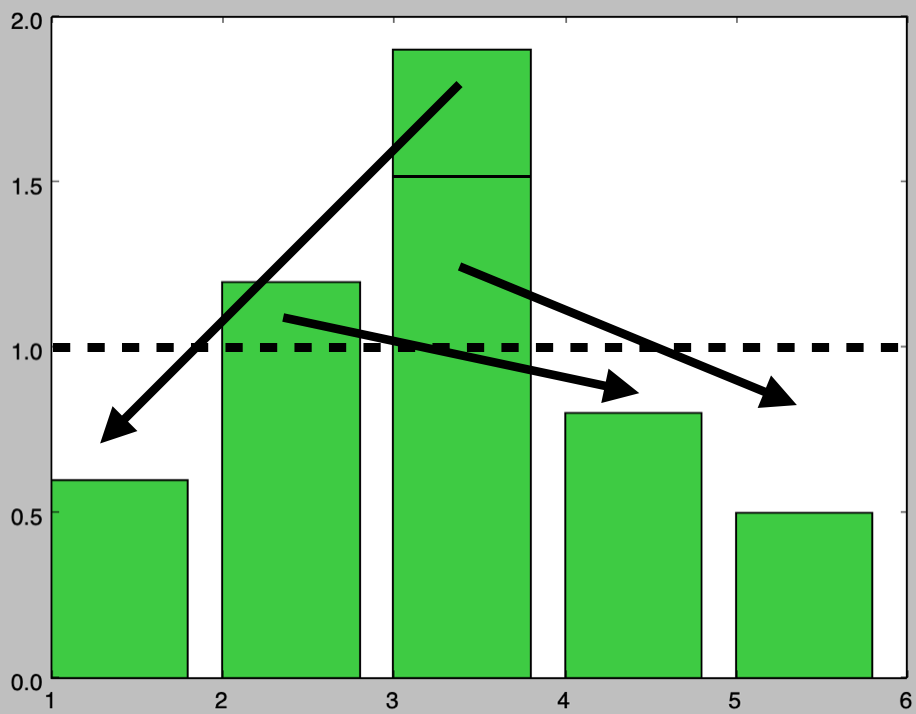
基本的には前項でも取り扱った上図に基づいた処理であるが、$1$以下のものを$1$に調整する際に削った元が$1$以下になる場合を考慮することでやや処理が複雑に見えることに注意が必要である。
乱数の生成
別名法は主に「①離散型確率分布の一様分布化」と「②乱数の生成」の$2$ステップで乱数生成を行うが、前項で「①離散型確率分布の一様分布化」について取り扱ったので当項では「②乱数の生成」に関して確認を行う。具体的には以下の手順で$1$つの乱数$X$を発生する。
$[1].$ 一様乱数$U \sim \mathrm{Uniform}(0,1)$に基づいて、$V=KU$を計算する。
$[2].$ $V$より大きい最小の整数を$k$とおき、$u \leftarrow k-V$の計算を行う。
$[3].$ $u \leq v_{k}$ならば$X \leftarrow k$、$u > v_{k}$であれば$X \leftarrow a_k$を生成する。
上記の手順の解釈にあたっては$0$〜$1$の値を取る$u$が$k$を発生させる確率が$v_{k}$、$a_{k}$を発生させる確率が$1-v_{k}$であることを元に考えれば良い。
別名法のPythonプログラムの作成
プログラムの基本形
前節の例に基づいてプログラムの基本形に関して確認を行う。まず、以下を実行することで「①離散型確率分布の一様分布化」を行うことができる。
import numpy as np
p = np.array([0.12, 0.24, 0.38, 0.16, 0.1])
K = p.shape[0]
v = p*K
x = np.arange(1,6,1)
a = np.arange(0,5,1)
G, S = v>=1., v<1.
while any(S):
for l in range(K):
if S[l]:
k = np.argmax(v)
v[k] -= 1-v[l]
a[l] = k
S[l] = False
if v[k]<1.:
S[k]=True
print("alias: {}".format(a))
print("probability: {}".format(v))・実行結果
alias: [2 1 1 2 2]
probability: [ 0.6 1. 0.8 0.8 0.5]次に、以下を実行することで「②乱数の生成」の手順に基づいて$N=1000$の乱数の生成を行うことができる。
import matplotlib.pyplot as plt
np.random.seed(0)
N = 1000
X = np.zeros(N)
for i in range(N):
V = np.random.rand()*K
k = np.int(V)+1
u = k-V
if u <= v[k-1]:
X[i] = k
else:
X[i] = a[k-1]+1
plt.subplot(121)
plt.bar(x,p,color="limegreen")
plt.title("probability distribution")
plt.subplot(122)
plt.hist(np.int8(X),bins=K,color="limegreen")
plt.title("histgram")
plt.show()・実行結果
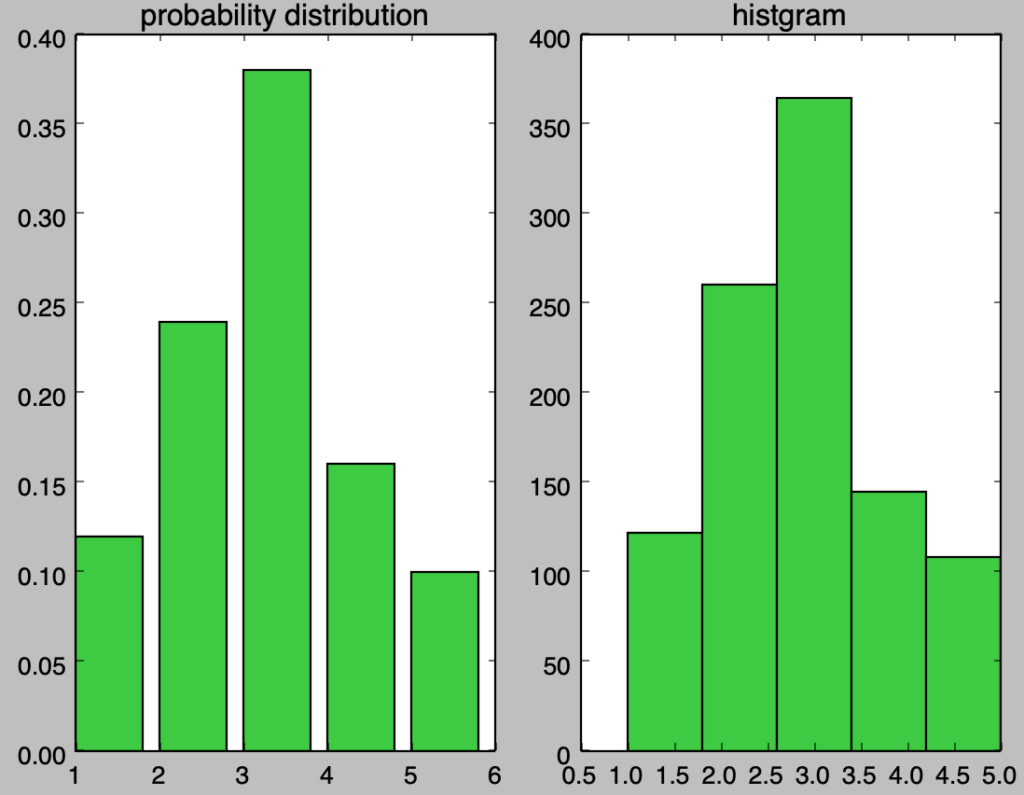
実行結果より、大元の確率分布の$p(X=1)=0.12, p(X=2)=0.24, p(X=3)=0.38, p(X=4)=0.16, p(X=5)=0.10$に概ね基づいて乱数が生成されたことが確認できる。
また、別名法を用いずに発生したサンプルに対しMCMCのように採択率を計算する方法もあり、こちらの方がシンプルではあるが、採択しなかった場合にサンプルを棄却することになり効率が良くない。逆に別名法では棄却する場合を他のサンプルの生成にあてることで計算効率を上げたと理解することもできる。

[…] […]