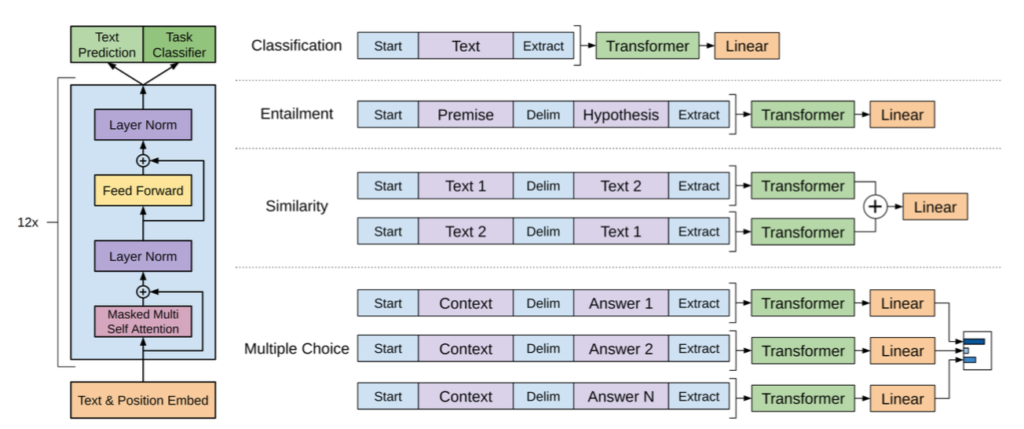
スコアを用いる生成モデルであるスコアベースモデル(SBM; Score Based Model)ではスコアの学習にあたってスコアマッチング(Score Matching)を行います。当記事ではデノイジングスコアマッチング(DSM; Denoising Score Matching)について取りまとめを行いました。
「拡散モデル ーデータ生成技術の数理(岩波書店)」の$1$章の「生成モデル」を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提知識
多次元正規分布
多次元正規分布の直感的な理解については下記で取り扱った。
多次元正規分布・ベイズの定理・周辺確率
$$
\large
\begin{align}
p(\mathbf{x}) &= \mathcal{N}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda}^{-1}) \\
p(\mathbf{y}|\mathbf{x}) &= \mathcal{N}(\mathbf{y}|\mathbf{A}\mathbf{x}+\mathbf{b},\mathbf{L}^{-1})
\end{align}
$$
上記のような確率分布$p(\mathbf{x})$と条件付き確率分布$p(\mathbf{y}|\mathbf{x})$を定義するとき、周辺分布$p(\mathbf{y})$は下記のように得られる。
$$
\large
\begin{align}
p(\mathbf{y}) = \mathcal{N}(\mathbf{x}|\mathbf{A}\mathbf{\mu} + \mathbf{b},\mathbf{L}^{-1}+\mathbf{A}\mathbf{\Lambda}^{-1}\mathbf{A}^{\mathrm{T}}) \quad (1.1)
\end{align}
$$
上記の詳しい導出は下記で取り扱った。
デノイジングスコアマッチング(DSM)
摂動後分布
サンプルに対応するベクトル$\mathbf{x}$に正規分布からのノイズベクトル$\epsilon \sim \mathcal{N}(\mathbf{0},\sigma^{2}I)$を加えた変数$\tilde{\mathbf{x}}$を下記のように定義する。
$$
\large
\begin{align}
\tilde{\mathbf{x}} = \mathbf{x} + \epsilon, \quad \epsilon \sim \mathcal{N}(\mathbf{0}, \sigma^{2}I) \quad (2.1)
\end{align}
$$
上記のノイズベクトル$\epsilon$を摂動、$\sigma$をノイズのスケールという。ここで条件付き確率$p_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x})$を下記のように定義する。
$$
\large
\begin{align}
p_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x}) = \mathcal{N}(\tilde{\mathbf{x}};\mathbf{x},\sigma^{2}I) = \frac{1}{(2 \pi \sigma^{2})^{d/2}} \exp{ \left[ -\frac{1}{2 \sigma^{2}}||\tilde{\mathbf{x}}-\mathbf{x}||^{2} \right] } \quad (2.2)
\end{align}
$$
さらに摂動後分布$p_{\sigma}(\bar{\mathbf{x}}$を周辺分布の式に基づいて下記のように定義する。
$$
\large
\begin{align}
p_{\sigma}(\tilde{\mathbf{x}}) = \int_{\mathbf{x} \in \mathbb{R}^{d}} p_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x}) p(\mathbf{x}) d \mathbf{x}
\end{align}
$$
上記の摂動後分布$p_{\sigma}(\tilde{\mathbf{x}})$は元の分布$p(\mathbf{x})$をぼかした分布になる。直感的には画像に平均フィルタを適用してぼかすのと同様に理解するとわかりやすい。
摂動後分布の解釈：$p(\mathbf{x})$が正規分布の場合
前項の解釈にあたって、$p(\mathbf{x})=\mathcal{N}(\mu,\Sigma)$を仮定する。このとき$(1.1)$式を用いて摂動後分布$p_{\sigma}(\tilde{\mathbf{x}})$は下記のように得られる。
$$
\large
\begin{align}
p_{\sigma}(\tilde{\mathbf{x}}) = \mathcal{N}(\mathbf{x}|\mu,\sigma^{2}I+\Sigma)
\end{align}
$$
上記より摂動後分布$p_{\sigma}(\tilde{\mathbf{x}})$は元の分布$p(\mathbf{x})$をぼかした分布であることが確認できる。
DSMの目的関数
デノイジングスコアマッチング(DSM; Denoising Score Matching)では下記のように定義する目的関数$J_{DSM_{p_{\sigma}}}(\theta)$を用いて学習を行う。
$$
\large
\begin{align}
J_{DSM_{p_{\sigma}}}(\theta) = \frac{1}{2} \mathbb{E}_{p_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x}) p(\mathbf{x})} \left[ || \nabla_{\tilde{\mathbf{x}}} \log{p_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x})} – s_{\theta}(\tilde{\mathbf{x}},\sigma)||^{2} \right] \quad (2.3)
\end{align}
$$
ここで$(2.2)$式より、$\nabla_{\tilde{\mathbf{x}}} \log{p_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x})}$は下記のように計算できる。
$$
\large
\begin{align}
\nabla_{\tilde{\mathbf{x}}} \log{p_{\sigma}(\tilde{\mathbf{x}}|\mathbf{x})} &= \nabla_{\tilde{\mathbf{x}}} \log{ \left( \frac{1}{(2 \pi \sigma^{2})^{d/2}} \exp{ \left[ -\frac{1}{2 \sigma^{2}}||\tilde{\mathbf{x}}-\mathbf{x}||^{2} \right] } \right) } \\
&= \nabla_{\tilde{\mathbf{x}}} \left( \log{ \frac{1}{(2 \pi \sigma^{2})^{d/2}} } – \nabla_{\tilde{\mathbf{x}}} \left[ \frac{1}{2 \sigma^{2}}||\tilde{\mathbf{x}}-\mathbf{x}||^{2} \right] \right) \\
&= 0 – \frac{1}{\sigma^{2}} (\tilde{\mathbf{x}}-\mathbf{x}) = -\frac{1}{\sigma^{2}} \epsilon \quad (2.4)
\end{align}
$$
$(2.1), \, (2.4)$式などを元に、$(2.3)$式は下記のように書き換えることができる。
$$
\large
\begin{align}
J_{DSM_{p_{\sigma}}}(\theta) = \frac{1}{2} \mathbb{E}_{\epsilon \sim \mathcal{N}(\mathbf{0},\sigma^{2}I), \, \mathbf{x} \sim p(\mathbf{x})} \left[ \left|\middle| -\frac{1}{\sigma^{2}} – s_{\theta}(\tilde{\mathbf{x}},\sigma) \middle|\right|^{2} \right] \quad (2.5)
\end{align}
$$
上記のように定義した$J_{DSM_{p_{\sigma}}}(\theta)$について下記が成立する。
$$
\large
\begin{align}
J_{ESM_{p_{\sigma}}}(\theta) = J_{DSM_{p_{\sigma}}}(\theta) + C \quad (2.6)
\end{align}
$$
$(2.6)$式の導出は当記事では省略しますが、「拡散モデル ーデータ生成技術の数理(岩波書店)」が詳しいので下記を参照ください。
