ブログ

当記事では$F(x,y)=0$のような陰関数形式の曲線の接線(tangent line)の方程式の公式に関して確認を行います。数Ⅱなどで$y=g(x)$の接線の公式は取り扱いますが、$F(x,y)=0$に関しても同様な数式に基づいて表されるので確認しておくと良いと思います。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$6$章「微分(多変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(11/06 18:58時点)

Amazon

$F(x,y)=0$の接線の方程式の計算

接線の方程式の公式

曲線$F(x,y)=0$に対して、下記のように偏微分を定義する。
$$
\large
\begin{align}
F_{x}(x,y) &= \frac{\partial F(x,y)}{\partial x} \\
F_{y}(x,y) &= \frac{\partial F(x,y)}{\partial y}
\end{align}
$$

このとき、$F(x,y)=0$上の点$(a,b)$に関して$F_{x}(a,b)=F_{y}(a,b)=0$が成立すれば$(a,b)$を曲線$F(x,y)=0$の特異点という。

一方で、$F_{x}(a,b) \neq 0$または$F_{y}(a,b) \neq 0$であれば点$(a,b)$は曲線$F(x,y)=0$の正則点という。ここで曲線$F(x,y)=0$上の正則点$(a,b)$における接線の方程式は下記のように表される。
$$
\large
\begin{align}
F_{x}(a,b)(x-a) + F_{y}(a,b)(y-b) = 0 \quad (1)
\end{align}
$$

多変数関数に関する合成関数の微分の使用例

以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。

基本例題$118$

以下、曲線$x^3 + y^3 = 1$上の点$\displaystyle \left( \frac{1}{\sqrt[3]{2}}, \frac{1}{\sqrt[3]{2}} \right)$における接線の方程式の導出を行う。

計算にあたって$F(x,y) = x^3+y^3-1 = 0$とおくと、偏微分$F_{x}(x,y), F_{y}(x,y)$はそれぞれ下記のように計算を行うことができる。
$$
\large
\begin{align}
F_{x}(x,y) &= 3x^2 \\
F_{y}(x,y) &= 3y^2
\end{align}
$$

よって、$\displaystyle F_{x} \left( \frac{1}{\sqrt[3]{2}}, \frac{1}{\sqrt[3]{2}} \right), F_{y} \left( \frac{1}{\sqrt[3]{2}}, \frac{1}{\sqrt[3]{2}} \right)$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
F_{x} \left( \frac{1}{\sqrt[3]{2}}, \frac{1}{\sqrt[3]{2}} \right) &= \frac{3}{\sqrt[3]{4}} \\
F_{y} \left( \frac{1}{\sqrt[3]{2}}, \frac{1}{\sqrt[3]{2}} \right) &= \frac{3}{\sqrt[3]{4}}
\end{align}
$$

したがって、下記のような接線の方程式を考えることができる。
$$
\large
\begin{align}
F_{x}(a,b)(x-a) + F_{y}(a,b)(y-b) &= 0 \\
\frac{3}{\sqrt[3]{4}} \left( x – \frac{1}{\sqrt[3]{2}} \right) + \frac{3}{\sqrt[3]{4}} \left( y – \frac{1}{\sqrt[3]{2}} \right) &= 0 \\
x + y – \frac{2}{\sqrt[3]{2}} &= 0 \\
x + y – 2^{1-1/3} &= 0 \\
x + y – \sqrt[3]{4} &= 0
\end{align}
$$

基本例題$119$

$1$変数関数の合成関数(composite function)の微分は媒介変数に関する微分の積で計算することができますが、多変数関数に合成関数の微分の考え方を適用する際は積と和を組み合わせて考える必要がありやや複雑です。当記事では多変数関数に関する合成関数の微分の計算法と具体例に関してまとめました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$6$章「微分(多変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(11/06 18:58時点)

Amazon

多変数関数に関する合成関数の微分の計算法

平面上の開領域$U$で定義された全微分可能関数$z=f(x,y)$を考える。さらに開区間$I$で定義された微分可能関数の$x=\psi(t), y=\phi(t)$を考える。また、${}^{\forall} t \in I$に関して$(\psi(t), \phi(t)) \in U$が成立すると仮定する。このとき、$z = f(\psi(t), \phi(t))$は$I$上で微分可能であり、導関数は下記のように得られる。
$$
\large
\begin{align}
\frac{d f(\psi(t), \phi(t))}{dt} &= \frac{\partial f(\psi(t), \phi(t))}{\partial \psi(t)} \frac{d \psi(t)}{dt} + \frac{\partial f(\psi(t), \phi(t))}{\partial \phi(t)} \frac{d \phi(t)}{dt} \\
&= \frac{\partial f(x, y)}{\partial x} \frac{d \psi(t)}{dt} + \frac{\partial f(x, y)}{\partial y} \frac{d \phi(t)}{dt}
\end{align}
$$

多変数関数に関する合成関数の微分の使用例

以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。

基本例題$111$

$$
\large
\begin{align}
f(x, y) &= \log{(x^2+xy+y^2+1)} \\
\psi(t) &= e^{t} + e^{-t}, \quad \phi(t) = e^{t} – e^{-t} \\
g(t) &= f(\psi(t), \phi(t))
\end{align}
$$

上記のように定めた$g(t)$に対し、以下$g'(t)$の計算を行う。$g'(t)$は$f(\psi(t), \phi(t))$を用いて下記のような式で表される。
$$
\large
\begin{align}
g'(t) &= \frac{d f(\psi(t), \phi(t))}{dt} \\
&= \frac{\partial f(\psi(t), \phi(t))}{\partial \psi(t)} \frac{d \psi(t)}{dt} + \frac{\partial f(\psi(t), \phi(t))}{\partial \phi(t)} \frac{d \phi(t)}{dt} \\
&= \frac{\partial f(x, y)}{\partial x} \frac{d \psi(t)}{dt} + \frac{\partial f(x, y)}{\partial y} \frac{d \phi(t)}{dt}
\end{align}
$$

ここで$\displaystyle \frac{\partial f(x, y)}{\partial x}, \frac{d \psi(t)}{dt}, \frac{\partial f(x, y)}{\partial y}, \frac{d \phi(t)}{dt}$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
\frac{\partial f(x, y)}{\partial x} &= \frac{\partial}{\partial x} (\log{(x^2+xy+y^2+1)}) \\
&= \frac{2x+y}{x^2+xy+y^2+1} \\
\frac{d \psi(t)}{dt} &= \frac{d}{dt}(e^{t} + e^{-t}) = e^{t} – e^{-t}
\end{align}
$$

$$
\large
\begin{align}
\frac{\partial f(x, y)}{\partial y} &= \frac{\partial}{\partial y} (\log{(x^2+xy+y^2+1)}) \\
&= \frac{x+2y}{x^2+xy+y^2+1} \\
\frac{d \phi(t)}{dt} &= \frac{d}{dt}(e^{t} – e^{-t}) = e^{t} + e^{-t}
\end{align}
$$

ここで$2x+y, x+2y, x^2+xy+y^2+1$は$t$を用いて下記のように表せる。
$$
\large
\begin{align}
2x+y &= 2(e^{t}+e^{-t}) + (e^{t}-e^{-t}) \\
&= 3e^{t} + e^{-t} \\
x+2y &= 2(e^{t}+e^{-t}) – (e^{t}-e^{-t}) \\
&= 3e^{t} – e^{-t} \\
x^2+xy+y^2+1 &= (e^{t}+e^{-t})^{2} + (e^{t}+e^{-t})(e^{t}-e^{-t}) + (e^{t}-e^{-t})^{2} + 1 \\
&= e^{2t} + \cancel{2} + \cancel{e^{-2t}} + e^{2t} – \cancel{e^{-2t}} + e^{2t} – \cancel{2} + e^{-2t} + 1 \\
&= 3e^{2t} + e^{-2t} + 1
\end{align}
$$

よって、$g'(t)$は下記のように導出できる。
$$
\large
\begin{align}
g'(t) &= \frac{\partial f(x, y)}{\partial x} \frac{d \psi(t)}{dt} + \frac{\partial f(x, y)}{\partial y} \frac{d \phi(t)}{dt} \\
&= \frac{2x+y}{x^2+xy+y^2+1}(e^{t} – e^{-t}) + \frac{x+2y}{x^2+xy+y^2+1}(e^{t} + e^{-t}) \\
&= \frac{1}{3e^{2t} + e^{-2t} + 1} \left[ (3e^{t} + e^{-t})(e^{t} – e^{-t}) + (3e^{t} – e^{-t})(e^{t} + e^{-t}) \right] \\
&= \frac{1}{3e^{2t} + e^{-2t} + 1} \left( 3e^{2t} – e^{-2t} + 3 – 1 + 3e^{2t} – e^{-2t} + 3 – 1 \right) \\
&= \frac{6e^{2t} – 2e^{-2t}}{3e^{2t} + e^{-2t} + 1}
\end{align}
$$

基本例題$112$

基本例題$113$

微分や偏微分の演算を表すにあたって、微分作用素(differential operator)・偏微分作用素を用いると簡略的に表すことができます。微分作用素はベクトルでの微分を表す際などによく用いられるので、当記事では微分作用素の定義や使用例に関して取りまとめを行いました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$6$章「微分(多変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(11/06 18:58時点)

Amazon

微分作用素・偏微分作用素の定義

$\displaystyle \frac{\partial}{\partial x}, \frac{\partial}{\partial y}$はそれぞれ関数に対して「微分・偏微分」の作用を施すものであることから微分作用素・偏微分作用素といわれる。よく用いられる微分作用素に下記のようなラプラス作用素がある。
$$
\large
\begin{align}
\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}
\end{align}
$$

上記は$2$変数のラプラス作用素である。このように微分作用素を定めることで演算の表記を簡略化することができる。

微分作用素・偏微分作用素の使用例

以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。

基本例題$124$

$$
\large
\begin{align}
D &= a \frac{\partial}{\partial x} + b \frac{\partial}{\partial y} \\
a, b & \in \mathbb{R}
\end{align}
$$

上記のように定めた偏微分作用素$D$に関して下記がそれぞれ成立する。

・$(1)$
$$
\large
\begin{align}
D(x^2y^3) &= a \frac{\partial}{\partial x}(x^2y^3) + b \frac{\partial}{\partial y}(x^2y^3) \\
&= 2axy^3 + 3bx^2y^2
\end{align}
$$

・$(2)$
$$
\large
\begin{align}
D(\sin{(x^2+y^2)}) &= a \frac{\partial}{\partial x}(\sin{(x^2+y^2)}) + b \frac{\partial}{\partial y}(\sin{(x^2+y^2)}) \\
&= a \cos{(x^2+y^2)} \cdot 2x + b \cos{(x^2+y^2)} \cdot 2y \\
&= 2 (ax+by) \cos{(x^2+y^2)}
\end{align}
$$

・$(3)$
$$
\large
\begin{align}
D(e^{x+y}) &= a \frac{\partial}{\partial x}(e^{x+y}) + b \frac{\partial}{\partial y}(e^{x+y}) \\
&= a e^{x+y} + b e^{x+y} = (a+b) e^{x+y}
\end{align}
$$

基本例題$125$

重要例題$074$

$$
\large
\begin{align}
\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}
\end{align}
$$

上記のようにラプラス作用素$\Delta$を定義する。ここで$x=r\sin{\theta}, y=r\cos{\theta}$のように変数変換を行うとき、$\Delta$は下記のように表せる。
$$
\large
\begin{align}
\Delta = \frac{\partial^2}{\partial r^2} + \frac{1}{r} \cdot \frac{\partial}{\partial r} + \frac{1}{r^2} \cdot \frac{\partial}{\partial \theta^2}
\end{align}
$$

以下では上記が成立することを示す。

$f(x,y)=f(r\cos{\theta},r\sin{\theta})=g(r,\theta)$とおく。このとき下記が成立する。
$$
\large
\begin{align}
\frac{\partial g}{\partial r} &= \frac{\partial f}{\partial x} \cos{\theta} + \frac{\partial f}{\partial y} \sin{\theta} \\
\frac{\partial g}{\partial \theta} &= -\frac{\partial f}{\partial x} r \sin{\theta} + \frac{\partial f}{\partial y} r \cos{\theta}
\end{align}
$$

また、下記も成立する。
$$
\large
\begin{align}
\frac{\partial^2 g}{\partial r^2} &= \frac{\partial^2 f}{\partial x^2} \cos^{2}{\theta} + 2 \frac{\partial f}{\partial x \partial y} \sin{\theta} \cos{\theta} + \frac{\partial^2 f}{\partial y^2} \sin^{2}{\theta} \\
\frac{\partial^2 g}{\partial \theta}^2 &= r^2 \left( \frac{\partial^2 f}{\partial x^2} \sin^{2}{\theta} – 2 \frac{\partial f}{\partial x \partial y} \sin{\theta} \cos{\theta} + \frac{\partial^2 f}{\partial y^2} \cos^{2}{\theta} \right) – r \left( \frac{\partial f}{\partial x} \cos{\theta} + \frac{\partial f}{\partial y}\sin{\theta} \right)
\end{align}
$$

したがって下記が成立する。
$$
\large
\begin{align}
& \frac{\partial^2 g}{\partial r^2} + \frac{1}{r} \cdot \frac{\partial g}{\partial r} + \frac{1}{r^2} \cdot \frac{\partial g}{\partial \theta^2} \\
&= \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}
\end{align}
$$

重積分(multi integral)の計算にあたって変数変換はよく用いられますが、ヤコビアン(Jacobian)の計算が出てくるなど計算がやや複雑です。そこで当記事では具体例の確認を通して重積分の変数変換の流れを抑えやすいように取りまとめを行いました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$7$章「積分(多変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(11/06 18:58時点)

Amazon

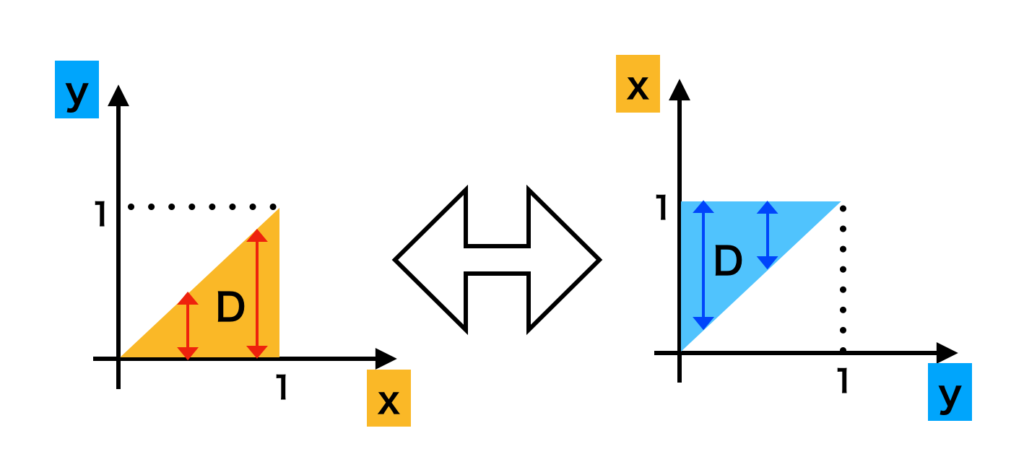
変数変換を用いた重積分の計算の流れ

一般的な形の有界閉領域の積分を取り扱う際に変数変換を用いることを検討すると良い。$x, y$による領域$D$に関して簡単に積分できない場合に、$D$に対応する長方形領域$E$を持つ$u, v$に変数変換を行うことで計算を簡略化できる。
$$
\large
\begin{align}
\int \int_{D} f(x,y) \, dx dy &= \int \int_{E} f(x(u,v),y(u,v)) |\det{J(u,v)}| \, du dv \\
\det{J(u,v)} &= \frac{\partial x(u,v)}{\partial u}\frac{\partial y(u,v)}{\partial v} – \frac{\partial y(u,v)}{\partial u}\frac{\partial x(u,v)}{\partial v}
\end{align}
$$

ここで$\det{J(u,v)}$の絶対値を考えることで、$u$と$v$の順序を入れ替えた積分の値を一致させることができることは抑えておくと良い。このことは行列式の列を入れ替えると符号を入れ替えた値になることと対応させて理解しておくと良い。

・参考
標準演習$100$選 変数変換

変数変換を用いた重積分(multi integral)の計算の流れの使用例

以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。

基本例題$132$

・$(1)$
$$
\large
\begin{align}
\int \int_{D} (x-y) e^{x+y} \, dx dy, \quad D = \{ (x,y) | 0 \leq x+y \leq 2, 0 \leq x-y \leq 2 \}
\end{align}
$$

上記に対して、下記のような変数変換を行うことを考える。
$$
\large
\begin{align}
u &= x+y \\
v &= x-y
\end{align}
$$

このとき、$x, y$は$u, v$を元に下記のように表せる。
$$
\large
\begin{align}
x &= \frac{u+v}{2} \\
y &= \frac{u-v}{2}
\end{align}
$$

よってヤコビ行列式$|\det{J}|$は下記のように計算できる。
$$
\large
\begin{align}
|\det{J}| &= \left| \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} – \frac{\partial x}{\partial v}\frac{\partial y}{\partial u} \right| \\
&= \left| \frac{1}{2}\left(-\frac{1}{2}\right) – \frac{1}{2}\frac{1}{2} \right| \\
&= \frac{1}{2}
\end{align}
$$

また、$0 \leq x+y \leq 2, 0 \leq x-y \leq 2$より、$0 \leq u \leq 2, 0 \leq v \leq 2$が対応する。ここで$E = \{ (u,v) | 0 \leq u \leq 2, 0 \leq v \leq 2 \}$とおく。

このとき下記のように重積分の計算を行うことができる。
$$
\large
\begin{align}
\int \int_{D} (x-y) e^{x+y} \, dx dy &= \int \int_{E} v e^{u} |\det{J}| \, du dv \\
&= \frac{1}{2} \int_{0}^{2} e^{u} du \cdot \int_{0}^{2} v dv \\
&= \frac{1}{2} \left[ e^{u} \right]_{0}^2 \cdot \left[ \frac{1}{2}v^2 \right]_{0}^{2} \\
&= \frac{1}{2^2}(e^2-1)(2^2-0) \\
&= e^2 – 1
\end{align}
$$

基本例題$133$

基本例題$134$

・$(1)$
$$
\large
\begin{align}
\int \int_{D} e^{x^2+y^2} \, dx dy, & \quad D = \{ (x,y) | y \geq 0, x^2+y^2 \leq a^2 \} \\
a > 0, & \quad a \in \mathbb{R}
\end{align}
$$

上記に対して下記のような変数変換を行うことを考える。
$$
\large
\begin{align}
x &= r \cos{\theta} \\
y &= r \sin{\theta}
\end{align}
$$

上記の変数変換に対し、ヤコビ行列式$|\det{J}|$は下記のように計算できる。
$$
\large
\begin{align}
|\det{J}| &= \left| \frac{\partial x}{\partial r}\frac{\partial y}{\partial \theta} – \frac{\partial x}{\partial \theta}\frac{\partial y}{\partial r} \right| \\
&= \left| \cos{\theta} \cdot r \cos{\theta} – (-r \sin{\theta}) \cdot \sin{\theta} \right| \\
&= r (\cos^{2}{\theta}+\sin^{2}{\theta}) = r
\end{align}
$$

また、$y \geq 0, x^2+y^2 \leq a^2$より、$0 \leq r \leq a, 0 \leq \theta \leq \pi$が対応する。ここで$E = \{ (r,\theta) | 0 \leq r \leq a, 0 \leq \theta \leq \pi \}$とおく。

このとき下記のように重積分の計算を行うことができる。
$$
\large
\begin{align}
\int \int_{D} e^{x^2+y^2} \, dx dy &= \int \int_{E} e^{r^2(\cos^{2}{\theta}+\sin^{2}{\theta})} |\det{J}| \, dr d \theta \\
&= \int \int_{E} r e^{r^2} \, dr d \theta \\
&= \int_{0}^{a} \int_{0}^{\pi} r e^{r^2} \, d \theta dr \\
&= \int_{0}^{a} \left[ r e^{r^2} \theta \right]_{\theta=0}^{\theta=\pi} dr \\
&= \int_{0}^{a} \pi r e^{r^2} dr \\
&= \frac{\pi}{2} \int_{0}^{a} (e^{r^2})’ dr \\
&= \frac{\pi}{2} \left[ e^{r^2} \right]_{0}^{a} \\
&= \frac{\pi}{2}(e^{a^2}-1)
\end{align}
$$

・$(2)$
$$
\large
\begin{align}
\int \int_{D} xy^2 \, dx dy, & \quad D = \{ (x,y) | x \geq 0, y \geq 0, x^2+y^2 \leq 1 \}
\end{align}
$$

上記に対して下記のような変数変換を行うことを考える。
$$
\large
\begin{align}
x &= r \cos{\theta} \\
y &= r \sin{\theta}
\end{align}
$$

上記の変数変換に対し、ヤコビ行列式$|\det{J}|$は下記のように計算できる。
$$
\large
\begin{align}
|\det{J}| &= \left| \frac{\partial x}{\partial r}\frac{\partial y}{\partial \theta} – \frac{\partial x}{\partial \theta}\frac{\partial y}{\partial r} \right| \\
&= \left| \cos{\theta} \cdot r \cos{\theta} – (-r \sin{\theta}) \cdot \sin{\theta} \right| \\
&= r (\cos^{2}{\theta}+\sin^{2}{\theta}) = r
\end{align}
$$

また、$y \geq 0, x^2+y^2 \leq 1$より、$\displaystyle 0 \leq r \leq 1, 0 \leq \theta \leq \frac{\pi}{2}$が対応する。ここで$\displaystyle E = \left\{ (r,\theta) | 0 \leq r \leq 1, 0 \leq \theta \leq \frac{\pi}{2} \right\}$とおく。

このとき下記のように重積分の計算を行うことができる。
$$
\large
\begin{align}
\int \int_{D} xy^2 \, dx dy &= \int \int_{E} r \cos{\theta} (r \sin{\theta})^2 |\det{J}| \, dr d \theta \\
&= \int_{0}^{1} r^4 dr \cdot \int_{0}^{\frac{\pi}{2}} \cos{\theta} \sin^{2}{\theta} \, d \theta dr \\
&= \int_{0}^{1} r^4 dr \cdot \int_{0}^{\frac{\pi}{2}} \frac{1}{3} (\sin^{3}{\theta})’ \, d \theta \\
&= \left[ \frac{1}{5} r^5 \right]_{0}^{1} \cdot \left[ \frac{1}{3} \sin^{3}{\theta} \right]_{0}^{\frac{\pi}{2}} \\
&= \frac{1}{5} \cdot \frac{1}{3} = \frac{1}{15}
\end{align}
$$

基本例題$135$

・$(1)$
$$
\large
\begin{align}
\int \int_{D} (x-y)^2 \sin{(x-y)} \, dx dy, \quad D = \left\{ (x,y) | 0 \leq x+y \leq \pi, -\frac{\pi}{2} \leq x-y \leq \frac{\pi}{2} \right\}
\end{align}
$$

・$(2)$
$$
\large
\begin{align}
\int \int_{D} \sqrt{x^2+y^2} \, dx dy, \quad D = \{ (x,y) | x^2+y^2 \leq 2x \}
\end{align}
$$

上記に対して下記のような変数変換を行うことを考える。
$$
\large
\begin{align}
x &= r \cos{\theta}, \, y = r \sin{\theta} \\
0 \leq & r \leq 2 \cos{\theta}, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}
\end{align}
$$

上記の変数変換に対し、ヤコビ行列式$|\det{J}|$は下記のように計算できる。
$$
\large
\begin{align}
|\det{J}| &= \left| \frac{\partial x}{\partial r}\frac{\partial y}{\partial \theta} – \frac{\partial x}{\partial \theta}\frac{\partial y}{\partial r} \right| \\
&= \left| \cos{\theta} \cdot r \cos{\theta} – (-r \sin{\theta}) \cdot \sin{\theta} \right| \\
&= r (\cos^{2}{\theta}+\sin^{2}{\theta}) = r
\end{align}
$$

ここで$\displaystyle E = \left\{ (r,\theta) | 0 \leq r \leq 2 \cos{\theta}, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \right\}$とおく。

このとき下記のように重積分の計算を行うことができる。
$$
\large
\begin{align}
\int \int_{D} \sqrt{x^2+y^2} \, dx dy &= \int \int_{E} \sqrt{r^2(\cos^{2}{\theta}+\sin^{2}{\theta})} |r| \, dr d \theta \\
&= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{0}^{2 \cos{\theta}} r^2 \, dr d \theta \\
&= \frac{1}{3} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left[ r^3 \right]_{r=0}^{r=2 \cos{\theta}} d \theta \\
&= \frac{8}{3} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^{3}{\theta} d \theta \\
&= \frac{2}{3} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\cos{3 \theta} + 3 \cos{\theta}) d \theta \\
&= \frac{4}{3} \int_{0}^{\frac{\pi}{2}} (\cos{3 \theta} + 3 \cos{\theta}) d \theta \\
&= \frac{4}{3} \left[ \frac{1}{3}\sin{3 \theta} + 3 \sin{\theta} \right]_{0}^{\frac{\pi}{2}} \\
&= \frac{4}{3} \left( -\frac{1}{3} + 3 \right) \\
&= \frac{4}{3} \times \frac{4}{3} = \frac{32}{9}
\end{align}
$$

途中計算では三倍角の公式の$\cos{3 \theta} = 4 \cos^{3}{\theta} – 3\cos{\theta}$を元に変形を行なった。三倍角の公式の導出に関しては下記で詳しく取り扱った。

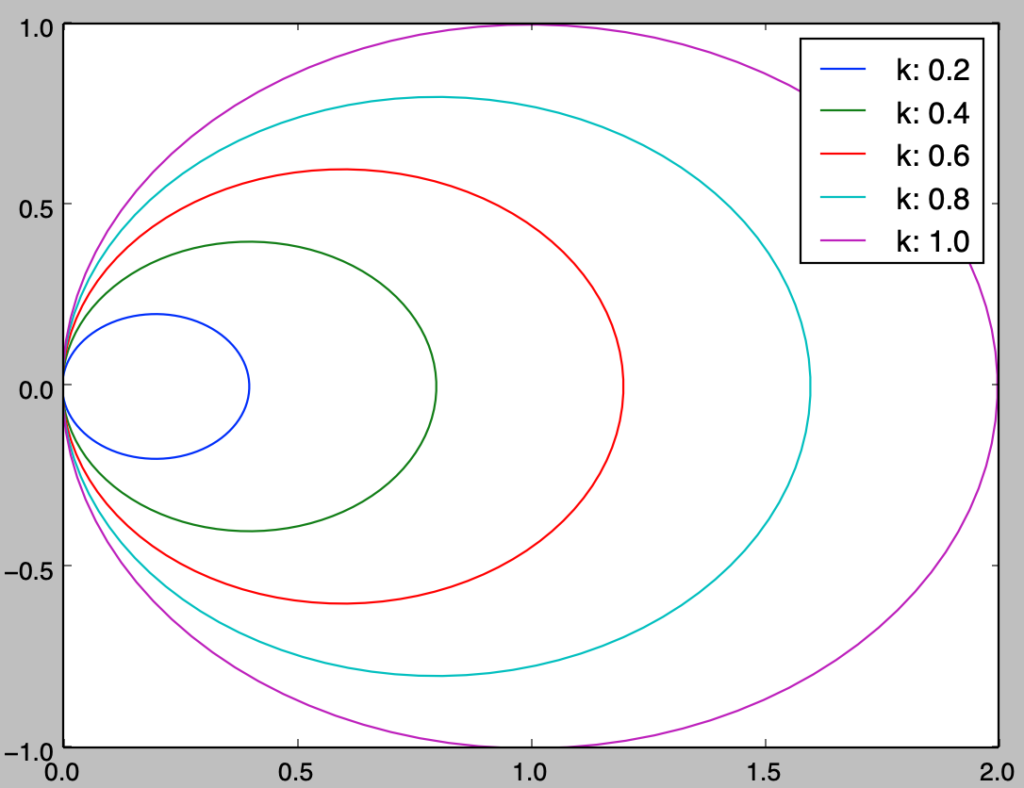
・$(2)$の変数変換の考察
$$
\large
\begin{align}
x &= r \cos{\theta}, \, y = r \sin{\theta} \\
0 \leq & r \leq 2 \cos{\theta}, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}
\end{align}
$$

以下、「上記の変数変換」と「不等式$x^2+y^2 \leq 2x$」の対応に関して確認を行う。

import numpy as np
import matplotlib.pyplot as plt

k = np.arange(0.2, 1.2, 0.2)
theta = np.linspace(-np.pi/2., np.pi/2., 100)

for i in range(k.shape[0]):
    r = 2*k[i]*np.cos(theta)
    x, y = r*np.cos(theta), r*np.sin(theta)

    plt.plot(x,y,label="k: {:.1f}".format(k[i]))

plt.legend()
plt.show()

・実行結果

上記の計算にあたって、kはrにかける倍率であり0.2, 0.4, 0.6, 0.8, 1.0の$5$つの倍率に関して描画を行なった。

基本例題$136$

累次積分(repeated integral)は「$1$変数関数の積分を繰り返すことで多重積分を計算する積分の計算法」です。当記事では累次積分の順序の入れ替えにあたっての注意事項に関して、具体例の計算過程の確認を通して取り扱いを行いました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$7$章「積分(多変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(11/06 18:58時点)

Amazon

曲線間領域における累次積分の計算の流れ

曲線領域における累次積分と同様に、積分領域を図的に把握したのちに積分順序に関して考えればよい。下記のような図の対応を考えると良い。

上記では$x$と$y$を入れ替えるにあたって対応がわかりやすいように$x$と$y$の反転を行った。

曲線間領域における累次積分の使用例

以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。

基本例題$130.(1)$

$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{0}^{x^3} f(x,y) dy \right) dx
\end{align}
$$

上記の積分の順序の入れ替えに関して以下考える。まず、上記の積分領域を$D$とおくと$D$は下記のように表せる。
$$
\large
\begin{align}
D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x^3 \}
\end{align}
$$

上記は$\{ (x,y) | 0 \leq y \leq 1, {}^{3}\sqrt{y} \leq x \leq 1 \}$と同じ領域であると考えることができる。よって、下記のように積分順序を入れ替えることができる。
$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{0}^{x^3} f(x,y) dy \right) dx = \int_{0}^{1} \left( \int_{{}^{3}\sqrt{y}}^{1} f(x,y) dx \right) dy
\end{align}
$$

基本例題$130.(2)$

$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{x^2}^{x} f(x,y) dy \right) dx
\end{align}
$$

上記の積分の順序の入れ替えに関して以下考える。まず、上記の積分領域を$D$とおくと$D$は下記のように表せる。
$$
\large
\begin{align}
D = \{ (x,y) | 0 \leq x \leq 1, x^2 \leq y \leq x \}
\end{align}
$$

上記は$\{ (x,y) | 0 \leq y \leq 1, y \leq x \leq \sqrt{y} \}$と同じ領域であると考えることができる。よって、下記のように積分順序を入れ替えることができる。
$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{x^2}^{x} f(x,y) dy \right) dx = \int_{0}^{1} \left( \int_{y}^{\sqrt{y}} f(x,y) dx \right) dy
\end{align}
$$

基本例題$130.(3)$

基本例題$131.(1)$

$$
\large
\begin{align}
\int \int_{D} x^3y \, dx dy, \quad D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x \}
\end{align}
$$

・$y$に関して先に積分
積分領域が$D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x \}$であるので、下記のように積分を行うことができる。
$$
\large
\begin{align}
\int \int_{D} x^3y \, dx dy &= \int_{0}^{1} \left( \int_{0}^{x} x^3y dy \right) dx \\
&= \int_{0}^{1} \left[ \frac{1}{2} x^3y^2 \right]_{y=0}^{y=x} dx \\
&= \int_{0}^{1} \frac{1}{2} x^5 dx \\
&= \left[ \frac{1}{12} x^6 \right]_{0}^{1} \\
&= \frac{1}{12}
\end{align}
$$

・$x$に関して先に積分
$D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x \} = \{ (x,y) | 0 \leq y \leq 1, y \leq x \leq 1 \}$が成立するので、下記のように積分を行うことができる。
$$
\large
\begin{align}
\int \int_{D} x^3y \, dx dy &= \int_{0}^{1} \left( \int_{y}^{1} x^3y dx \right) dy \\
&= \int_{0}^{1} \left[ \frac{1}{4} x^4y \right]_{x=y}^{x=1} dy \\
&= \int_{0}^{1} \frac{1}{4} (1-y^5) dy \\
&= \left[ \frac{y^2}{4 \cdot 2} – \frac{y^6}{4 \cdot 6} \right]_{0}^{1} \\
&= \frac{3-1}{8 \times 3} = \frac{1}{12}
\end{align}
$$

基本例題$131.(2)$

基本例題$131.(3)$

複素数を成分に持つ行列に対し、転置と複素共役を考えた行列を随伴行列(Adjoint matrix)といいます。随伴行列はエルミート行列(Hermitian matrix)の定義などの際にも用いられます。当記事では随伴行列の定義と性質に関して取りまとめを行いました。
作成にあたっては「チャート式シリーズ 大学教養 線形代数」の第$7$章の「内積」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 線形代数 (チャート式・シリーズ)

3,080円(11/06 16:22時点)

Amazon

随伴行列の定義

複素数を成分に持つ行列$A$に関して随伴行列(Adjoint matrix)を$A = \overline{A^{\mathrm{T}}}$のように定める。$A=(a_{ij})$のように表記するなら$A^{*}=(\overline{a_{ji}})$のように表せる。

随伴行列の性質

以下、「チャート式シリーズ 大学教養 線形代数」の例題の確認を行う。

基本例題$143.(1)$

行列$A$の各要素の複素共役を取った行列を$\overline{A}$と表す。このとき、複素共役と転置の交換が可能であることから$\overline{A}^{\mathrm{T}}=\overline{A^{\mathrm{T}}}$が成立する。よって$A^{*}=\overline{A^{\mathrm{T}}}$に関して下記のように考えることができる。
$$
\large
\begin{align} (A^{*})^{*} &= \overline{(A^{*})^{\mathrm{T}}} = \overline{(\overline{A^{\mathrm{T}}})^{\mathrm{T}}} \\
&= \overline{\overline{(A^{\mathrm{T}})^{\mathrm{T}}}} = A
\end{align}
$$

上記より、$(A^{*})^{*}=A$が成り立つ。

基本例題$143.(2)$

$A=(a_{ij}), B=(b_{ij})$とおく。このとき$(A+B)^{*}$の$(i,j)$成分の$((A+B)^{*})_{ij}$は下記のように表せる。
$$
\large
\begin{align}
((A+B)^{*})_{ij} &= \overline{a_{ji}+b_{ji}} \\
&= \overline{a_{ji}} + \overline{b_{ji}} \\
&= (A^{*})_{ij} + (B^{*})_{ij}
\end{align}
$$

上記より、$(A+B)^{*}=A^{*}+B^{*}$が成立する。

基本例題$143.(3)$

基本例題$143.(4)$

基本例題$143.(5)$

複素数を成分に持つ行列を考える際に成分が実数のみの場合の転置行列と同様の取り扱いをする際にエルミート行列(Hermitian matrix)が出てくることがあります。当記事ではエルミート行列の定義と性質に関して演習などを通して具体的に取りまとめを行いました。
作成にあたっては「チャート式シリーズ 大学教養 線形代数」の第$7$章「内積」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 線形代数 (チャート式・シリーズ)

3,080円(11/06 16:22時点)

Amazon

エルミート行列の概要

$n$次正方行列$A=(a_{ij})$を考え、$a_{ij}$の複素共役を$\overline{a_{ij}}$のように定める。このとき$a_{ij}=\overline{a_{ji}}$が成立する場合$A$はエルミート行列であるといい、$A^{*}=A$のように表す。

対角成分に関しては$a_{ii}=\overline{a_{ii}}$が成立するので、エルミート行列の対角成分が全て実数であることも抑えておくと良い。

エルミート行列の性質・行列式

以下、「チャート式シリーズ 大学教養 線形代数」の例題の確認を行う。

基本例題$144$

・$(1)$
行列$A, B$がエルミート行列である場合、下記が成り立つ。
$$
\large
\begin{align}
A^{*} &= A \\
B^{*} &= B
\end{align}
$$

よって下記が成立する。
$$
\large
\begin{align}
(A+B)^{*} &= A^{*} + B^{*} \\
&= A + B
\end{align}
$$

よって$A,B$がエルミートであるときは$A+B$もエルミート行列であると考えられる。

・$(2)$
$A=(a_{ij})$のように表すとき、行列$A$がエルミート行列であるなら$a_{ij}=\overline{a_{ji}}$が成立する。ここで$k \in \mathbb{R}$に関して下記が成立する。
$$
\large
\begin{align}
k a_{ij} = k \overline{a_{ji}} &= \overline{k a_{ji}}
\end{align}
$$

上記より$(kA^{*})=kA$であるので、行列$A$がエルミート行列であるなら$kA$もエルミート行列である。

基本例題$145$

以下、エルミート行列$A$の行列式$\det{(A)}$が実数であることを示す。$A$がエルミート行列であることから$A=A^{*}$であるので下記が成立する。
$$
\large
\begin{align}
\det{(A)} = \det{(A^{*})} \quad (1)
\end{align}
$$

また、$\det{(A^{*})}$に関して下記が成立する。
$$
\large
\begin{align}
\det{(A^{*})} = \overline{\det{(A)}} \quad (2)
\end{align}
$$

$(1), (2)$より下記が成立する。
$$
\large
\begin{align}
\det{(A)} = \overline{\det{(A)}}
\end{align}
$$

上記が成立することより$\det{(A)}$が実数であると考えることができる。

累次積分(repeated integral)は「$1$変数関数の積分を繰り返すことで多重積分を計算する積分の計算法」です。累次積分を用いることで多重積分を$1$変数の積分に帰着することが可能です。当記事では曲線間領域における累次積分の計算の流れとその具体例に関して取り扱いました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$7$章「積分(多変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(11/06 18:58時点)

Amazon

曲線間領域における累次積分の計算の流れ

閉区間$a \leq x \leq b$で定義された連続関数$y = \phi(x), y = \psi(x)$に関して、全ての$x$について$\phi(x) \leq \psi(x)$が成立すると仮定する。このとき領域$D = { (x,y)|a \leq x \leq b, \psi(x) \leq y \leq \phi(x) }$で定義される連続関数$f(x,y)$に関して下記が成立する。
$$
\large
\begin{align}
\int \int_{D} \sin{(x+y)} dx dy = \int_{a}^{b} \int_{\phi(x)}^{\psi(x)} f(x,y) dy dx
\end{align}
$$

曲線間領域における累次積分の使用例

以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。

基本例題$128.(1)$

$$
\large
\begin{align}
\int \int_{D} \sin{(x+y)} dx dy, \quad D = \{ (x,y)|x \geq 0, y \geq 0, x+y \leq \pi \}
\end{align}
$$

$x+y \leq \pi$より、$x \leq \pi-y$が成立する。ここで$x \geq 0, y \geq 0$も成立するので、$x$の定義域は$0 \leq x \leq \pi$のように考えることができる。また、$y \geq 0, x+y \leq \pi$より、$0 \leq y \leq \pi-x$が同様に成立するが、ここで$\psi(x)=0, \phi(x)=\pi-x$のようにおくことを考える。このとき$\psi(x) \leq y \leq \phi(x)$が成立する。よって、積分領域$D$に関して下記が成り立つ。
$$
\begin{align}
D = \{ (x,y)|x \geq 0, y \geq 0, x+y \leq \pi \} & \iff D = \{ (x,y)|0 \leq x \leq \pi, \psi(x) \leq y \leq \phi(x) \} \\
\psi(x) &= 0 \\
\phi(x) &= \pi-x
\end{align}
$$

よって、重積分は下記のように計算できる。
$$
\large
\begin{align}
\int \int_{D} \sin{(x+y)} dx dy &= \int_{0}^{\pi} \int_{\psi(x)}^{\phi(x)} \sin{(x+y)} dy dx \\
&= \int_{0}^{\pi} \left[-\cos{(x+y)}\right]_{0}^{\pi-x} dx \\
&= \int_{0}^{\pi} (\cos{x} – \cos{(\cancel{x}+\pi-\cancel{x})}) dx \\
&= \int_{0}^{\pi} (\cos{x} – (-1)) dx \\
&= \int_{0}^{\pi} (\cos{x} + 1) dx \\
&= \left[ \sin{x}+x \right]_{0}^{\pi} \\
&= \pi
\end{align}
$$

基本例題$128.(2)$

$$
\large
\begin{align}
\int \int_{D} (x+y) dx dy, \quad D = \{ (x,y)|x \leq y \leq 2-x^2 \}
\end{align}
$$

$x \leq 2-x^2$は、$(x+2)(x-1) \leq 0$のように変形できるので、$x$の定義域は$-2 \leq x \leq 1$のように考えることができる。また、$x \leq y \leq 2-x^2$が同様に成立するが、ここで$\psi(x)=x, \phi(x)=2-x^2$のようにおくことを考える。このとき$\psi(x) \leq y \leq \phi(x)$が成立する。よって、積分領域$D$に関して下記が成り立つ。
$$
\begin{align}
D = \{ (x,y)|x \leq y \leq 2-x^2 \} & \iff D = \{ (x,y)|0 \leq x \leq \pi, \psi(x) \leq y \leq \phi(x) \} \\
\psi(x) &= x \\
\phi(x) &= 2-x^2
\end{align}
$$

よって、重積分は下記のように計算できる。
$$
\large
\begin{align}
\int \int_{D} (x+y) dx dy &= \int_{-2}^{1} \int_{\psi(x)}^{\phi(x)} (x+y) dy dx \\
&= \int_{-2}^{1} \left[ xy + \frac{1}{2}y^2 \right]_{y=x}^{y=2-x^2} dx \\
&= \int_{-2}^{1} \left[ x(2-x^2) + \frac{1}{2}(2-x^2)^2 – \left( x^2 + \frac{1}{2}x^2 \right) \right] dx \\
&= \int_{-2}^{1} \left( \frac{1}{2}x^4 – x^3 – \frac{7}{2}x^2 + 2x + 2 \right) dx \\
&= \left[ \frac{1}{10}x^5 – \frac{1}{4}x^4 – \frac{7}{6}x^3 + x^2 + 2x \right]_{-2}^{1} \\
&= \left( \frac{1}{10} – \frac{1}{4} – \frac{7}{6} + 1 + 2 \right) – \left( \frac{32}{10} – 4 – \frac{56}{6} + 4 – 4 \right) \\
&= \frac{33}{10} – \frac{1}{4} – \frac{63}{6} + 3 + 4 \\
&= \frac{66-5-210+140}{20} = -\frac{9}{20}
\end{align}
$$

基本例題$128.(3)$

$$
\large
\begin{align}
\int \int_{D} x^2 y dx dy, \quad D = \{ (x,y)| x^2 + y^2 \leq 1, y \geq 0 \}
\end{align}
$$

重要例題$077.(1)$

重要例題$077.(2)$