累次積分(repeated integral)は「$1$変数関数の積分を繰り返すことで多重積分を計算する積分の計算法」です。当記事では累次積分の順序の入れ替えにあたっての注意事項に関して、具体例の計算過程の確認を通して取り扱いを行いました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$7$章「積分(多変数)」を主に参考にしました。
・数学まとめ
https://www.hello-statisticians.com/math_basic
Contents
曲線間領域における累次積分の計算の流れ
曲線領域における累次積分と同様に、積分領域を図的に把握したのちに積分順序に関して考えればよい。下記のような図の対応を考えると良い。
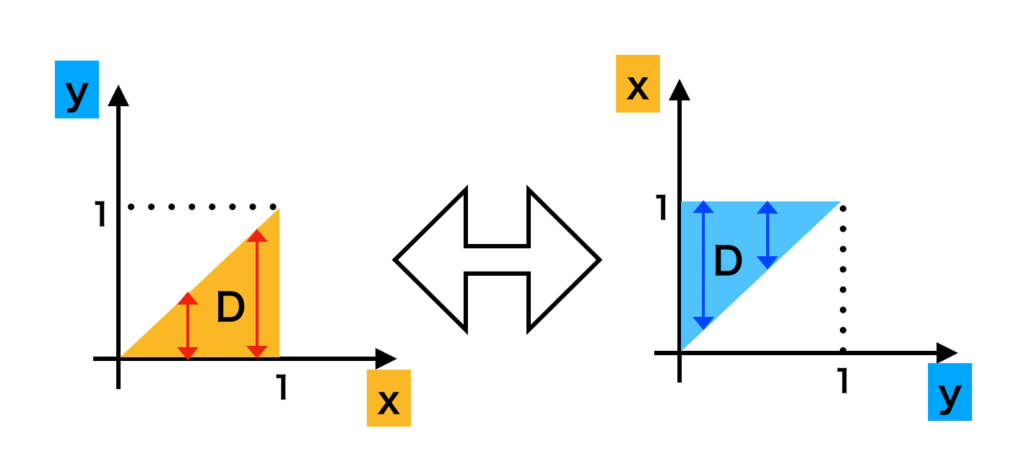
上記では$x$と$y$を入れ替えるにあたって対応がわかりやすいように$x$と$y$の反転を行った。
曲線間領域における累次積分の使用例
以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。
基本例題$130.(1)$
$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{0}^{x^3} f(x,y) dy \right) dx
\end{align}
$$
上記の積分の順序の入れ替えに関して以下考える。まず、上記の積分領域を$D$とおくと$D$は下記のように表せる。
$$
\large
\begin{align}
D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x^3 \}
\end{align}
$$
上記は$\{ (x,y) | 0 \leq y \leq 1, {}^{3}\sqrt{y} \leq x \leq 1 \}$と同じ領域であると考えることができる。よって、下記のように積分順序を入れ替えることができる。
$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{0}^{x^3} f(x,y) dy \right) dx = \int_{0}^{1} \left( \int_{{}^{3}\sqrt{y}}^{1} f(x,y) dx \right) dy
\end{align}
$$
基本例題$130.(2)$
$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{x^2}^{x} f(x,y) dy \right) dx
\end{align}
$$
上記の積分の順序の入れ替えに関して以下考える。まず、上記の積分領域を$D$とおくと$D$は下記のように表せる。
$$
\large
\begin{align}
D = \{ (x,y) | 0 \leq x \leq 1, x^2 \leq y \leq x \}
\end{align}
$$
上記は$\{ (x,y) | 0 \leq y \leq 1, y \leq x \leq \sqrt{y} \}$と同じ領域であると考えることができる。よって、下記のように積分順序を入れ替えることができる。
$$
\large
\begin{align}
\int_{0}^{1} \left( \int_{x^2}^{x} f(x,y) dy \right) dx = \int_{0}^{1} \left( \int_{y}^{\sqrt{y}} f(x,y) dx \right) dy
\end{align}
$$
基本例題$130.(3)$
基本例題$131.(1)$
$$
\large
\begin{align}
\int \int_{D} x^3y \, dx dy, \quad D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x \}
\end{align}
$$
・$y$に関して先に積分
積分領域が$D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x \}$であるので、下記のように積分を行うことができる。
$$
\large
\begin{align}
\int \int_{D} x^3y \, dx dy &= \int_{0}^{1} \left( \int_{0}^{x} x^3y dy \right) dx \\
&= \int_{0}^{1} \left[ \frac{1}{2} x^3y^2 \right]_{y=0}^{y=x} dx \\
&= \int_{0}^{1} \frac{1}{2} x^5 dx \\
&= \left[ \frac{1}{12} x^6 \right]_{0}^{1} \\
&= \frac{1}{12}
\end{align}
$$
・$x$に関して先に積分
$D = \{ (x,y) | 0 \leq x \leq 1, 0 \leq y \leq x \} = \{ (x,y) | 0 \leq y \leq 1, y \leq x \leq 1 \}$が成立するので、下記のように積分を行うことができる。
$$
\large
\begin{align}
\int \int_{D} x^3y \, dx dy &= \int_{0}^{1} \left( \int_{y}^{1} x^3y dx \right) dy \\
&= \int_{0}^{1} \left[ \frac{1}{4} x^4y \right]_{x=y}^{x=1} dy \\
&= \int_{0}^{1} \frac{1}{4} (1-y^5) dy \\
&= \left[ \frac{y^2}{4 \cdot 2} – \frac{y^6}{4 \cdot 6} \right]_{0}^{1} \\
&= \frac{3-1}{8 \times 3} = \frac{1}{12}
\end{align}
$$
