ブログ

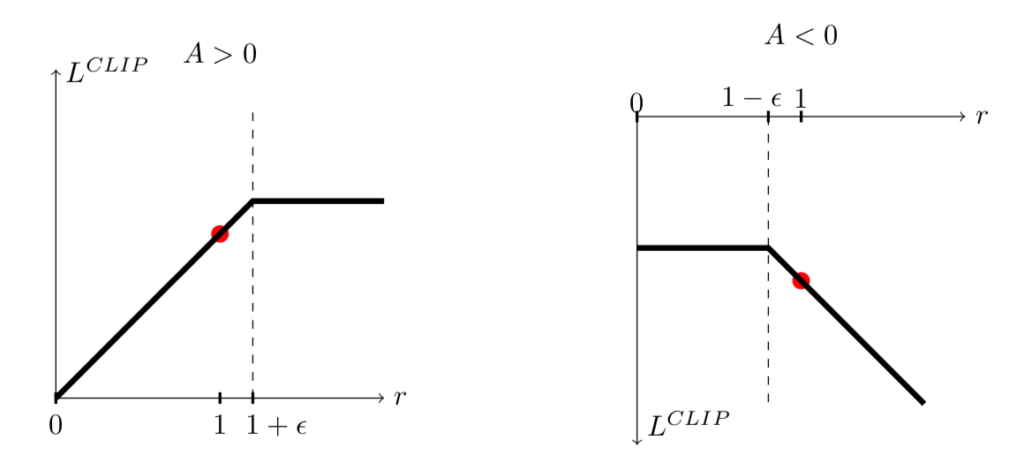
「データサイエンス 数学ストラテジスト 上級」はデータサイエンスの基盤である、確率・統計、線形代数、微積分、機械学習、プログラミングなどを取り扱う資格試験です。当記事では「日本数学検定協会」作成の「公式問題集」の演習問題$11$〜$20$の解答例を取り扱いました。

・数学検定まとめ
https://www.hello-statisticians.com/math_certificate

演習問題

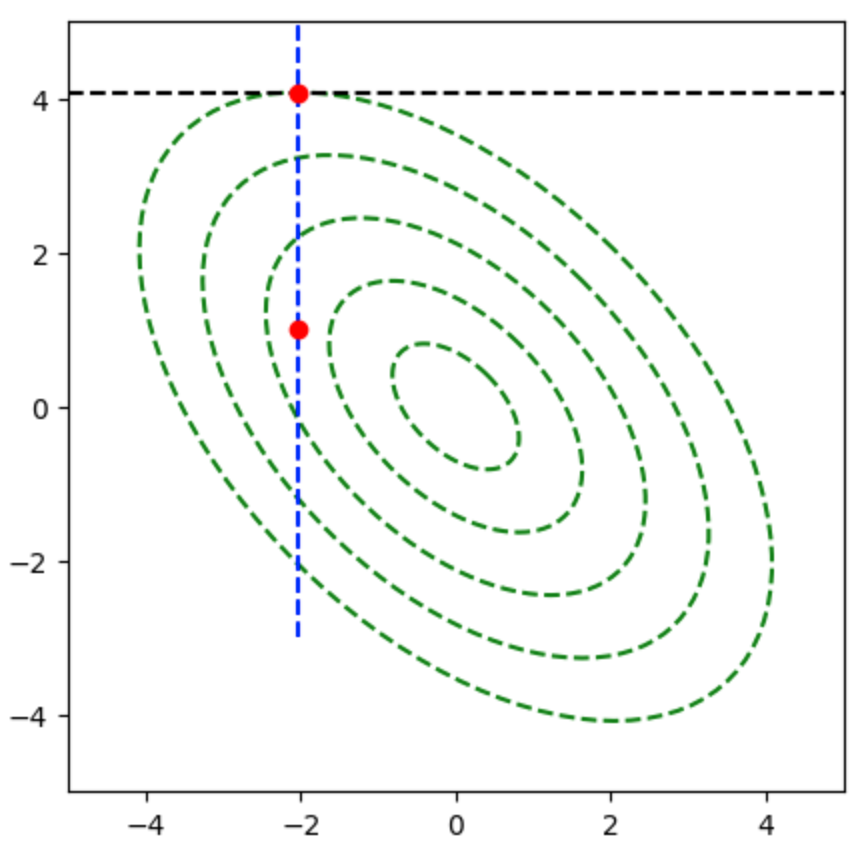
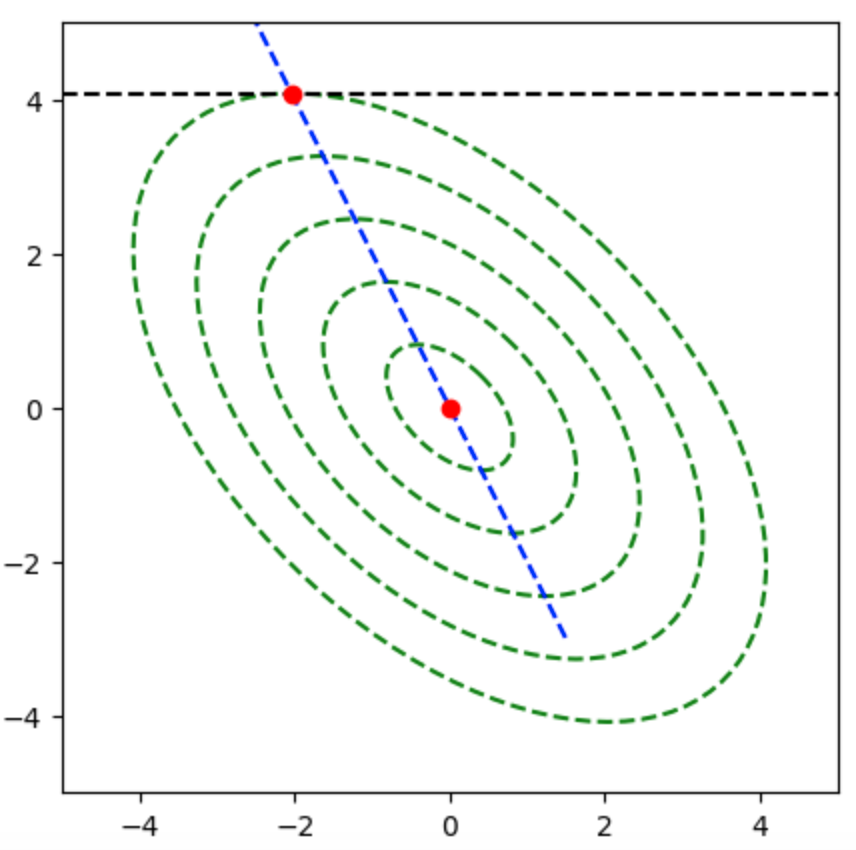
Q.11

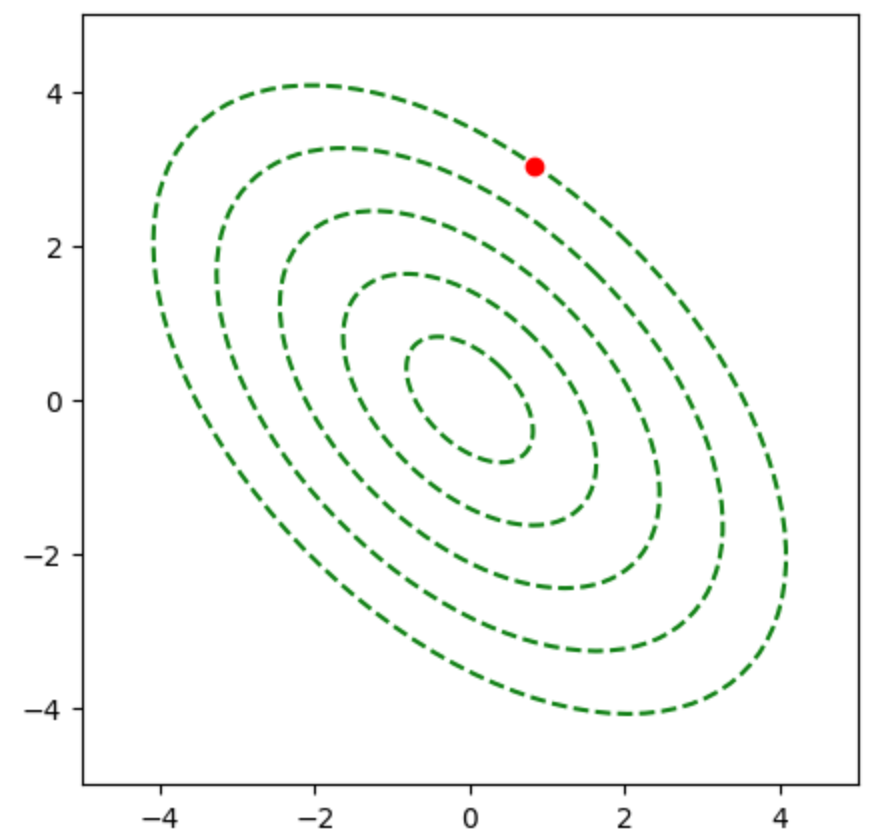
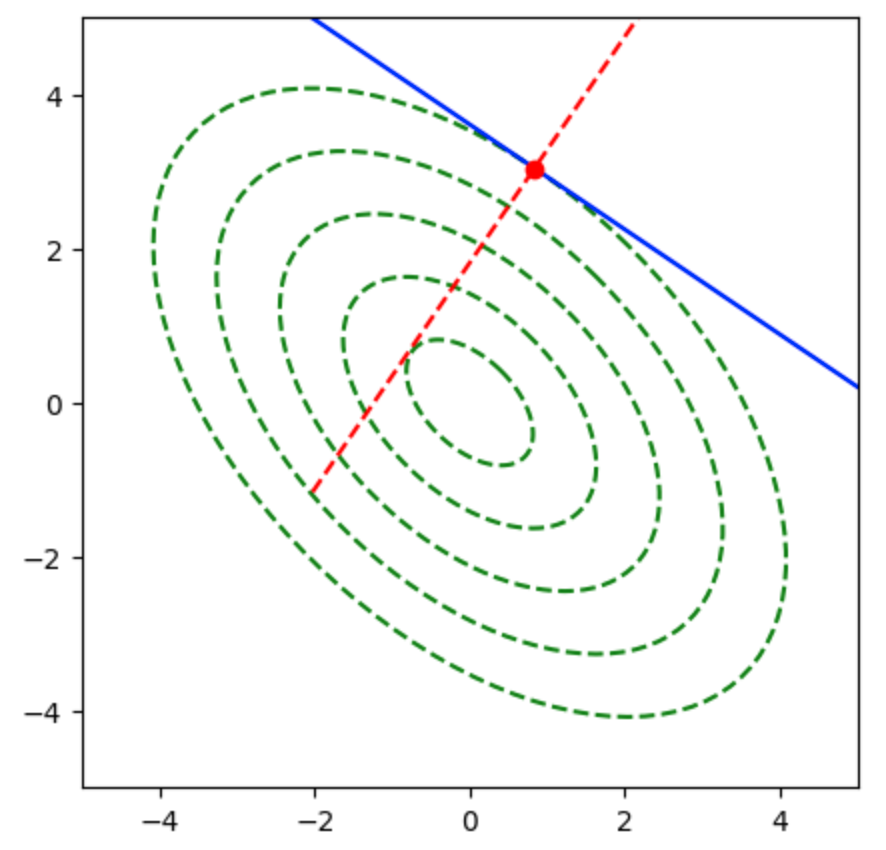
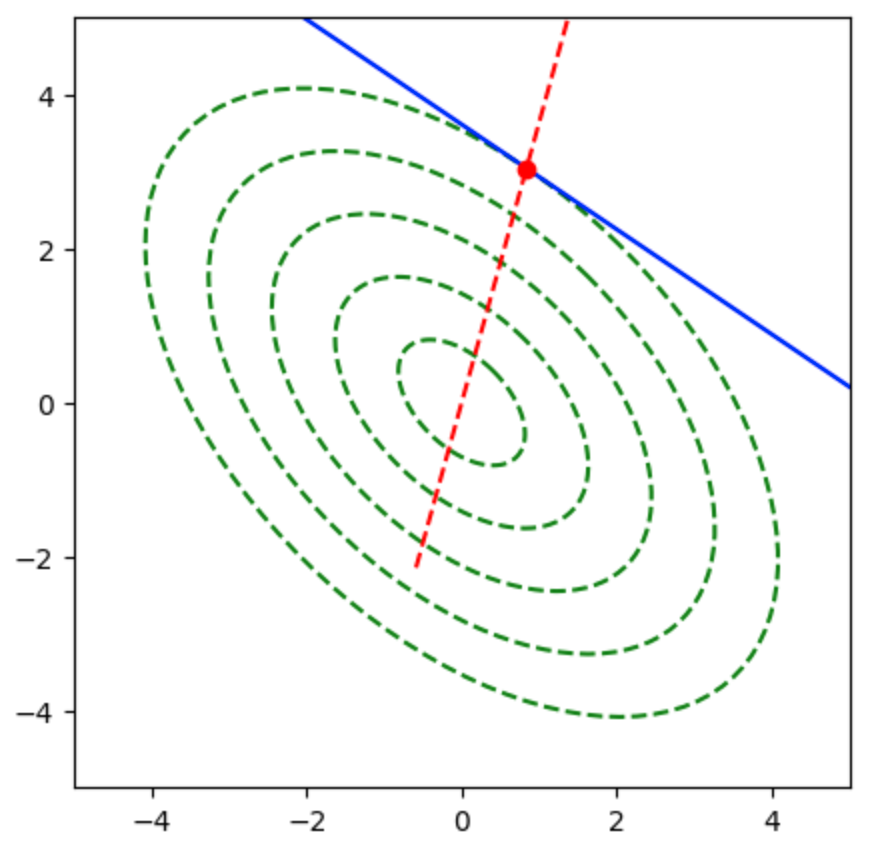
$\overrightarrow{AB}$と$\overrightarrow{OH}$はそれぞれ下記のように表すことができる。
$$
\large
\begin{align}
\overrightarrow{AB} &= \overrightarrow{OB} – \overrightarrow{OA} \\
\overrightarrow{OH} &= t \overrightarrow{OA} + (1-t) \overrightarrow{OB}
\end{align}
$$

ここで$\overrightarrow{AB} \perp \overrightarrow{OH}$であるので、$\overrightarrow{AB} \cdot \overrightarrow{OH} = 0$が成立するが、下記のように変形できる。
$$
\large
\begin{align}
\overrightarrow{AB} \cdot \overrightarrow{OH} &= 0 \\
(\overrightarrow{OB} – \overrightarrow{OA}) \cdot (t \overrightarrow{OA} + (1-t) \overrightarrow{OB}) &= 0 \\
t &= \frac{70}{127}
\end{align}
$$

よって、$\overrightarrow{OH}$は下記のように表すことができる。
$$
\large
\begin{align}
\overrightarrow{OH} = \frac{70}{127} \vec{a} + \frac{57}{127} \vec{b}
\end{align}
$$

上記より$(4)$が正しい。

Q.12

下記のように式変形を行える。
$$
\large
\begin{align}
\lim_{n \to \infty} \left[ \log_{10}{(n+100)} – \log_{10}{(1000n+1)} \right] &= \lim_{n \to \infty} \log_{10}{\frac{n+100}{1000n+1}} \\
&= \lim_{n \to \infty} \log_{10}{\frac{1+100/n}{1000+1/n}} \\
&= \log_{10}{\frac{1}{1000}} \\
&= \log_{10}{10^{-3}} \\
&= -3
\end{align}
$$

上記より$(5)$が正しい。

Q.13

$$
\large
\begin{align}
y = \frac{6}{(e^{x}+1)(e^{x}+3)}
\end{align}
$$

$e^{x}>0$より、$0 \leq x \leq 1$で$y>0$である。よって、図形の面積を$S$とおくと、$S$は下記のように立式できる。
$$
\large
\begin{align}
S = \int_{0}^{1} \frac{6}{(e^{x}+1)(e^{x}+3)} dx \quad [1]
\end{align}
$$

上記に対し、$t=e^{x}$のような変数変換を行う。このとき$\displaystyle \frac{dt}{dx}=e^{x}$より、$\displaystyle \frac{dt}{t}=dx$が成立する。また、$x$と$t$の区間は下記のように対応する。

$x$	$0 \longrightarrow 1$
$t$	$1 \longrightarrow e$

よって$[1]$式は下記のように値を得ることができる。
$$
\large
\begin{align}
S &= \int_{0}^{1} \frac{6}{(e^{x}+1)(e^{x}+3)} dx \quad [1] \\
&= \int_{1}^{e} \frac{6}{t(t+1)(t+3)} dt \\
&= \int_{1}^{e} \left[ \frac{2}{t} – \frac{3}{t+1} + \frac{1}{t+3} \right] dt \\
&= \left[ 2\log{|t|} – 3\log{|t+1|} + \log{|t+3|} \right]_{1}^{e} \\
&= \left( 2\log{e} – 3\log{(e+1)} + \log{(e+3)} \right) – \left( 2\log{1} – 3\log{(1+1)} + \log{(1+3)} \right) \\
&= 2 – 3\log{(e+1)} + \log{(e+3)} + \log{2}
\end{align}
$$

上記より$(3)$が正しい。

・解説
途中計算では下記のような部分分数分解を行いました。
$$
\large
\begin{align}
\frac{6}{t(t+1)(t+3)} = \frac{2}{t} – \frac{3}{t+1} + \frac{1}{t+3}
\end{align}
$$

上記の分解を発見するにあたっては、$\displaystyle \frac{6}{t(t+1)(t+3)} = \frac{a}{t} + \frac{b}{t+1} + \frac{c}{t+3}$とおき、両辺が一致するように$a, b, c$の値を得れば良いです。
$$
\large
\begin{align}
\frac{a}{t} + \frac{b}{t+1} + \frac{c}{t+3} &= \frac{a(t+1)(t+2) + bt(t+3) + ct(t+1)}{t(t+1)(t+3)} \\
&= \frac{(a+b+c)t^{2} + (4a+3b+c)t + 3a}{t(t+1)(t+3)}
\end{align}
$$

上記より$a+b+c=0, 4a+3b+c=0, 3a=6$が成立するので、$a=2, b=-3, c=1$を得ることができます。

・解説
部分分数分解は下記で詳しく取り扱いました。

部分分数分解(partial fraction decomposition)の解法まとめ

Q.14

$$
\large
\begin{align}
f(x) = \int_{0}^{x} f(t) \sin{(x-t)} dt + ax + b \quad [1]
\end{align}
$$

$\sin{(x-t)} = \sin{x}\cos{t} – \cos{x}\sin{t}$より、$[1]$式は下記のように変形できる。
$$
\large
\begin{align}
f(x) &= \int_{0}^{x} f(t) \sin{(x-t)} dt + ax + b \quad [1] \\
&= \int_{0}^{x} f(t) (\sin{x}\cos{t} – \cos{x}\sin{t}) dt + ax + b \\
&= \sin{x} \int_{0}^{x} f(t) \cos{t} dt – \cos{x} \int_{0}^{x} f(t) \sin{t} dt + ax + b \quad [2]
\end{align}
$$

$[2]$式の両辺を$x$で微分すると下記が得られる。
$$
\large
\begin{align}
f'(x) &= \left[ \sin{x} \int_{0}^{x} f(t) \cos{t} dt – \cos{x} \int_{0}^{x} f(t) \sin{t} dt + ax + b \right] \quad [2]’ \\
&= \cos{x} \int_{0}^{x} f(t) \cos{t} dt + \cancel{f(x)\sin{x}\cos{x}} + \sin{x} \int_{0}^{x} f(t) \sin{t} dt – \cancel{f(x)\sin{x}\cos{x}} + a \\
&= \cos{x} \int_{0}^{x} f(t) \cos{t} dt + \sin{x} \int_{0}^{x} f(t) \sin{t} dt + a
\end{align}
$$

上記の両辺を$x$で微分すると下記が得られる。
$$
\large
\begin{align}
f^{”}(x) &= -\sin{x} \int_{0}^{x} f(t) \cos{t} dt + f(x) \cos^{2}{x} + \cos{x} \int_{0}^{x} f(t) \sin{t} dt + f(x) \sin^{2}{x} \\
&= – \left[ \sin{x} \int_{0}^{x} f(t) \cos{t} dt – \cos{x} \int_{0}^{x} f(t) \sin{t} dt \right] + (\cos^{2}{x} + \sin^{2}{x})f(x) \\
&= -(f(x) – ax – b) + f(x) = ax + b
\end{align}
$$

$f^{”}(x) = ax+b$の両辺を$x$で積分すると下記が得られる。
$$
\large
\begin{align}
f'(x) = \frac{a}{2}x^{2} + bx + C_1
\end{align}
$$

ここで$f'(0)=a$より、$C_1=a$が得られるので、$f'(x)$は下記のように表せる。
$$
\large
\begin{align}
f'(x) = \frac{a}{2}x^{2} + bx + a
\end{align}
$$

$f'(x) = \frac{a}{2}x^{2}+bx+a$の両辺を$x$で積分すると下記が得られる。
$$
\large
\begin{align}
f(x) = \frac{a}{6}x^{3} + \frac{b}{2}x^{2} + ax + C_2
\end{align}
$$

ここで$f(0)=b$なので$C_2=b$が得られる。よって、$f(x)$は下記のように表せる。
$$
\large
\begin{align}
f(x) = \frac{a}{6}x^{3} + \frac{b}{2}x^{2} + ax + b
\end{align}
$$

上記より、$(3)$が正しい。

Q.15

$$
\large
\begin{align}
A+B &= \left(\begin{array}{cc} 2 & 2 \\ -3 & 3 \end{array} \right) \quad [1] \\
A-B &= \left(\begin{array}{cc} 4 & 2 \\ 1 & -3 \end{array} \right) \quad [2]
\end{align}
$$

$[1]+[2]$より下記が得られる。
$$
\large
\begin{align}
(A+B) + (A-B) &= \left(\begin{array}{cc} 2 & 2 \\ -3 & 3 \end{array} \right) + \left(\begin{array}{cc} 4 & 2 \\ 1 & -3 \end{array} \right) \\
2A &= \left(\begin{array}{cc} 6 & 4 \\ -2 & 0 \end{array} \right) \\
A &= \left(\begin{array}{cc} 3 & 2 \\ -1 & 0 \end{array} \right)
\end{align}
$$

同様に$[1]-[2]$より下記が得られる。
$$
\large
\begin{align}
(A+B) – (A-B) &= \left(\begin{array}{cc} 2 & 2 \\ -3 & 3 \end{array} \right) – \left(\begin{array}{cc} 4 & 2 \\ 1 & -3 \end{array} \right) \\
2B &= \left(\begin{array}{cc} -2 & 0 \\ -4 & 6 \end{array} \right) \\
B &= \left(\begin{array}{cc} -1 & 0 \\ -2 & 3 \end{array} \right)
\end{align}
$$

よって行列の積$AB$は下記のように得られる。
$$
\large
\begin{align}
AB &= \left(\begin{array}{cc} 3 & 2 \\ -1 & 0 \end{array} \right) \left(\begin{array}{cc} -1 & 0 \\ -2 & 3 \end{array} \right) \\
&= \left(\begin{array}{cc} -7 & 6 \\ 1 & 0 \end{array} \right)
\end{align}
$$

上記より$(2)$が正しい。

Q.16

$$
\large
\begin{align}
A = \left(\begin{array}{ccc} 0 & 1-i & 1 \\ 1+i & 0 & 1-i \\ 1 & 1+i & 0 \end{array} \right)
\end{align}
$$

上記に対し、固有多項式$F_{A}(\lambda)=\det{(\lambda I_{3}-A)}$は下記のように計算できる。
$$
\large
\begin{align}
F_{A}(\lambda) &= \det{(\lambda I_{3}-A)} = \left| \begin{array}{ccc} -\lambda & 1-i & 1 \\ 1+i & -\lambda & 1-i \\ 1 & 1+i & -\lambda \end{array} \right| \\
&= -\lambda^{3} + (1+i)^{2} + (1-i)^{2} – \left[ -\lambda – 2 \lambda(1+i)(1-i) \right] \\
&= -\lambda^{3} + 1+i^2+\cancel{2i} + 1+i^2-\cancel{2i} + \lambda + 2 \lambda(1-i^2) \\
&= -\lambda^{3} + \cancel{1}-\cancel{1}+ + \cancel{1}-\cancel{1} + \lambda + 2 \lambda \cdot (1+1) \\
&= -\lambda^{3} + 5 \lambda
\end{align}
$$

よって、固有方程式$F_{A}(\lambda)=\det{(\lambda I_{3}-A)}=0$は下記のように解ける。
$$
\large
\begin{align}
F_{A}(\lambda) = -\lambda^{3} + 5 \lambda &= 0 \\
\lambda(\lambda^2-5) &= 0 \\
\lambda &= 0, \, \pm \sqrt{5}
\end{align}
$$

ここで$\lambda_{1}<\lambda_{2}<\lambda_{3}$であるので、$\lambda_{1}=-\sqrt{5}, \, \lambda_{2}=0, \, \lambda_{3}=\sqrt{5}$である。よって$\displaystyle \frac{\lambda_{1}}{2} + \frac{\lambda_{2}}{3} + \frac{\lambda_{3}}{4}$は下記のように計算することができる。
$$
\large
\begin{align}
\frac{\lambda_{1}}{2} + \frac{\lambda_{2}}{3} + \frac{\lambda_{3}}{4} &= -\frac{\sqrt{5}}{2} + \frac{\sqrt{5}}{4} \\
&= -\frac{\sqrt{5}}{4}
\end{align}
$$

したがって$(5)$が正しい。

・解説
$3$次以上の正方行列の行列式の計算にあたっては余因子展開を用いることが多い一方で、この問題では余因子展開を用いると$i$の取り扱いにあたって式が複雑になります。一般に$n$次の正方行列の行列式の計算にあたって出てくる項の数は$n!$個であるので、$3$次の場合はうまく使い分けると良いです。

n次正方行列の行列式(determinants)の定義・計算とその解釈

余因子展開(cofactor expansion)の概要とその使用例の確認

Q.17

$$
\large
\begin{align}
X = \left(\begin{array}{cc} x & y \\ z & u \end{array} \right)
\end{align}
$$

上記のように$X$を表すと、$AX=XA$は下記のように表すことができる。
$$
\large
\begin{align}
AX &= XA \\
\left(\begin{array}{cc} a & b \\ c & d \end{array} \right) \left(\begin{array}{cc} x & y \\ z & u \end{array} \right) &= \left(\begin{array}{cc} x & y \\ z & u \end{array} \right) \left(\begin{array}{cc} a & b \\ c & d \end{array} \right) \\
\left(\begin{array}{cc} ax+bz & ay+by \\ cx+dz & cy+du \end{array} \right) &= \left(\begin{array}{cc} ax+cy & bx+dy \\ az+cu & bz+du \end{array} \right) \quad [1]
\end{align}
$$

$[1]$式より下記の連立方程式が得られる。
$$
\large
\begin{align}
\cancel{ax}+bz &= \cancel{ax}+cy \quad [2] \\
ay+by &= bx+dy \quad [3] \\
cx+dz &= az+cu \quad [4] \\
cy+\cancel{du} &= bz+\cancel{du} \quad [5]
\end{align}
$$

ここで$[2], [5]$式より、$bz=cy$が得られるが、この式が任意の$y,z$で成立する必要十分条件は$b=c=0$である。また、$b=c=0$を$[3], [4]$式に代入すると$a=d$が得られる。したがって$(4)$が正しい。

・解説
$a=d, \, b=c=0$は行列$A$が単位行列の定数倍を表すことも合わせて抑えておくと良いです。

Q.18

下記のように極限値を得ることができる。
$$
\large
\begin{align}
\lim_{x \to 0} \frac{\sin{bx}}{\sin{ax}} &= \lim_{x \to 0} \frac{\sin{bx}}{bx} \cdot \frac{ax}{\sin{ax}} \cdot \frac{b}{a} \\
&= 1 \cdot 1 \cdot \frac{b}{a} \\
&= \frac{b}{a}
\end{align}
$$

よって$(3)$が正しい。

・解説
この問題では$\displaystyle \lim_{\theta \to 0} \frac{\sin{\theta}}{\theta}=1$を用いました。$\displaystyle \lim_{\theta \to 0} \frac{\sin{\theta}}{\theta}=1$の導出は下記で取り扱ったので合わせて確認しておくと良いです。

三角関数の加法定理・倍角の公式・極限、微分の公式の簡易的な導出とその直感的理解

Q.19

$$
\large
\begin{align}
f(x,y) = \tan^{1}{(ax+by+1)}, \quad a \neq 0, \, b \neq 0
\end{align}
$$

$2$変数関数$f(x,y)$のマクローリン展開は下記のように表せる。
$$
\begin{align}
f(x,y) = f(0,0) + \frac{1}{1!} \left( x \frac{\partial}{\partial x} + y \frac{\partial}{\partial y} \middle) f(x,y) \right|_{x=0,y=0} + \frac{1}{2!} \left( x \frac{\partial}{\partial x} + y \frac{\partial}{\partial y} \middle)^{2} f(x,y) \right|_{x=0,y=0} + \cdots
\end{align}
$$

上記より$xy$の係数は$\displaystyle \frac{\partial^{2}}{\partial x \partial y} f(x,y) \Bigr|_{x=0,y=0}$を計算することで得られる。ここで$\displaystyle (\tan^{-1}{x})’ = \frac{1}{1+x^2}$であるので、$xy$の係数は下記のように得られる。
$$
\large
\begin{align}
\frac{\partial^{2}}{\partial x \partial y} f(x,y) \Bigr|_{x=0,y=0} &= \frac{-2ab(ax+by+1)}{[1+(ax+by+1)]^{2}} \Bigr|_{x=0,y=0} \\
&= \frac{-2ab \cdot (0+0+1)}{[1+(0+0+1)]^{2}} \\
&= -\frac{2ab}{4} = -\frac{ab}{2}
\end{align}
$$

・解説
$\displaystyle (\tan^{-1}{x})’ = \frac{1}{1+x^2}$の導出は下記で取り扱いました。

逆三角関数(inverse trigonometric function)の微分の公式の導出

Q.20

$$
\large
\begin{align}
2020 \times \frac{\displaystyle \int_{0}^{1} (1-x^{20})^{100} dx}{\displaystyle \int_{0}^{1} (1-x^{20})^{101} dx} \quad [1]
\end{align}
$$

$\displaystyle I_{n} = \int_{0}^{1} (1-x^{20})^{n} dx, \, n \geq 1$とおくと、部分積分法により下記のように漸化式が得られる。
$$
\large
\begin{align}
I_{n} &= \int_{0}^{1} (1-x^{20})^{n} dx \\
&= \left[ x(1-x^{20})^{n} \right]_{0}^{1} – \int_{0}^{1} x \cdot n(1-x^{20})^{n-1} \cdot (-20x^{19}) dx \\
&= 20n \int_{0}^{1} x^{20}(1-x^{20})^{n-1} dx \\
&= 20n \int_{0}^{1} (1-x^{20})^{n-1} dx – 20n \int_{0}^{1} (1-x^{20}) (1-x^{20})^{n-1} dx \\
&= 20n \int_{0}^{1} (1-x^{20})^{n-1} dx – 20n \int_{0}^{1} (1-x^{20})^{n} dx \\
&= 20n I_{n-1} – 20n I_{n} \\
(20n+1) I_{n} &= 20n I_{n-1} \\
I_{n} &= \frac{20n}{20n+1} I_{n-1} \quad [2]
\end{align}
$$

$[2]$式に$n=101$を代入すると下記が得られる。
$$
\large
\begin{align}
I_{101} &= \frac{20 \cdot 101}{20 \cdot 101 + 1} I_{101-1} \quad [2]’ \\
I_{101} &= \frac{2020}{2021} I_{100} \quad [3]
\end{align}
$$

$[3]$式より、$[1]$式は下記のように計算できる。
$$
\large
\begin{align}
2020 \times \frac{\displaystyle \int_{0}^{1} (1-x^{20})^{100} dx}{\displaystyle \int_{0}^{1} (1-x^{20})^{101} dx} &= 2020 \times \frac{I_{100}}{I_{101}} \\
&= 2020 \cdot I_{100} \cdot \frac{2021}{2020 I_{100}} \\
&= 2021
\end{align}
$$

上記より$(5)$が正しい。

「データサイエンス 数学ストラテジスト 上級」はデータサイエンスの基盤である、確率・統計、線形代数、微積分、機械学習、プログラミングなどを取り扱う資格試験です。当記事では「日本数学検定協会」作成の「公式問題集」の演習問題$1$〜$10$の解答例を取り扱いました。

・数学検定まとめ
https://www.hello-statisticians.com/math_certificate

演習問題

Q.1

$$
\large
\begin{align}
x^{2} + \frac{1}{x^2} = 10
\end{align}
$$

上記の式は下記のように変形できる。
$$
\large
\begin{align}
x^{2} + \frac{1}{x^2} &= 10 \\
\left( x + \frac{1}{x} \right)^{2} – 2 &= 10 \\
\left( x + \frac{1}{x} \right)^{2} &= 12
\end{align}
$$

ここで$x>1$より、$\displaystyle x + \frac{1}{x} = 2 \sqrt{3}$が成立するが、下記のように変形を行える。
$$
\large
\begin{align}
x + \frac{1}{x} &= 2 \sqrt{3} \\
x^{2} – 2 \sqrt{3} x + 1 &= 0 \\
x &= \sqrt{3} \pm \sqrt{3-1} = \sqrt{3} \pm \sqrt{2}
\end{align}
$$

$x>1$なので$x=\sqrt{2}+\sqrt{3}$が成立する。

・解説
$x>1$を元に$\pm$を外す際に注意が必要です。$\displaystyle x + \frac{1}{x} > 1$や$\sqrt{3}-\sqrt{2}<1$を途中計算で用いました。

Q.2

$n$角形の$1$つの点に対し、線分が対角線である点は$n-3$、辺である点は$2$つ存在する。ここで$n-3=2$であれば$p=q$である。よって$n=5$であれば良い。

・解説
問題集の解答では$2$点選ぶことを${}_{n} C_{2}$で表現されますが、このように表すと式がやや複雑です。$1$点はどの点を選んでも他の点に関する取り扱いは同じであることに着目することで計算を簡略化することが可能です。

Q.3

$$
\large
\begin{align}
y &= \log_{2}{\frac{1}{x}} \\
&= \log_{2}{x^{-1}} \\
&= -\log_{2}{x}
\end{align}
$$

上記より$(3)$のグラフが正しい。

Q.4

$$
\large
\begin{align}
\sqrt{10}x^2 – 2x + k = 0
\end{align}
$$

上記の方程式の解が$\sin{\theta}, \, \cos{\theta}$であるとき、二次方程式の解と係数の関係より下記が成立する。
$$
\large
\begin{align}
\sin{\theta} + \cos{\theta} &= \frac{2}{\sqrt{10}} \quad [1] \\
\sin{\theta} \cos{\theta} &= \frac{k}{\sqrt{10}} \quad [2]
\end{align}
$$

ここで$(1)$式の両辺の$2$乗は下記のように変形できる。
$$
\large
\begin{align}
(\sin{\theta} + \cos{\theta})^{2} &= \frac{2^2}{\sqrt{10}^2} \quad [1]’ \\
\sin^{2}{\theta} + \cos^{2}{\theta} + 2 \sin{\theta} \cos{\theta} &= \frac{2}{5} \\
1 + 2 \sin{\theta} \cos{\theta} &= \frac{2}{5} \\
2 \sin{\theta} \cos{\theta} &= -\frac{3}{5} \\
\sin{\theta} \cos{\theta} &= -\frac{3}{10} \quad [3]
\end{align}
$$

$[2], \, [3]$式より下記のように$k$の値が得られる。
$$
\large
\begin{align}
\frac{k}{\sqrt{10}} &= -\frac{3}{10} \\
k &= -\frac{3}{\sqrt{10}}
\end{align}
$$

上記より、元の二次方程式は下記のように表せる。
$$
\large
\begin{align}
\sqrt{10}x^2 – 2x + -\frac{3}{\sqrt{10}} &= 0 \\
10x^2 – 2 \sqrt{10} x + -3 &= 0
\end{align}
$$

二次方程式の解の公式より、上記の方程式の解は下記のように得られる。
$$
\large
\begin{align}
x &= \frac{\sqrt{10} \pm \sqrt{\sqrt{10}^{2} + 10 \cdot 3}}{10} \\
&= \frac{\sqrt{10} \pm 2 \sqrt{10}}{10} \\
&= -\frac{\sqrt{10}}{10}, \, \frac{3 \sqrt{10}}{10}
\end{align}
$$

上記より$(1)$が正しい。

Q.5

$$
\large
\begin{align}
\left( \frac{2}{x} \right)^{\log_{e}{2}} &= \left( \frac{3}{y} \right)^{\log_{e}{3}} \quad [1] \\
3^{-\log_{e}{x}} &= 2^{-\log_{e}{y}} \quad [2]
\end{align}
$$

上記に対し、$\displaystyle X=\frac{1}{x}, \, Y=\frac{1}{y}$のようにおくと、$[1], \, [2]$式は下記のように表せる。
$$
\large
\begin{align}
(2X)^{\log_{e}{2}} &= (3Y)^{\log_{e}{3}} \quad [1]’ \\
3^{\log_{e}{X}} &= 2^{\log_{e}{Y}} \quad [2]’
\end{align}
$$

上記の$[1]’$式の両辺の自然対数を取ると、下記が得られる。
$$
\large
\begin{align}
(2X)^{\log_{e}{2}} &= (3Y)^{\log_{e}{3}} \quad [1]’ \\
\log_{e}{2} \log_{e}{(2X)} &= \log_{e}{3} \log_{e}{(3Y)} \\
\log_{e}{2} (\log_{e}{2} + \log_{e}{X}) &= \log_{e}{3} (\log_{e}{3} + \log_{e}{Y}) \quad [1]^{”}
\end{align}
$$

同様に$[2]’$式の両辺の自然対数を取ると、下記が得られる。
$$
\large
\begin{align}
3^{\log_{e}{X}} &= 2^{\log_{e}{Y}} \quad [2]’ \\
\log_{e}{X} \log_{e}{3} &= \log_{e}{Y} \log_{e}{2} \\
\log_{e}{Y} &= \frac{\log_{e}{3}}{\log_{e}{2}} \log_{e}{X} \quad [2]^{”}
\end{align}
$$

ここで$[2]^{”}$式を$[1]^{”}$式に代入することで下記のように変形できる。
$$
\large
\begin{align}
\log_{e}{2} (\log_{e}{2} + \log_{e}{X}) &= \log_{e}{3} (\log_{e}{3} + \log_{e}{Y}) \quad [1]^{”} \\
\log_{e}{2} (\log_{e}{2} + \log_{e}{X}) &= \log_{e}{3} \left( \log_{e}{3} + \frac{\log_{e}{3}}{\log_{e}{2}} \log_{e}{X} \right) \\
\frac{1}{\log_{e}{2}} \cancel{\left( (\log_{e}{2})^{2} – (\log_{e}{3})^{2} \right)} \log_{e}{X} &= -\cancel{\left( (\log_{e}{2})^{2} – (\log_{e}{3})^{2} \right)} \\
\log_{e}{X} &= -\log_{e}{2} \\
\log_{e}{X} &= \log_{e}{2^{-1}} \\
X &= \frac{1}{2}
\end{align}
$$

上記を$[2]^{”}$式に代入することで下記が得られる。
$$
\large
\begin{align}
\log_{e}{Y} &= \frac{\log_{e}{3}}{\log_{e}{2}} \log_{e}{X} \quad (2)^{”} \\
\log_{e}{Y} &= \frac{\log_{e}{3}}{\log_{e}{2}} \cdot -\log_{e}{2} \\
\log_{e}{Y} &= -\log_{e}{3} \\
\log_{e}{Y} &= \log_{e}{3^{-1}} \\
Y &= \frac{1}{3}
\end{align}
$$

ここで$\displaystyle X=\frac{1}{x}, \, Y=\frac{1}{y}$であるので、$x=2, y=3$である。よって$x^2+y^2=13$であるので$(1)$が正しい。

Q.6

$$
\large
\begin{align}
f(x) = x|x-3|
\end{align}
$$

上記より、$x<3$のとき$f(x)=-x(x-3)=-x^2+3x, \, f'(x)=-2x+3$、$3 \leq x$のとき$f(x)=x(x-3)=x^2-3x, \, f'(x)=2x-3$である。よって$f'(2)-f'(4)$は下記のように計算できる。
$$
\large
\begin{align}
f'(2) – f'(4) &= (-2 \cdot 2 + 3) – (2 \cdot 4 – 3) \\
&= -1 – 5 \\
&= -6
\end{align}
$$

上記より$(1)$が正しい。

Q.7

$$
\large
\begin{align}
f(x) = \int_{-1}^{x} (t^2-t-2) dt
\end{align}
$$

$g(t)=t^2-t-2$の原始関数を$G(t)$とおくと、$f'(x)$は下記のように得ることができる。
$$
\large
\begin{align}
f'(x) &= \frac{d}{dx} \int_{-1}^{x} g(t) dt \\
&= \frac{d}{dx} (G(x)-G(-1)) \\
&= g(x) \\
&= x^2 – x – 2 \\
&= (x+1)(x-2)
\end{align}
$$

上記より、関数$f(x)$は$x=-1$で極大値$M$、$x=2$で極小値$m$を取る。$M$と$m$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
M &= f(-1) = \int_{-1}^{-1} (t^2-t-2) dt \\
&= 0 \\
m &= f(2) = \int_{-1}^{2} (t^2-t-2) dt \\
&= \left[ \frac{1}{3}t^{3} – \frac{1}{2}t^{2} – 2t \right]_{-1}^{2} \\
&= \left( \frac{8}{3} – 2 – 4 \right) – \left( -\frac{1}{3} – \frac{1}{2} + 2 \right) \\
&= \frac{16-36+2+3-12}{6} \\
&= -\frac{27}{6} \\
&= -\frac{9}{2}
\end{align}
$$

上記より$(4)$が正しい。

Q.8

$\displaystyle X \sim \mathrm{Bin} \left( 90, \frac{1}{3} \right)$であるので、期待値$E[X]$と標準偏差$SD[X]=\sqrt{V[X]}$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
E[X] &= 90 \times \frac{1}{3} \\
&= 30 \\
SD[X] &= \sqrt{V[X]} \\
&= \sqrt{90 \times \frac{1}{3} \times \frac{2}{3}} \\
&= \sqrt{20} = 2 \sqrt{5}
\end{align}
$$

上記より、$(5)$が正しい。

Q.9

$$
\large
\begin{align}
I_{A} &= -\log_{2}{p_{A}} \\
p_{A} &= \frac{2}{10} \times \frac{1}{9} \\
&= \frac{1}{45}
\end{align}
$$

上記より選択情報量$I_{A}$は下記のように計算できる。
$$
\large
\begin{align}
I_{A} &= -\log_{2}{\frac{1}{45}} \\
&= \log_{2}{(3^{2} \times 5)} \\
&= 2 \log_{2}{3} + \log_{2}{5} \\
&= 2 \times 1.585 + 2.322 \\
&= 5.492
\end{align}
$$

よって$(3)$が正しい。

Q.10

$$
\large
\begin{align}
\vec{a} = \left(\begin{array}{c} 3 \\ -2 \\ 1 \end{array} \right), \quad \vec{b} = \left(\begin{array}{c} -6 \\ k \\ -2 \end{array} \right)
\end{align}
$$

$\vec{a}$と$\vec{b}$が平行のとき、$-2\vec{a} = \vec{b}$が成立する必要がある。このとき$k=4$である。逆に$k=4$のとき$\vec{a}$と$\vec{b}$が平行であるので、$k_1=4$が必要十分である。

$\vec{a} \perp \vec{b}$のとき、$\vec{a} \cdot \vec{b} = 0$より下記が成立する。
$$
\large
\begin{align}
\vec{a} \cdot \vec{b} &= 0 \\
-18 – 2k -2 &= 0 \\
k &= -10
\end{align}
$$

よって$k_2=-10$である。したがって$(3)$が正しい。