n次正方行列の行列式(determinants)の定義・計算とその解釈

行列式(determinants)は多次元正規分布の定数項や多次元分布の確率密度関数の変数変換の際のヤコビアンの計算など、統計学を学ぶ上でも重要な概念です。当記事では行列式に関し、定義や定義から導出される公式、また行列式の解釈について取りまとめを行いました。

作成にあたってはWikipediaの行列式のページや、「統計のための行列代数(Matrix Algebra From a Statistician’s Perspective)」のCh.$13$や「パターン認識と機械学習」のAppendix.Cを参考に作成を行いました。

行列式の定義と具体例

行列式の定義

$n \times n$正方行列$A = (a_{ij})$の行列式を$\det{A}$のように表すとき、$\det{A}=|A|$は下記のように定義される。
$$
\large
\begin{align}
\det{A} = |A| = \sum_{\sigma \in \mathrm{Aut}(n)} \left[ \mathrm{sgn} (\sigma) \prod_{i=1}^{n} a_{i,\sigma(i)} \right]
\end{align}
$$

上記の式を理解するにあたってはまず$\sigma$を抑えると良い。ここで$\sigma(i)$は$i=1,…,n$に対応して$1,…,n$の値を並べ替えたものが対応する。たとえば、$i=1,2,3$のとき$\sigma(1)=2,\sigma(2)=3,\sigma(3)=1$が一例である。

このように$\sigma$を定義することで、「それぞれの行と列から$1$つずつ選んだ$n$個の数」を選び出すことができる。文面だけだとわかりにくいので、以下のように$3 \times 3$行列でいくつか図示を行なった。

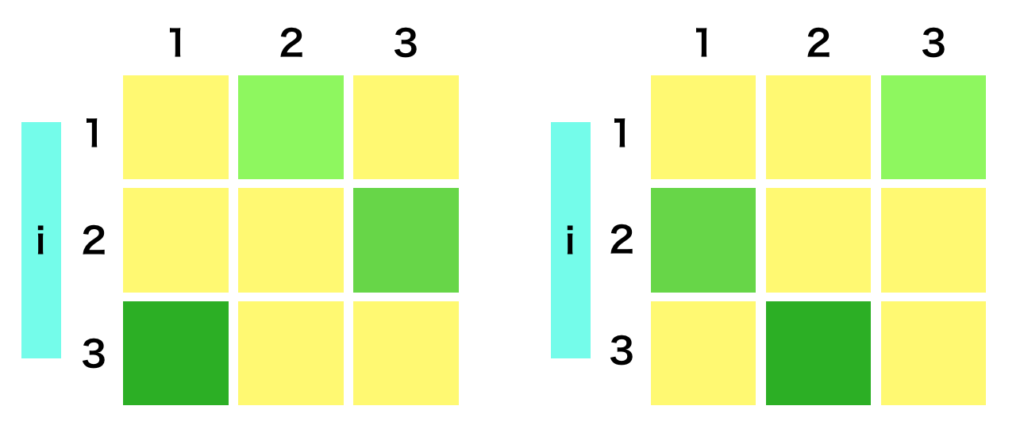
上の図では$\sigma(1)=2,\sigma(2)=3,\sigma(3)=1$と$\sigma(1)=3,\sigma(2)=1,\sigma(3)=2$を元に行列$A = (a_{i,\sigma(i)})$の図示を行なった。緑の薄い順に各要素を選んだことが図より確認でき、どの行と列に着目しても緑の要素が$1$つずつ抽出されていることが確認できる。

行列式では上記のような手続きで抽出された行列$A$の要素$a_{i,\sigma(i)}$に対し積を計算し、$\mathrm{sgn}(\sigma)$をかけ、全ての考えられうる$\sigma$に対して和を計算する。ここで全ての考えられうる$\sigma$は$\sigma \in \mathrm{Aut}(n)$のように表現されているが、$n!$通りの並べ方を考慮すると理解すればよい。$n=3$の場合を例に考えると、$\sigma$は「$1,2,3$」、「$1,3,2$」、「$2,1,3$」、「$2,3,1$」、「$3,1,2$」、「$3,2,1$」の$6$通り考えることができる。

また、$\mathrm{sgn}(\sigma)$は$i<j$に対して$\sigma(i)>\sigma(j)$となる要素の組の数を$\phi_{\sigma}$とおくとき$\mathrm{sgn} (\sigma) = (-1)^{\phi_{\sigma}}$に対応する。

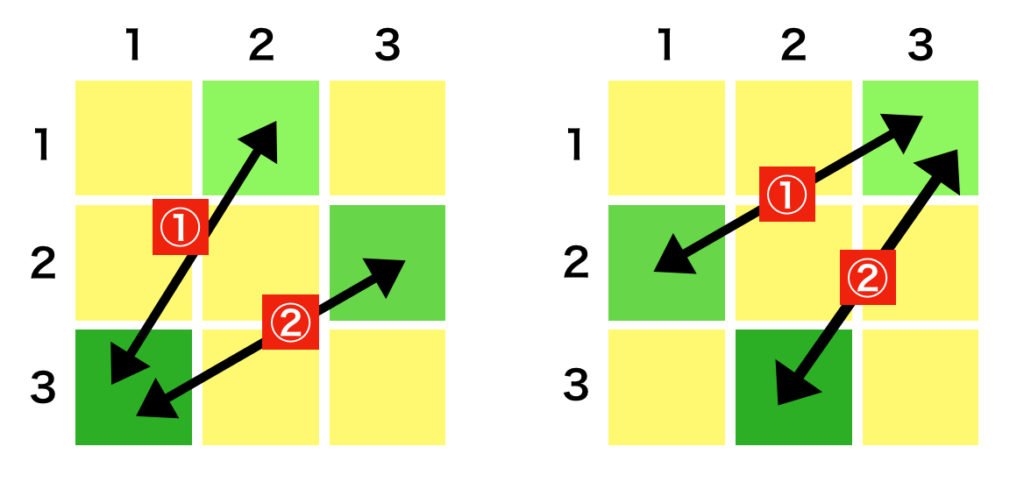
$\mathrm{sgn} (\sigma) = (-1)^{\phi_{\sigma}}$に関しては上記のように図示を行うことができる。

ここまでは$n \times n$正方行列に基づいて定義の確認を行なったが、以下具体的に確認するにあたって、$2 \times 2$や$3 \times 3$行列に関して確認を行う。

$2 \times 2$行列の行列式

$$
\large
\begin{align}
A = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right)
\end{align}
$$

前項で取り扱った式を上記の$2 \times 2$正方行列に当てはめることを考える。$1,2$の並び替えは「$1,2$」と「$2,1$」が考えられることから、対応する行列式$\det{A}$は下記のように計算することができる。
$$
\large
\begin{align}
\det{A} &= |A| = \left| \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| = \sum_{\sigma \in \mathrm{Aut}(2)} \left[ \mathrm{sgn} (\sigma) \prod_{i=1}^{2} a_{i,\sigma(i)} \right] \\
&= (-1)^{0} a_{11} a_{22} + (-1)^{1} a_{12} a_{21} \\
&= a_{11} a_{22} – a_{12} a_{21}
\end{align}
$$

$3 \times 3$行列の行列式

$$
\large
\begin{align}
A = \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right)
\end{align}
$$

$n \times n$行列の行列式の定義を上記の$3 \times 3$正方行列に当てはめることを考える。$1,2,3$の並び替えは「$1,2,3$」、「$1,3,2$」、「$2,1,3$」、「$2,3,1$」、「$3,1,2$」、「$3,2,1$」が考えられることから、対応する行列式$\det{A}$は下記のように計算することができる。
$$
\large
\begin{align}
& \det{A} = |A| = \sum_{\sigma \in \mathrm{Aut}(3)} \left[ \mathrm{sgn} (\sigma) \prod_{i=1}^{3} a_{i,\sigma(i)} \right] \\
&= (-1)^{0} a_{11} a_{22} a_{33} + (-1)^{1} a_{11} a_{23} a_{32} + (-1)^{1} a_{12} a_{21} a_{33} + (-1)^{2} a_{12} a_{23} a_{31} + (-1)^{2} a_{13} a_{21} a_{32} + (-1)^{3} a_{13} a_{22} a_{33} \\
&= a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} – a_{11} a_{23} a_{32} – a_{12} a_{21} a_{33} – a_{13} a_{22} a_{33}
\end{align}
$$

$(-1)$の累乗の数はそれぞれ下記に対応すると考えることができる。

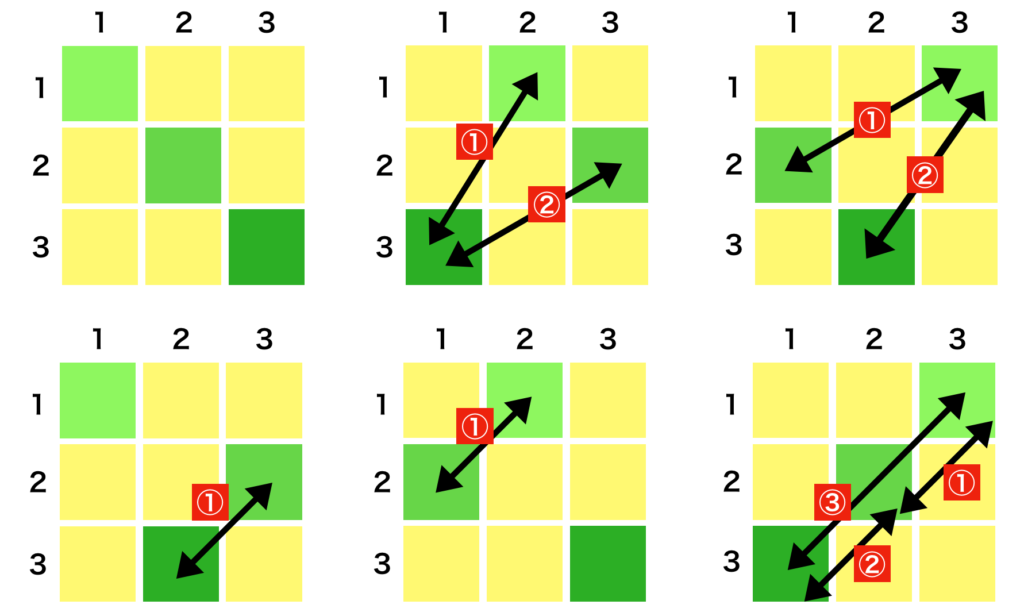
行列式の解釈

平行四辺形の面積

$$
\large
\begin{align}
A = \left(\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right)
\end{align}
$$
下記で詳しく取り扱ったが、上記の$2 \times 2$行列の行列式は$4$点$(0,0), (a_{11},a_{12}), (a_{11}+a_{21},a_{12}+a_{22}), (a_{21},a_{22})$で構成される平行四辺形の面積に一致する。
https://www.hello-statisticians.com/explain-terms-cat/transformation1.html

行列式に関する公式

「パターン認識と機械学習」を参考に行列式に関して抑えておくと良い公式を以下にまとめる。対応がわかりやすいように$(o.xx)$の形式の数式の番号は「パターン認識と機械学習」のものを用いた。

$|AB| = |A||B|$

$$
\large
\begin{align}
|AB| = |A||B| \quad (C.12)
\end{align}
$$

導出は複雑なので詳しくは下記で取り扱った。
https://www.hello-statisticians.com/explain-terms-cat/matrix_determinants2.html

$\displaystyle |A^{-1}| = \frac{1}{|A|}$

$AA^{-1} = A^{-1}A = I$に$(C.12)$式を用いることで下記が導出できる。
$$
\large
\begin{align}
|A^{-1}A| &= |A^{-1}||A| = |I| \quad (C.12)’ \\
|A^{-1}||A| &= 1 \\
|A^{-1}| &= \frac{1}{|A|} \quad (C.13)
\end{align}
$$

$\displaystyle |A| = \prod_{i=1}^{M} \lambda_{i}$

$A$を固有ベクトルに基づいて列を構成する直交行列$U$と、固有値$\lambda_{i}$を対角に並べた対角行列$\Lambda$を用いて下記のように固有値分解を行うことを考える。
$$
\large
\begin{align}
A = U \Lambda U^{\mathrm{T}}
\end{align}
$$

上記の式に$(C.12)$式を用いることで下記が導出できる。
$$
\large
\begin{align}
|A| &= |U \Lambda U^{\mathrm{T}}| \\
&= |U| |\Lambda| |U^{\mathrm{T}}| \\
&= |\Lambda| = \prod_{i=1}^{M} \lambda_{i} \quad (C.47)
\end{align}
$$

参考

・行列式 Wikipedia
・平行四辺形の面積の計算とヤコビ行列式
https://www.hello-statisticians.com/explain-terms-cat/transformation1.html