PPO(Proximal Policy Optimization)まとめ

方策勾配法の学習の安定化にあたっては、TRPO(Trust Region Policy Optimization)やPPO(Proximal Policy Optimization)のようにステップ幅の調整が解決策になります。当記事ではPPOについて詳しく取りまとめを行いました。
「ゼロから作るDeep Learning④ー強化学習編」の$10.2.3$の「TRPO・PPO」やTRPO、PPOの論文などを参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

・TRPO論文
・PPO論文

ゼロから作るDeep Learning ❹ ―強化学習編

斎藤 康毅

3,960円(04/29 17:41時点)

Amazon

前提の確認

方策勾配法まとめ

方策勾配法の目的関数や勾配

軌道$\tau$の収益$G(\tau)$を最大にするような方策$\pi_{\theta}(A_t|S_t)$を得るにあたっては、下記の目的関数を$p$次元ベクトル$\theta$について最大化すればよい。
$$
\large
\begin{align}
J(\theta) &= \mathbb{E}_{\tau \sim \pi_{\theta}}[G(\tau)] \quad (1.1) \\
\theta & \in \mathbb{R}^{p}
\end{align}
$$

上記で定義した$J(\theta)$の勾配ベクトルは下記のように表される。
$$
\large
\begin{align}
\nabla_{\theta} J(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta}} \left[ \sum_{t=0}^{T} G(\tau) \nabla_{\theta} \log{\pi_{\theta}(A_t|S_t)} \right] \quad (1.2)
\end{align}
$$

詳しい導出は下記で取り扱った。

REINFORCEMENT、ベースライン、Actor-Critic

$(1.1)$式では収益$G(\tau)$を元に目的関数$J(\theta)$を定義し、勾配ベクトル$\nabla_{\theta} J(\theta)$を$(1.2)$式で表した。$(1.2)$式は収益$G(\tau)$に基づいて軌道の重み付けを行なったと大まかに解釈できるが、本来的には状態$S_t$後の収益のみを用いるのがより適切である。このように$(1.2)$式の$G(\tau)$については様々な表し方が考えられるので、$(1.2)$式を$G(\tau)$を一般化した$\Phi_{t}$を用いて下記のように再定義する。
$$
\large
\begin{align}
\nabla_{\theta} J(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta}} \left[ \sum_{t=0}^{T} \Phi_{t} \nabla_{\theta} \log{\pi_{\theta}(A_t|S_t)} \right] \quad (1.3)
\end{align}
$$

上記の一例であるベースライン付きREINFORCEは、$\Phi_{t}$を下記のように定義する。
$$
\large
\begin{align}
\Phi_{t} &= G_{t} – b(S_t) \quad (1.4) \\
G_t &= R_t + \gamma R_{t+1} + \gamma^{2} R_{t+2} + \cdots + \gamma^{T-t} R_{T} \quad (1.5)
\end{align}
$$

ここで上記の収益$G_t$にQ関数$Q(S_t,A_t)$、ベースライン$b(S_t)$に価値関数を用いると$\Phi_{t}$はアドバンテージ関数$A(S_t,A_t)$に一致する。
$$
\large
\begin{align}
\Phi_{t} &= Q(S_t,A_t) – V(S_t) \\
&= A(S_t,A_t) \quad (1.6)
\end{align}
$$

アドバンテージ関数は状態$S_t$における行動$A_t$の評価を単体で行うことができるように定義される関数である。また、オーソドックスなREINFORCEやActor-Criticなどベースライン付きREINFORCE以外の$\Phi_{t}$の定義は下記で詳しく取りまとめた。

TRPO

TRPOの最適化問題は下記のように表される。
$$
\large
\begin{align}
\mathrm{maximize}_{\theta} &: \, \mathbb{E}_{t} \left[ \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t|s_t)} A_{t} \right] \quad (1.7) \\
\mathrm{subject \, to} &: \, \mathbb{E}_{t} \left[ KL[\pi_{\theta_{\mathrm{old}}}(\cdot|s_t),\pi_{\theta}(\cdot|s_t)] \right] \leq \delta \quad (1.8) \\
\theta & \in \mathbb{R}^{p}, \, \theta_{\mathrm{old}} \in \mathbb{R}^{p}
\end{align}
$$

$(1.7)$式を$(1.8)$式の制約を元に最適化するにあたって、TRPOでは共役勾配法と直線探索を用いる。詳細は下記で取り扱った。

$(1.8)$式の制約により、繰り返し演算における変化の幅の上限値を設定することが可能で学習の安定化が実現できる一方で、計算コストがやや大きい。PPOはこの計算コストを解決した手法である。

PPO

PPOの目的関数と学習の流れ

Clipped Surrogate Objective

TRPOにおける目的関数(Objective function)を”conservative policy iteration”に基づいて$L^{CPI}(\theta)$とおくと、$L^{CPI}(\theta)$は確率の比率である$r_{t}(\theta)$を用いて、下記のように表すこともできる。
$$
\large
\begin{align}
L^{CPI}(\theta) &= \mathbb{E}_{t} \left[ \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t|s_t)} A_{t} \right] = \mathbb{E}_{t} \left[ r_{t}(\theta) A_t \right] \quad (2.1) \\
r_{t}(\theta) &= \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t|s_t)} \quad (2.2)
\end{align}
$$

$(2.1)$式に対して、PPOでは下記のような目的関数の$L^{CPI}(\theta)$を用いる。
$$
\large
\begin{align}
L^{CLIP}(\theta) &= \mathbb{E}_{t} \left[ \min \left( r_{t}(\theta)A_t, \, \mathrm{clip}(r_{t}(\theta), 1-\varepsilon, 1+\varepsilon)A_t \right) \right] \quad (2.3)
\end{align}
$$

$(2.3)$式は$\min$の内側に下記の二つの項を持つ。
$$
\large
\begin{align}
& r_{t}(\theta)A_t \\
& \mathrm{clip}(r_{t}(\theta), 1-\varepsilon, 1+\varepsilon)A_t
\end{align}
$$

第$1$項を選ぶ場合、$(2.3)$式は$(2.1)$式に一致するので$L^{CLIP}(\theta)$は$L^{CPI}(\theta)$に一致する。

第$2$項は$r_{t}$の変化を$1-\varepsilon$以上$1+\varepsilon$以下に抑える関数である。第$2$項があることで、一度のパラメータのUpdateにおけるパラメータの変化が大きくなり過ぎないように制約を課すことができる。

$(2.3)$式は下記の図を元に理解すると良い。

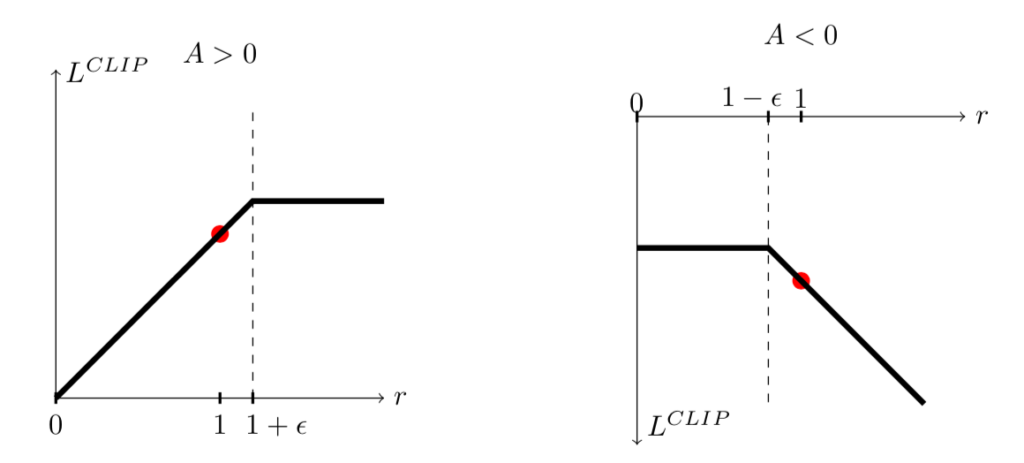
図の理解にあたっては、「$1-\varepsilon$と$1+\varepsilon$のどちらを用いるかはアドバンテージ関数$A_t$の符号による」ことに注意する必要がある。アドバンテージ関数が正であるときは$1+\varepsilon$を用い、負の場合は$1-\varepsilon$を用いる。

Adaptive KL Penalty Coefficient

PPO論文では目的関数$L^{CPI}(\theta)$(conservative policy iteration)に加えて、下記のような目的関数$L^{KLPEN}(\theta)$に基づいた実験の結果の記載がある。
$$
\large
\begin{align}
L^{KLPEN}(\theta) &= \mathbb{E}_{t} \left[ \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t|s_t)} A_{t} \, – \, \beta \mathrm{KL}\left[ \pi_{\theta_{\mathrm{old}}}(\cdot|s_t), \pi_{\theta}(\cdot|s_t) \right] \right] \quad (2.4) \\
d &= \mathbb{E}_{t} \left[ \mathrm{KL}\left[ \pi_{\theta_{\mathrm{old}}}(\cdot|s_t), \pi_{\theta}(\cdot|s_t) \right] \right] \quad (2.5)
\end{align}
$$

目的関数$L^{KLPEN}(\theta)$の”KLPEN”は”KL penalty”の略である。また、$\beta$の値は固定(fixed)する場合と、$(2.5)$式の$d$の値に基づいて適応的に(Adaptive)変化させる方法の二通りが取り扱われる。

適応的な手法を用いる場合はハイパーパラメータのd_targの値を元に、下記のようなプログラムに基づいて$\beta$の値を変化させる。

beta = 
d_targ = 

for i in range(n_epoch):
    d = calc_KL()
    if d < d_targ/1.5:
        beta = beta/2
    elif d > d_targ*1.5:
        beta = beta*2

上記の処理は$(2.5)$式に基づいて計算を行ったKLダイバージェンスの値が小さければペナルティの係数$\beta$を小さくし、KLダイバージェンスの値が大きければペナルティの係数$\beta$を大きくすることに対応する。よって、「確率分布の変動が大きい場合にペナルティを大きくする」と解釈することができる。また、betaの初期値もハイパーパラメータであるが、アルゴリズムがすぐに適応するので値は重要でないとPPO論文に記載がある。

PPOの学習の流れ

$(2.3), (2.4)$式の目的関数を元に、PPOの学習の流れは下記のように表される。

PPO論文における実験

PPO論文では下記の数式に基づいてそれぞれ実験が行われる。

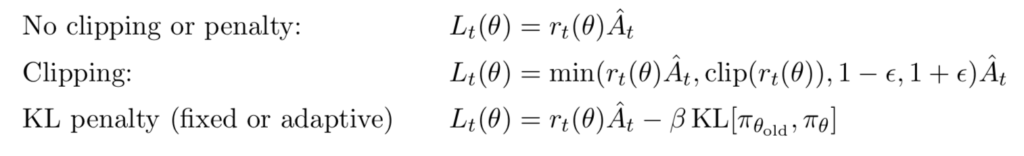
上記のClippingは「Clipped Surrogate Objective」、KL penaltyは「Adaptive KL Penalty Coefficient」で取り扱った内容にそれぞれ対応する。このそれぞれの目的関数を用いて、OpenAI Gymで実装されているHalfCheetah、Hopper、InvertedDoublePendulum、InvertedPendulum、Reacher、Swimmer、Walker2dの$7$つのsimulated robotic tasksについて学習を行った結果が下記である。

上記は$7$つのタスクのスコアの正規化された平均であり、$\epsilon=0.2$のClippingが最も良い結果であることが確認できる。また、Adaptive KLの$\beta$の初期値はここでは$\beta=1$に設定される。

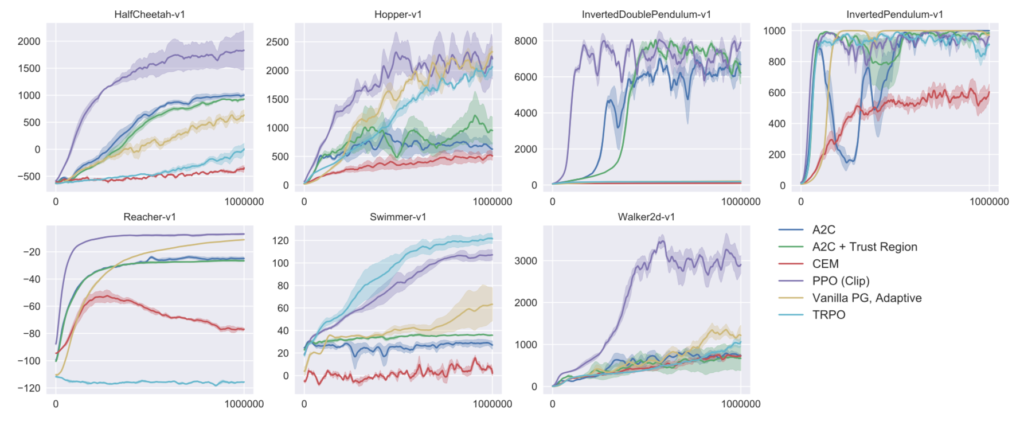
また、論文のFigure$3$ではPPOに加えてA$2$CやTRPOなど、その他アルゴリズムの学習の結果についてまとめられているので合わせて確認しておくと良い。紫がPPOであり、相対的に良い結果であることが確認できる。

・注意事項
PPO論文では「$\epsilon=0.2$のClipping」が最も良い結果とされるが、InstructGPT/ChatGPTでは「Clipped Surrogate Objective」ではなく、「Adaptive KL Penalty Coefficient」に基づく目的関数が用いられることに注意が必要である。