Routing TransformerのようなContent-based Sparse Attentionでは最大内積探索(MIPS; Maximum Inner Product Search)と類似した処理が行われます。当記事では最大内積探索の概要やクラスタリングを用いた計算の効率化について取りまとめました。
「Clustering is efficient for approximate maximum inner product search.」などを参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
最大内積探索の問題設定
最大内積探索の立式
$n$個の$D$次元ベクトルの集合$\mathcal{X}$を$\mathcal{X} = \{ \mathbf{x}_{1}, \cdots , \mathbf{x}_{n} \}, \, \mathbf{x}_{i} \in \mathbb{R}^{D}$のように定義する。このとき$D$次元のクエリ$q \in \mathbb{R}^{D}$と集合$\mathcal{X}$の要素であるベクトル$\mathbf{x}_{i}$に関する最大内積探索問題(MIPS; Maximum Inner Product Search problem)は下記のように立式することができる。
$$
\large
\begin{align}
\mathrm{arg} \max_{i} q^{\mathrm{T}} \mathbf{x}_{i}
\end{align}
$$
同様に、内積の計算結果が上位$K$に含まれるベクトルを探すK-MIPS問題は下記のように立式される。
$$
\large
\begin{align}
\mathrm{argmax}_{i}^{(K)} q^{\mathrm{T}} \mathbf{x}_{i} \quad (1.1)
\end{align}
$$
最近傍探索と一致する場合
最大内積探索(MIPS)問題は最近傍探索(NNS; Nearest Neighbor Search)と関連する。より厳密には「ベクトル$\mathbf{x}_{i} \in \mathbb{R}^{D}$が同じユークリッドノルム(Euclidean norm)を持つ場合」にMIPSとNNSが一致する。K-NNSの式はクエリ$q$とベクトル$\mathbf{x}_{i}$間のノルムに着目することで上記のように表すことができる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} ||q \, – \, \mathbf{x}_{i}||^{2} \quad (1.2)
\end{align}
$$
ここでクエリ$q$とベクトル$\mathbf{x}_{i}$のユークリッドノルムが定数$C_1, C_2$を用いて$||q||^{2}=C_1, \, ||\mathbf{x}_{i}||^{2}=C_2$のように表せるとき、$(1.2)$式は下記のように同値変形できる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} ||q \, – \, \mathbf{x}_{i}||^{2} &= \mathrm{argmin}_{i}^{(K)} (q \, – \, \mathbf{x}_{i})^{\mathrm{T}} (q \, – \, \mathbf{x}_{i}) \\
&= \mathrm{argmin}_{i}^{(K)} \left( ||q||^{2} \, – \, 2 q^{\mathrm{T}} \mathbf{x}_{i} + ||\mathbf{x}_{i}||^{2} \right) \\
&= \mathrm{argmin}_{i}^{(K)} \left( C_1 \, – \, 2 q^{\mathrm{T}} \mathbf{x}_{i} + C_2 \right) \\
&= \mathrm{argmin}_{i}^{(K)} \left( – \, 2 q^{\mathrm{T}} \mathbf{x}_{i} \right) \\
&= \mathrm{argmax}_{i}^{(K)} q^{\mathrm{T}} \mathbf{x}_{i} \quad (1.1)
\end{align}
$$
上記より、$\mathbf{x}_{i}$のノルムが同じ場合は「同一のクエリ$q$についてのK-MIPS問題がK-NNS問題に帰着する」ことが確認できる。
MCSSと一致する場合
最大内積探索(MIPS)問題は最大余弦類似度探索(MCSS; Maximum Cosine Similarity Search)とも関連する。NNSと同様に厳密には「ベクトル$\mathbf{x}_{i} \in \mathbb{R}^{D}$が同じユークリッドノルム(Euclidean norm)を持つ場合」にMIPSとMCSSSが一致する。K-MCSSの式はクエリ$q$とベクトル$\mathbf{x}_{i}$間のノルムに着目することで上記のように表すことができる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} \frac{q^{\mathrm{T}} \mathbf{x}_{i}}{||q|| ||\mathbf{x}_{i}||} \quad (1.3)
\end{align}
$$
ここでクエリ$q$とベクトル$\mathbf{x}_{i}$のユークリッドノルムが定数$C_1, C_2$を用いて$||q||^{2}=C_1, \, ||\mathbf{x}_{i}||^{2}=C_2$のように表せるとき、$(1.3)$式は下記のように同値変形できる。
$$
\large
\begin{align}
\mathrm{argmin}_{i}^{(K)} \frac{q^{\mathrm{T}} \mathbf{x}_{i}}{||q|| ||\mathbf{x}_{i}||} &= \mathrm{argmin}_{i}^{(K)} \frac{q^{\mathrm{T}} \mathbf{x}_{i}}{C_1 C_2} \\
&= \mathrm{argmax}_{i}^{(K)} q^{\mathrm{T}} \mathbf{x}_{i} \quad (1.1)
\end{align}
$$
上記より、$\mathbf{x}_{i}$のノルムが同じ場合は「同一のクエリ$q$についてのK-MIPS問題がK-MCSS問題に帰着する」ことが確認できる。
クラスタリングを用いた最大内積探索の効率化
k-means
実際の問題でK-MIPS・K-NNS・K-MCSS問題をそれぞれクエリ$q$とベクトル集合$\mathcal{X} = \{ \mathbf{x}_{1}, \cdots , \mathbf{x}_{n} \}$の総当たりで解こうとすると計算量が大きい場合が多い。
総当たりで計算を行う場合は計算量が大きい一方で正確な結果が得られるが、「検索」のように概ね高い類似性が得られればよく「厳密な正確さ」が必要ない場合も多くある。このような際に、k-means法を用いたクラスタリングに基づく解の近似も有力な手法となる。
具体的には下記のような手順に基づいて近似解を得ることができる。
$[1] \,$ ベクトル集合$\mathcal{X} = \{ \mathbf{x}_{1}, \cdots , \mathbf{x}_{n} \}$をk-means法に基づいて$k$個のクラスタに分類
$[2] \,$ クエリ$q$とクラスタの平均ベクトルの内積 or 類似度を計算、値の大きなクラスタを選択
$[3] \,$ 類似度の高いクラスタからクエリ$q$との類似度が高いベクトル$\mathbf{x}_{i}$を選択
上記の$[1]$は参考論文では下記のようなアルゴリズムの形式で表される。

上記のようにクラスタの平均ベクトルとの内積 or 類似度を計算することによって、計算量を減らすことが可能である。たとえば$10,000$ベクトルを$100$個のクラスタに$100$ずつ分類する場合、類似度の計算回数は$100 \times 2 = 200$であり、総当たりの$10,000$から大きく減らすことができる。
一方で、クエリ$q$がクラスタの境界付近に位置する場合など、必ずしも厳密な結果が得られるわけではないことに注意が必要である。この課題に対してはクラスタを複数選ぶなどの対応策が用いられる場合も多い。
階層k-means
前項で確認を行ったk-meansクラスタリングに基づく近似では「クラスタの数が多い:精度が高いが計算量が多い」、「クラスタの数が少ない:計算量が少ないが精度も低い」というトレードオフがある。この問題については階層k-meansが一つの解決策になりうる。
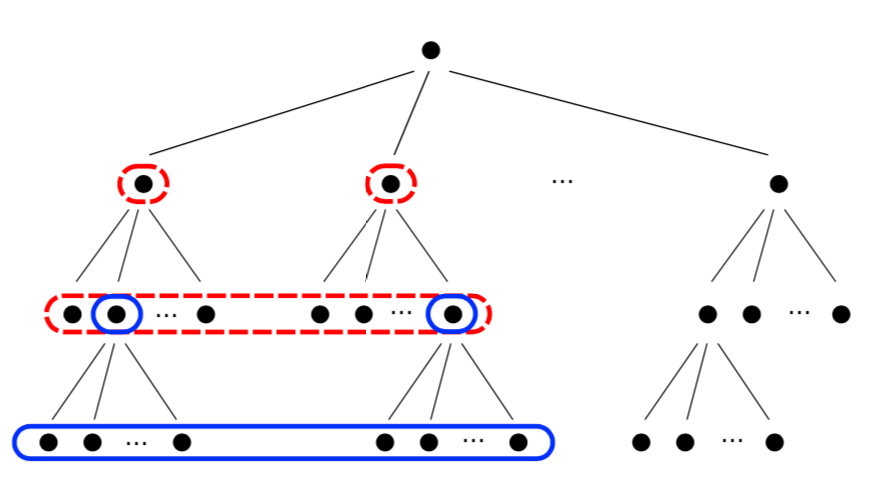
上図のようにベクトルをいくつかの階層型のクラスタに分類しておくことで順々に分類を行うことが可能になる。たとえば$10,000$を$1,000$を$10$個、$1,000$を$10$個、$100$を$10$個のように階層的に分類すると、探索の計算量は$10 \times 4$まで削減できる。
この階層型クラスタは、多くのクラスタを先に作り、徐々に階層型クラスタリングを行うことで構築が可能である。
