DeepLearningに関連する計算にあたってソフトマックス関数(softmax function)はよく出てくる一方で、出力値が過剰になる場合もあり得ます。当記事ではこのような際に値の調整に用いられる温度スケーリング(temperature scaling)の概要と使用例について取りまとめました。
当記事の作成にあたっては、「深層学習 第$2$版」の$7.2$節「注意機構」や$8.3$節「不確かさの予測」の内容などを参考にしました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
温度スケーリングの概要
ソフトマックス関数
$\mathbf{u} = (u_1, \cdots , u_K)$が与えられたとき、ソフトマックス関数$\mathrm{Softmax}(u_k)$は下記のように定義できる。
$$
\large
\begin{align}
\mathrm{Softmax}(u_k) = \frac{\exp{(u_k)}}{\displaystyle \sum_{j=1}^{K} \exp{(u_j)}}
\end{align}
$$
上記の定義より、ソフトマックス関数について下記の式が成立する。
$$
\large
\begin{align}
\mathrm{Softmax}(u_k) & \geq 0 \\
\sum_{j=1}^{K} \mathrm{Softmax}(u_j) &= 1
\end{align}
$$
温度スケーリングによるソフトマックス関数の出力の調整
ソフトマックス関数は$\exp$を用いることで入力値の差を際立たせた出力を行う。たとえば$\mathbf{u} = (5, 6, 7)$が入力の場合、下記の出力が得られる。
import numpy as np
u = np.array([5., 6., 7.])
p_1 = u/np.sum(u)
p_2 = np.exp(u)/np.sum(np.exp(u))
print(p_1)
print(p_2)・実行結果
[ 0.27777778 0.33333333 0.38888889]
[ 0.09003057 0.24472847 0.66524096]計算結果を確認すると、通常の確率化の結果が[ 0.27777778 0.33333333 0.38888889]であるのに対しソフトマックス関数の結果が[ 0.09003057 0.24472847 0.66524096]であり、「緩やかなmax関数」のように解釈することができる。
このようなソフトマックス関数の性質がより必要な時もあればある程度緩和が望ましい場合もあり、このような場合に温度スケーリング(temperature scaling)が用いられる。パラメータ$T$を元に温度スケーリングを施したソフトマックス関数は下記のように定義される。
$$
\large
\begin{align}
\mathrm{Softmax}(u_k) = \frac{\exp{(u_k/T)}}{\displaystyle \sum_{j=1}^{K} \exp{(u_j/T)}} \quad (1)
\end{align}
$$
$T=1$の場合に通常のソフトマックス関数に一致するので$(1)$式はソフトマックス関数の拡張であると理解することもできる。入力値$\mathbf{u} = (5, 6, 7)$に対し$T=0.3, 1, 10$の場合を計算するとそれぞれ下記が得られる。
import numpy as np
u = np.array([5., 6., 7.])
T = np.array([0.3, 1., 10.])
p = np.zeros([T.shape[0], a.shape[0]])
for i in range(T.shape[0]):
p[i,:] = np.exp(u/T[i])/np.sum(np.exp(u/T[i]))
print("T: {:.1f}, p: {}".format(T[0], p[0,:]))
print("T: {:.1f}, p: {}".format(T[1], p[1,:]))
print("T: {:.1f}, p: {}".format(T[2], p[2,:]))・実行結果
T: 0.3, p: [ 0.00122729 0.03440292 0.96436979]
T: 1.0, p: [ 0.09003057 0.24472847 0.66524096]
T: 10.0, p: [ 0.30060961 0.33222499 0.3671654 ]上記より、$T<1$を設定するとより極端な結果が、$T>1$を設定するとより一様分布に近い結果が得られることが確認できる。このようにソフトマックス関数に温度スケーリングを導入することで出力の値を調整することができる。
温度スケーリングの使用例
Transformer
温度スケーリングの導入
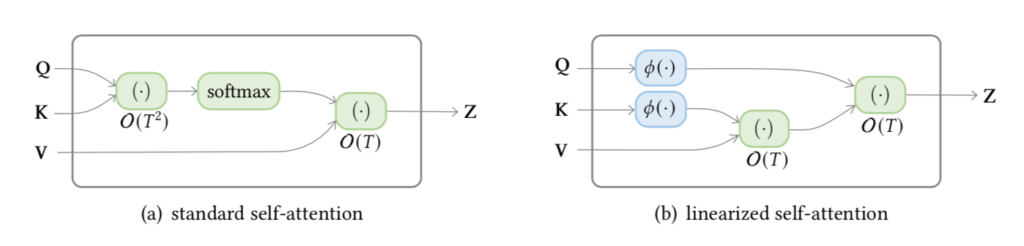
TransformerのDot Product Attentionでは下記のような計算を行う。
$$
\large
\begin{align}
\mathrm{Attention}(Q, K, V) &= \mathrm{Softmax} \left( \frac{Q K^{\mathrm{T}}}{\sqrt{d}} \right) V
\end{align}
$$
$\sqrt{d}$は温度スケーリング$T$と対応させて理解することができる。ここで上記の$d$はトークン毎の次元数に対応するので、「トークン毎の次元が大きい場合は出力を一様な値に調整する」と大まかに解釈することができる。
$\sqrt{d}$を用いる理由の考察
トークン$i$とトークン$j$に対応する中間層のベクトル$\mathbf{v}_{i} \in \mathbb{R}^{d}, \, \mathbf{v}_{j} \in \mathbb{R}^{d}$を下記のように定義する。
$$
\large
\begin{align}
\mathbf{v}_{i} &= \left( \begin{array}{c} v_{i1} \\ \vdots \\ v_{id} \end{array} \right) \\
\mathbf{v}_{j} &= \left( \begin{array}{c} v_{j1} \\ \vdots \\ v_{jd} \end{array} \right)
\end{align}
$$
このとき、$\mathbf{v}_{i}$と$\mathbf{v}_{j}$の内積$\mathbf{v}_{i} \cdot \mathbf{v}_{j}$は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{v}_{i} \cdot \mathbf{v}_{j} &= \left( \begin{array}{c} v_{i1} \\ \vdots \\ v_{id} \end{array} \right) \cdot \left( \begin{array}{c} v_{j1} \\ \vdots \\ v_{jd} \end{array} \right) \\
&= v_{i1} v_{j1} + \cdots + v_{id} v_{jd} \\
&= x_{1} + \cdots + x_{d} = \sum_{k=1}^{d} x_{k}
\end{align}
$$
上記では式の簡略化にあたって、$x_{k} = v_{ik} v_{jk}$を導入した。ここで$x_{k} \sim \mathcal{N}(0, \sigma^{2}), \, \mathrm{i.i.d.}$を仮定すると、$\displaystyle S = \sum_{k=1}^{d} x_{k}$について正規分布の再生性に基づいて下記が成立する1。
$$
\large
\begin{align}
S \sim \mathcal{N}(0, d \sigma^{2})
\end{align}
$$
よって、$S$の標準偏差は$x_{k}$の標準偏差の$\sqrt{d}$倍になる。この結果から、「Transformerにおける温度スケーリングは計算される内積の標準偏差をトークンの次元$d$に依らず一定に保つ目的で導入された」と大まかに解釈できる。
期待校正誤差に基づくソフトマックス出力の校正
DeepLearningの確信度
入力$\mathbf{x}$に対しDeepLearningのソフトマックス演算後の出力を$p(\mathcal{C}_{k}|\mathbf{x})$とおく。この$p(\mathcal{C}_{k}|\mathbf{x})$を「DeepLearningの推論における確信度(confidence)」というが、入力$\mathbf{x}$が得られた際の事後確率と解釈することもできる。
DeepLearningではこの確信度(confidence)は正答率(accuracy)に対し過剰になる場合が多いので注意が必要である。このような場合に用いられる「確信度と正答率が概ね一致するかを確認する指標」の$1$つに期待校正誤差(ECE; Expected Calibration Error)という尺度がある。
以下、期待校正誤差の定義について確認を行う。まず、$N$個のテストサンプルを$M$分割した確信度の範囲$[0,1]$の各区間に分類を行うとき、$M$分割した区間は下記のように表される。
$$
\large
\begin{align}
m = 1 &: \left[ 0, \frac{1}{M} \right] \\
m = 2 &: \left[ \frac{1}{M}, \frac{2}{M} \right] \\
m = 3 &: \left[ \frac{2}{M}, \frac{3}{M} \right] \\
& \vdots \\
m = M-1 &: \left[ \frac{M-2}{M}, \frac{M-1}{M} \right] \\
m = M &: \left[ \frac{M-1}{M}, 1 \right]
\end{align}
$$
このとき$[0,1]$を$M$分割した中の$m$番目のビンに含まれるサンプル集合を$B_{m}$、$B_{m}$に含まれるサンプルの確信度を$\mathrm{conf}(B_{m})$とおくと、$\mathrm{conf}(B_{m})$は大まかに下記の式で近似することが可能である。
$$
\large
\begin{align}
\mathrm{conf}(B_{m}) \simeq \frac{m \, – \, 1/2}{M}
\end{align}
$$
たとえば、$M=10$のとき$m=1, \cdots , 10$について$\mathrm{conf}(B_{m})$の近似値は下記のように計算できる。
| $m$ | $\mathrm{conf}(B_{m})$の近似値 |
|---|---|
| $m=1$ | $\displaystyle \frac{1 \, – \, 1/2}{10} = 0.05$ |
| $m=2$ | $\displaystyle \frac{2 \, – \, 1/2}{10} = 0.15$ |
| $m=3$ | $\displaystyle \frac{3 \, – \, 1/2}{10} = 0.25$ |
| $\vdots$ | $\vdots$ |
| $m=9$ | $\displaystyle \frac{9 \, – \, 1/2}{10} = 0.85$ |
| $m=10$ | $\displaystyle \frac{10 \, – \, 1/2}{10} = 0.95$ |
$\mathrm{conf}(B_{m})$の値は上記のように近似することが可能だが、各テストサンプルの確信度の平均を計算しても良い。ここでは「深層学習 第$2$版」の内容に基づいて近似式を詳しく確認した。
期待校正誤差の定義
「DeepLearningの確信度」で定義したビン$m$に含まれるサンプル集合$B_{m}$の正答率を$\mathrm{acc}(B_{m})$、確信度を$\mathrm{conf}(B_{m})$のようにおく。このとき期待校正誤差$\mathrm{ECE}$は下記のように定義される。
$$
\large
\begin{align}
\mathrm{ECE} = \sum_{m=1}^{M} \frac{|B_{m}|}{N} \left| \mathrm{acc}(B_{m}) \, – \, \mathrm{conf}(B_{m}) \right| \quad (2)
\end{align}
$$
上記の$|B_{m}|$はビン$m$に含まれるテストサンプルの数、$N$は全テストサンプルの数にそれぞれ対応する。
温度スケーリングを用いたソフトマックス出力の調整
バリデーション2データ上で$(2)$式を計算し、$\mathrm{ECE}$の値が最小になるように下記の$T$を調整し、学習を行うことで正答率に対し確信度が過剰になることを防ぐことができる。
$$
\large
\begin{align}
\mathrm{Softmax}(u_k) = \frac{\exp{(u_k/T)}}{\displaystyle \sum_{j=1}^{K} \exp{(u_j/T)}}
\end{align}
$$
