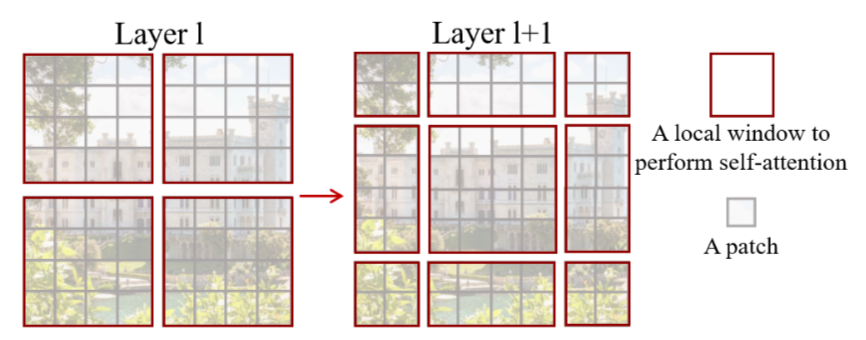
Object Detectionタスクには従来VGGNetやResNetなどのCNNをbackboneに持つネットワークを用いることが主流であった一方で、近年Transformerの導入も行われています。当記事ではObject DetectionにTransformerを導入した研究であるDETRについて取りまとめました。
DETRの論文である「End-to-End Object Detection with Transformers」の内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
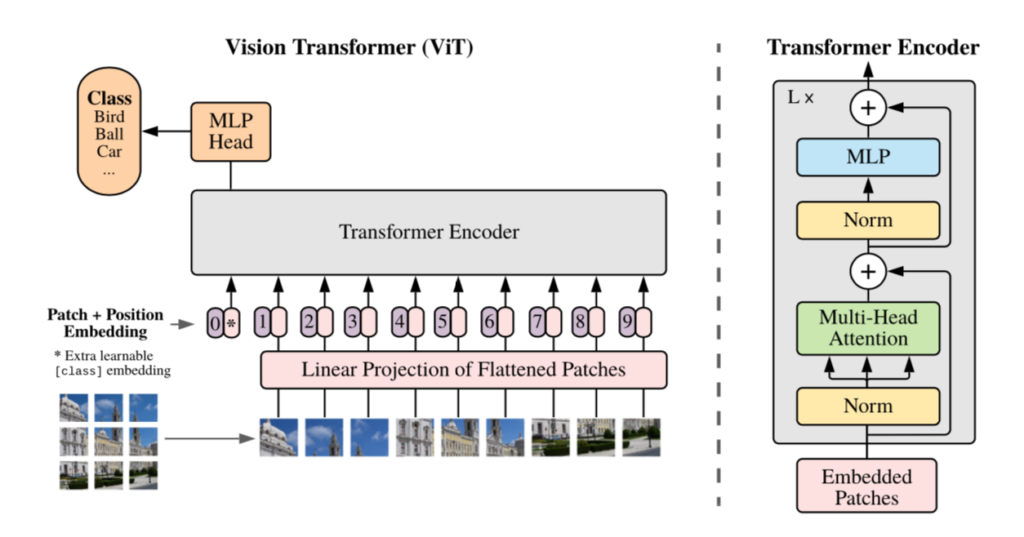
Transformerの概要
Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。
・直感的に理解するTransformerの仕組み(統計の森作成)
指示関数
指示関数(indicator function)の$\mathbb{1}_{[k \neq i]} \in \{ 0, 1 \}$は下記のように定義されます。
$$
\large
\mathbb{1}{[k \neq i]} =
\begin{cases}
1 \quad \mathrm{if} \quad k \neq i \\
0 \quad \mathrm{otherwise}
\end{cases}
$$
Hungarian algorithm
・Hungarian algorithm(Wikipedia)
DETR
処理の概要
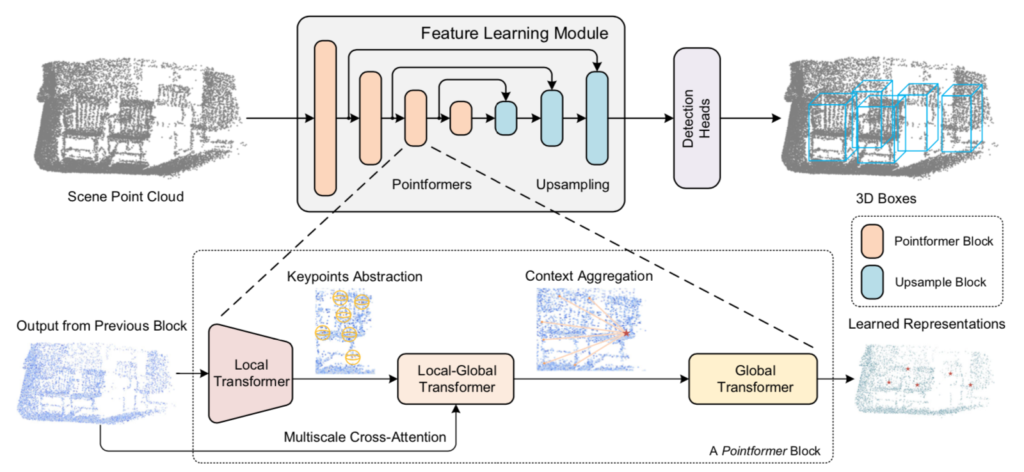
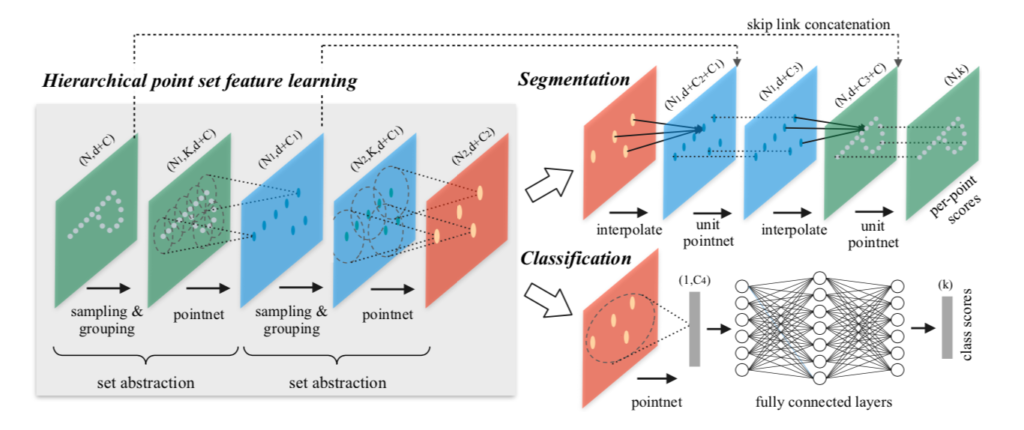
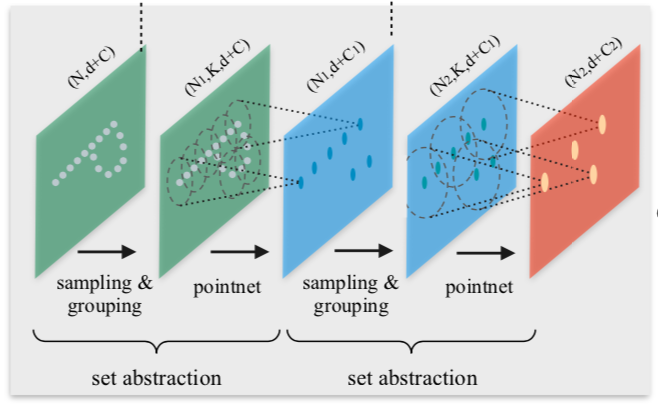
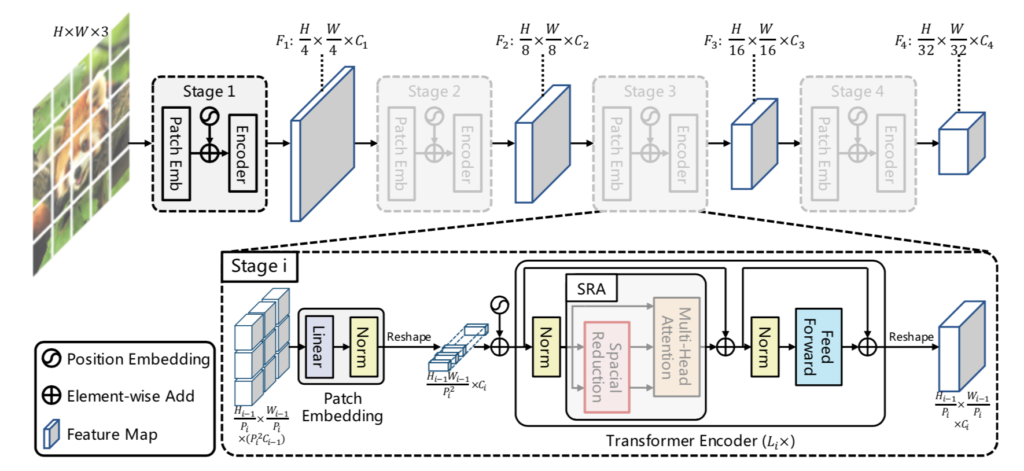
DETR(DEtection TRansformer)の処理の全体は下図より確認できます。
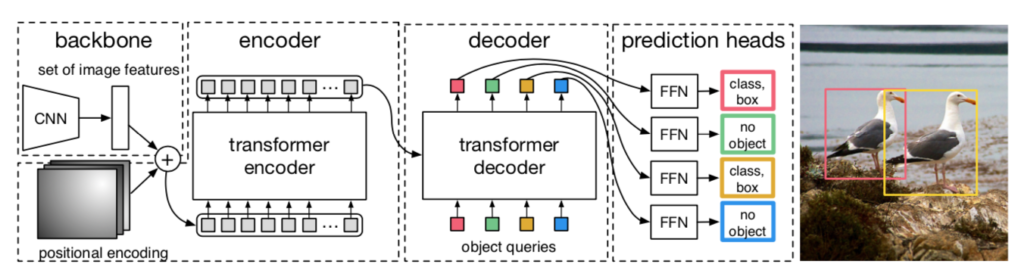
図より、DETRは主に下記の三つのプロセスによって構成されることが確認できます。
・backboneネットワーク
・Transformer
・FFN
以下、それぞれのプロセスの詳細やDETRのlossについて確認を行います。まとめの都合上、「backbone+Transformerのencoder」と「Transformerのdecoder+FFN」に分けて確認を行いました。
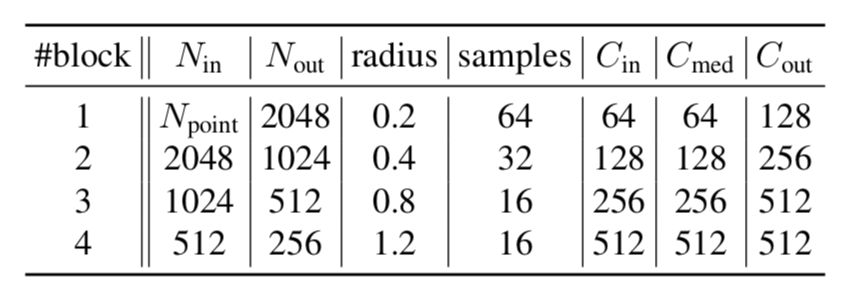
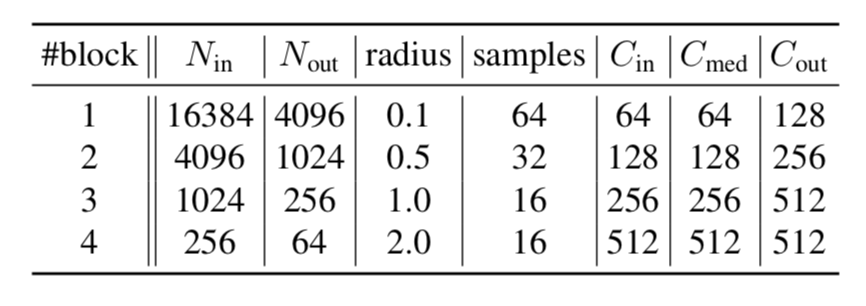
backboneとTransformer encoder
DETRではbackboneネットワークにCNNを用います。
$$
\large
\begin{align}
X_{\mathrm{img}} \in \mathbb{R}^{H \times W \times 3}
\end{align}
$$
上記の入力に対しCNNを作用させ、下記のようなFeature mapを取得します。
$$
\large
\begin{align}
f \in \mathbb{R}^{H \times W \times C}
\end{align}
$$
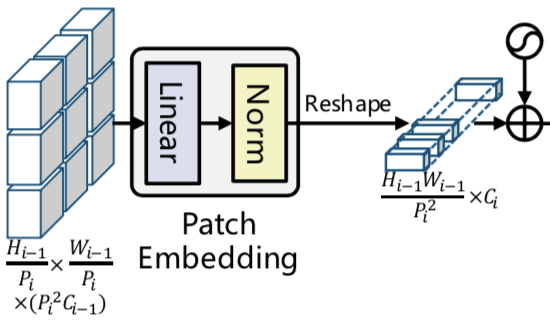
上記のFeature mapに対し、$1 \times 1$のConvolutionを行いReshapeを行った結果の$Z_{0} \in \mathbb{R}^{HW \times d}$をTransformer encoderに入力します。ここで$d$は$d < C$になるように値の設定を行います。
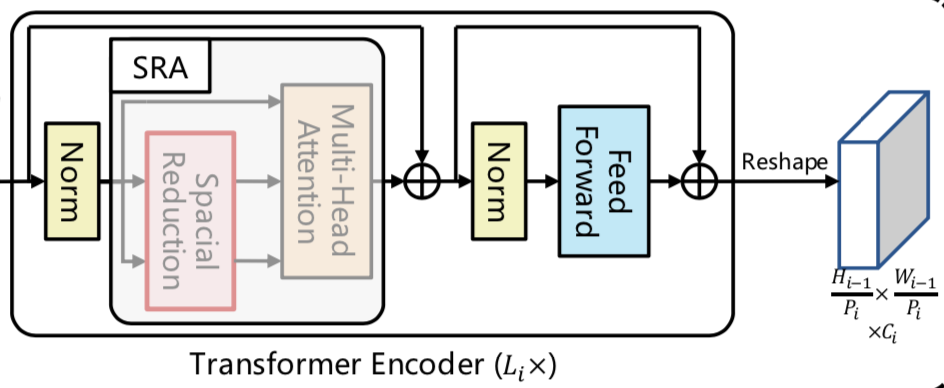
DETRのTransformer encoderはMultiHead AttentionやFFNによって構成されるオーソドックスなTransformerの処理を基本的にそのまま用います。
Transformer decoder: object queriesとbounding boxの生成
Transformer decoderでは機械翻訳では翻訳文が入力されるTransformerのクエリにobject queriesという入力を用います。
このobject queryに基づいてObject Detectionにおけるバウンディングボックスの生成やクラスの予測が行われることから、object queryはFaster-RCNNなどにおけるAnchor boxと同様な役割であると理解すると良いと思います。
ここでobject queryは学習可能なパラメータであり、Faster-RCNN・SSDなど多くのObject Detectionで用いられるAnchor boxをDETRでは自動学習させることができると解釈することもできます。
DETRのloss
$y = \{ y_1, \cdots y_{n} \}, \, y_{n+1} = y_{n+2} \cdots = y_{N-1} = y_{N} = \varnothing$をObject集合の正解、$\hat{y} = \{ \hat{y}_{i} \}_{i=1}^{N} = \{ \hat{y}_{1}, \cdots , \hat{y}_{N} \}$をObjectの予測の集合とおくとき、$y$と$\hat{y}$の最もコストの低い対応を表すインデックスの順列を表す$\hat{\sigma} \in \mathfrak{S}_{N}$は下記のように定義されます。
$$
\large
\begin{align}
\hat{\sigma} &= \mathrm{arg}\min_{\sigma \in \mathfrak{S}_{N}} \sum_{i=1}^{N} \mathcal{L}_{\mathrm{match}}(y_{i}, \hat{y}_{\sigma(i)}) \quad (1) \\
\mathcal{L}_{\mathrm{match}}(y_{i}, \hat{y}_{\sigma(i)}) &= \mathbb{1}_{[c_i \neq \varnothing]} \hat{p}_{\sigma(i)} + \mathbb{1}_{[c_i \neq \varnothing]} \mathcal{L}_{\mathrm{box}}(b_i, \hat{b}_{\sigma(i)})
\end{align}
$$
ここで上記の式における$\mathfrak{S}_{N}$はインデックスの順列の全パターンの集合、$N$は予測の数、$n$は正解のObjectの数、$\mathbb{1}$は指示関数、$\varnothing$は$y_{n+1}$〜$y_{N}$のObjectが存在しないことをそれぞれ表します。
$(1)$式の$\hat{\sigma}$は組み合わせ最適化問題であり、Hungarian algorithmを用いることで得ることができます。ここで得た$\hat{\sigma}$を元にHungarian lossの$\mathcal{L}_{\mathrm{Hungarian}}(y,\hat{y})$は下記のように定義されます。
$$
\large
\begin{align}
\mathcal{L}_{\mathrm{Hungarian}}(y,\hat{y}) &= \sum_{i=1}^{N} \left[ -\log{\hat{p}_{\hat{\sigma}(i)}(c_i)} + \mathbb{1}_{[c_i \neq \varnothing]} \mathcal{L}_{\mathrm{box}}(b_i, \hat{b}_{\sigma(i)}) \right] \quad (2) \\
\mathcal{L}_{\mathrm{box}}(b_i, \hat{b}_{\sigma(i)}) &= \lambda_{\mathrm{IoU}} \mathcal{L}_{\mathrm{IoU}}(b_i, \hat{b}_{\sigma(i)}) + \lambda_{L1}|| b_i-\hat{b}_{\sigma(i)} ||_{1} \\
\lambda_{\mathrm{IoU}}, \lambda_{L1} & \in \mathbb{R}
\end{align}
$$
上記の$c_i, b_i$は$y_i=(c_i,b_i)$によって定義される、Objectの予測のクラスとバウンディングボックスにそれぞれ対応します1。また、$|| \cdot ||_{1}$は$L1$ノルムを表します。
$(2)$式は、「Hungarian algorithmによって得られた$\hat{\sigma}$について、クラス分類に関するCross EntropyとBounding Boxのズレに基づいてlossを定義する」のように解釈することができます。
参考
・Transformer論文:Attention is All you need[$2017$]
・DETR論文
- クラス間不均衡(Class imbalance)に対処するにあたって、実際には$c_i=\varnothing$の場合に$-\log{\hat{p}_{\hat{\sigma}(i)}(c_i)}$をdown-weightします。 ↩︎