DeepLearningなどの機械学習では学習時に用いたサンプルへの過学習(overfitting)が課題になります。当記事ではDeepLearningで過学習を防ぐにあたって導入される正則化(regularization)の手法であるドロップアウトなどについて取りまとめました。
当記事の作成にあたっては、Dropout論文や「深層学習 第$2$版」の第$3$章「確率的勾配降下法」の内容などを参考にしました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
前提の確認
過学習
学習に用いたサンプル以外のサンプルに対し正しく予測が行えることを汎化(generalization)という。関連して訓練データに対する誤差を訓練誤差(training error)、サンプルの母集団に対する誤差の期待値を汎化誤差(generalization error)という。
一方でサンプルの母集団は具体的に得られないので汎化誤差を直接計算することができない。この対応にあたっては学習に用いる訓練データ以外のテスト用データを用意し訓練誤差と同様に誤差を計算することが多い。テストデータを用いて計算される誤差をテスト誤差(test error)という。
汎化誤差を近似し得るテスト誤差の値が訓練誤差の値と大きく乖離することを過剰適合(overfitting)や過学習(overlearning)という。DeepLearningの学習にあたっては過学習が起こらないようにテスト誤差の値をチェックすることが重要になる。
正則化
DeepLearningのようにパラメータが多い際に過学習は生じやすい。この対応にあたっては「学習時にパラメータに一定の制約を課す」ことが多い。このような「パラメータに制約を課すこと」を「正則化(regularization)」という。
正則化の手法は様々であるが、重回帰やロジスティック回帰のような一般化線形モデル(GLM; Generalized Linear Model)の学習の際にはL$2$正則化、CNNの学習ではドロップアウト(dropout)が用いられることが多い。
L2 正則化
パラメータ$\mathbf{w}$によって予測される結果の$n$番目のサンプルの誤差関数(error function)を$E_{n}(\mathbf{w})$、ミニバッチ$\mathcal{D}_{t}$全体の誤差関数を$E_{t}(\mathbf{w})$とおくとき、L$2$正則化に基づいて$E_{t}(\mathbf{w})$は下記のように表される。
$$
\large
\begin{align}
E_{t}(\mathbf{w}) = \sum_{n \in \mathcal{D}_{t}} E_{n}(\mathbf{w}) + \frac{\lambda}{2} ||\mathbf{w}||^{2}
\end{align}
$$
上記の式は第$2$項を追加することにより、パラメータが大きくならないように勾配が生じると解釈すれば良い。$\lambda$は正則化をどのくらい行うかを表すハイパーパラメータである。$\lambda$の値の直感的な解釈にあたって$f(x,y)=(x-1)^{2}+(y-1)^{2}$の正則化を元に以下、確認を行う。
$$
\large
\begin{align}
f(x, y) &= (x-1)^{2}+(y-1)^{2} \\
g(x, y) &= f(x, y) + \frac{\lambda}{2} (x^{2} + y^{2})
\end{align}
$$
上記の例では$f(x, y)$の偏微分が下記のように計算できる。
$$
\large
\begin{align}
\frac{\partial f(x, y)}{\partial x} &= 2(x-1) \\
\frac{\partial f(x, y)}{\partial y} &= 2(y-1)
\end{align}
$$
上記より$(x,y)=(1,1)$で$f(x,y)$は最小値を持つ1。同様に$g(x,y)$の偏微分は下記のように計算できる。
$$
\large
\begin{align}
\frac{\partial g(x, y)}{\partial x} &= 2(x-1) + \lambda x = (2+\lambda)x \, – \, 2 \\
\frac{\partial g(x, y)}{\partial y} &= 2(y-1) + \lambda y = (2+\lambda)x \, – \, 2
\end{align}
$$
上記より$\displaystyle (x,y) = \left( \frac{2}{2 + \lambda}, \frac{2}{2 + \lambda} \right)$で$g(x,y)$は最小値を持つ。
ここで$\lambda = 0, 2$や$\lambda \to \infty$のとき、$\displaystyle (x,y) = \left( \frac{2}{2 + \lambda}, \frac{2}{2 + \lambda} \right)$はそれぞれ下記のように計算できる。
・$\lambda = 0$
$$
\large
\begin{align}
(x,y) &= \left( \frac{2}{2 + \lambda}, \frac{2}{2 + \lambda} \right) \\
&= \left( \frac{2}{2 + 0}, \frac{2}{2 + 0} \right) = (1,1)
\end{align}
$$
・$\lambda = 2$
$$
\large
\begin{align}
(x,y) &= \left( \frac{2}{2 + \lambda}, \frac{2}{2 + \lambda} \right) \\
&= \left( \frac{2}{2 + 2}, \frac{2}{2 + 2} \right) = \left( \frac{1}{2}, \frac{1}{2} \right)
\end{align}
$$
・$\lambda \to \infty$
$$
\large
\begin{align}
(x,y) &= \left( \frac{2}{2 + \lambda}, \frac{2}{2 + \lambda} \right) \\
& \to (0,0)
\end{align}
$$
よって$\lambda = 0$のとき、$g(x,y)$の最小点は$f(x,y)$の最小点に一致し、$\lambda \to \infty$に近づくにつれて徐々に$(0,0)$に近づいていくことが確認できる。このようにL$2$正則化を行うことで、パラメータの大きさに制約を設定することができる。
L$2$正則化(L$2$ regularization)は主に重回帰やGLMの学習にあたって用いられる手法であるが、DeepLearningはGLMの延長と解釈することもできるので、DeepLearningにL$2$正則化を用いること自体はそれほど不自然ではないので合わせて抑えておく必要がある。
DeepLearningの正則化
ドロップアウト
ドロップアウト(dropout)はニューラルネットワークの学習時に中間層の変数をランダムに選別して削除する方法であり、正則化の$1$つに分類される。
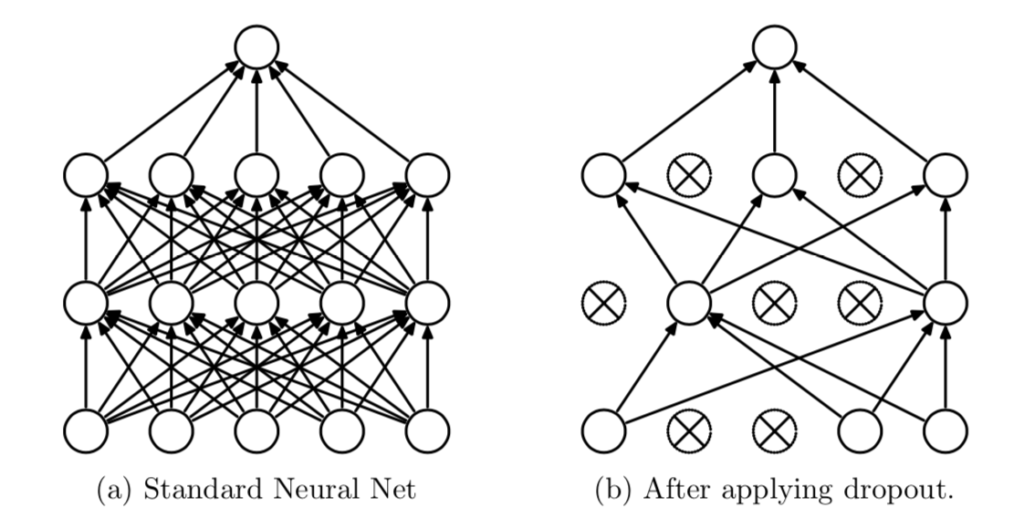
MLP(Multi Layer Perceptron)の学習におけるDropoutを図示すると上図の右のようになる。ドロップアウトの処理は、ランダムフォレストのようなアンサンブル学習と同様に解釈すると良い。
また、学習時の変数の採用確率が$p$のレイヤーでは、推論時に「出力を$p$倍する」か「パラメータを$p$倍する」操作が必要であることも注意しておく必要がある。たとえば$p=0.5$のレイヤーでは推論時の層の出力を$0.5$倍する必要がある。
陰的正則化
確率的勾配降下法(SGD; Stochastic Gradient Descent method)では「全てのサンプルを同時に学習させる」ではなく、「サンプルをランダムに選び学習させる」ということが行われる。
この際に目的関数が変化することで正則化のような効果が得られると解釈が可能である。このように「サンプルをランダムに選び学習させる」ことによって得られる「正則化効果」を「陰的正則化」という。学習の早期終了も陰的正則化の$1$つであると見なすことができる。
- 元の式が平方完成であることに着目すると$(x,y)=(1,1)$が最下点であることが自明であるが、ここでは$g(x,y)$の最小値問題も同じ手法で解くにあたって偏微分の傾きが$0$になる点を取得した。 ↩︎
