統計検定$2$級のCBT(Computer Based Testing)形式の解答例を取りまとめるにあたって、当記事では「統計検定$2$級 公式問題集 CBT対応版」の「PART.$3$ 模擬テスト」の解答例を作成しました。解答例は「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
解答例 Q.1 箱ひげ図より、③が正解である。
Q.2 Ⅰ 正しい
よって④が正解である。
Q.3 Ⅰ 正しい
よって①が正解である。
Q.4 確率変数$Y$の期待値を$E[Y]$、分散を$V[Y]$とおくと、$E[2Y], V[2Y]$は下記のように表せる。
よって変動係数$CV=\sqrt{V[2Y]}/E[2Y]$は下記のように表せる。
上記より$Y$を$2$倍にしても変動係数は変化しない。また、$X,Y$の共分散を$\mathrm{Cov}[X,Y]$とおくとき、$\mathrm{Cov}[X,2Y]$は下記のように表せる。
上記より$Y$を$2$倍すると共分散も$2$倍になる。
以上より、②が正解である。
Q.5 ⑤が正しい。
Q.6 $1,2$回目に$2$連勝するか$2,3$回目に$2$連勝するかのどちらかである。よって確率は下記のように計算できる。
よって⑤が正解である。
Q.7 電気料金の確率変数を$X$とおくと、$X \sim \mathcal{N}(4000,500^2)$である。よって確率$P(X \geq 4800)$の値は$Z \sim \mathcal{N}(0,1)$である確率変数$Z$などを用いることで下記のように得られる。
よって正解は②である。
Q.8 $$
以下、上記を元に$\mathrm{Cov}[X,Y], E[X^2], E[Y^2]$の値の計算を行う。
・$\mathrm{Cov}[X,Y]$
・$E[X^2], E[Y^2]$
$V[W]=V[X-2Y]=4V[X]+V[Y]-4\mathrm{Cov}[X,Y]$より下記が得られる。
$(2)-(1)$より、$3V[X]=12$が得られるので$V[Y]=4$である。ここで$(1)$に$V[X]=4$を代入することで$V[Y]=16$が得られる。$V[X]=E[X^2]-E[X]^2, V[Y]=E[Y^2]-E[Y]^2$が成立するので下記のように$E[X^2], E[Y^2]$の値を計算できる。
以上より、③が正しい。
Q.9 統計量$\displaystyle T = \frac{\overline{X}-\mu}{\sqrt{S^2/16}}$は自由度$15$の$t$分布に従う。よって⑤が正解である。
Q.10 $|\overline{X}-\mu| \leq 0.5$は下記のように考えることができる。
よって、$P(|\overline{X}-\mu| \leq 0.5) \geq 0.95$は下記のように変形できる。
よって正解は④である。
Q.11 標本比率を$\hat{p}$、母比率を$p$とおくと、二項分布の正規近似より下記が成立する。
ここで$p \simeq 0.8$より母比率$p$の$95$%区間に関して下記が成立する。
ここで上記の区間が$6$%以下であるには下記が成立すれば良い。
よって②が正解である。
Q.12 Ⅰ $E[\hat{\mu_1}]=\mu$より$\hat{\mu_1}$は$\mu$の不偏推定量である。
よって⑤が正解である。
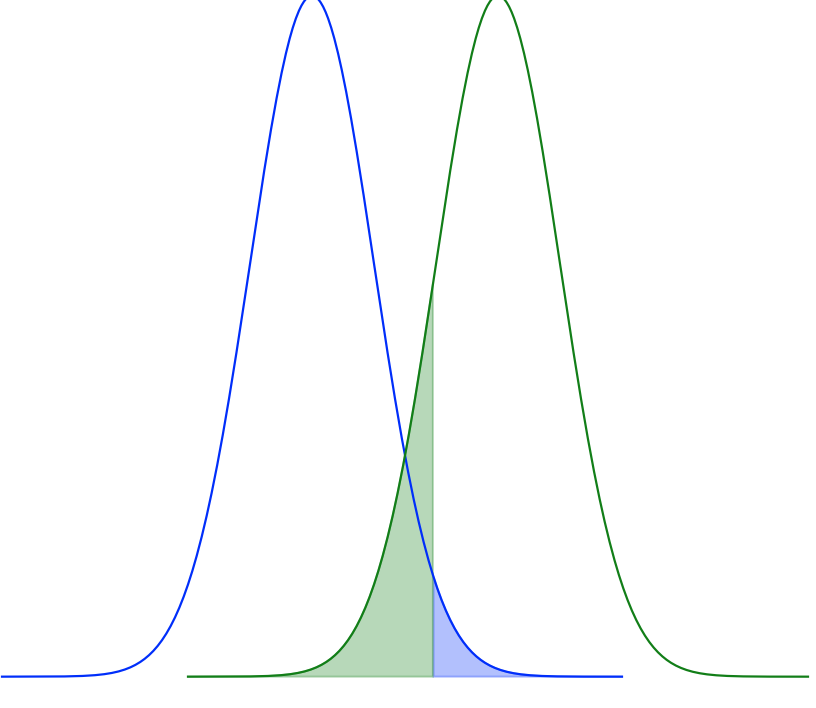
Q.13 第$1$種の過誤の確率$\alpha$は上図の青の領域、第$2$種の過誤の確率$\beta$は上図の緑の領域、にそれぞれ対応すると考えることができる。$H_0: \, \theta=0$、$H_1: \, \theta=1$、棄却域を$x \geq 0.8$のように考えるので、$\alpha, \beta$は統計数値表より、下記のように値が得られる。
上記より②が正解である。
Q.14 検定統計量の実現値$t$は下記のように計算できる。
また、自由度$16-1=15$の$t$分布の上側$5$%点は$t_{\alpha=0.05}(15)=1.753$であるので、$t=1.33 \cdots < 1.753 = t_{\alpha=0.05}(15)$より帰無仮説は棄却されない。
上記より④と⑤に絞られる。ここで④は「変化がないと判断する」、⑤は「変化があると判断できない」とそれぞれ主張されるが、仮説検定の論理展開上、帰無仮説が棄却できる際は「判断を行う」が棄却できない際は「判断を保留する」が適切であるので⑤が適切である。
Q.15 $$
適合度検定の検定統計量は上記のように計算される。ここで$O_i$はそれぞれの観測値、$E_i$は$E_i=147/7=21$が対応するので、④か⑤に絞られる。
また、$\chi^2 \sim \chi^2(6)$であるので、棄却域は$\chi^2 \geq \chi^2_{\alpha=0.05}(6)=12.59$である。よって⑤が正しい。
・参考
import numpy as np
observed_x = np.array([20., 18., 17., 24., 24., 22., 22.])
expected_x = np.repeat(21., 7)
chi2 = np.sum((observed_x-expected_x)**2/expected_x)
print("chi^2: {:.2f}".format(chi2))・実行結果
上記より、帰無仮説は棄却できないことが確認できる。
Q.16 ・$[1]$
・$[2]$
よって②が正解である。
参考 ・【統計検定$2$級対応】統計学入門まとめhttps://www.hello-statisticians.com/stat_basic



![日本統計学会公式認定 統計検定 2級 公式問題集[CBT対応版]](https://m.media-amazon.com/images/I/51q3GfZId3L._SL500_.jpg)