当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$4.4.2$節「対応ある$2$標本の場合」の内容を元に対応のある$2$標本に関する検定について確認を行います。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
「対応ある$2$標本の検定」の概要
概要
| $d_1$ | $65.0$ | $79.3$ | $55.9$ | $73.2$ | $58.0$ | $68.5$ | $68.1$ | $69.9$ | $71.7$ | $58.3$ |
| $d_2$ | $65.1$ | $75.1$ | $49.5$ | $69.9$ | $55.0$ | $64.3$ | $65.3$ | $70.8$ | $75.2$ | $53.5$ |
| $\Delta$ | $0.1$ | $-4.2$ | $-6.4$ | $-3.3$ | $-3.0$ | $-4.2$ | $-2.8$ | $0.9$ | $3.5$ | $-4.8$ |
上記はダイエット処方の効果を確かめるにあたって、処方前の体重$d_1$、処方後の体重$d_2$と体重の変化$\Delta$を表にしたものです。以下、実際の効果を確かめるにあたって、帰無仮説$H_0: \, \Delta=0$と対立仮説$H_1: \, \Delta<0$に関して仮説検定を行います。
このときに$d_1$と$d_2$に相関があり「$4.4.1$ 母平均の差の検定」と同様な手法を用いることはできないので、当記事で以下取り扱う「対応ある$2$標本の取り扱い」の流れを抑えておく必要があります。
必要な数学
$\sqrt{x}$や$x^2$の取り扱いなど、基本的な計算を抑えておけば十分です。
対応ある$2$標本の検定
検定の流れ
前節の$d_1, d_2$の行の値は用いず、$\Delta$の行のみを用います。観測値を$\delta_1, \cdots , \delta_{10}$とおき、下記のように$\bar{\delta}, \hat{\sigma}_{\delta}^{2}$を定義します。
$$
\large
\begin{align}
\bar{\delta} &= \frac{1}{10} \sum_{i=1}^{10} \delta_{i} \\
\hat{\sigma}_{\delta}^{2} &= \frac{1}{9} \sum_{i=1}^{10} (\delta_{i}-\bar{\delta})^2
\end{align}
$$
このとき、下記のように検定統計量の実現値$t$を計算します。
$$
\large
\begin{align}
t &= \frac{\bar{\delta}}{\hat{\sigma}_{\delta}/\sqrt{n}} \\
&= \frac{\sqrt{n} \bar{\delta}}{\hat{\sigma}_{\delta}}
\end{align}
$$
上記に対応する統計量が自由度$10-1=9$の$t$分布$t(9)$に従うことを元に仮説検定を行うことができます。
具体的な計算例
対応ある$2$標本の検定法を用いる
前項の式に基づいて下記を実行することで検定を行うことができます。
import numpy as np
from scipy import stats
delta = np.array([0.1, -4.2, -6.4, -3.3, -3.0, -4.2, -2.8, 0.9, 3.5, -4.8])
sigma2 = np.sum((delta-np.mean(delta))**2)/(delta.shape[0]-1.)
t = np.sqrt(delta.shape[0]) * np.mean(delta) / np.sqrt(sigma2)
if stats.t.cdf(t,10-1)<0.05:
print("t: {:.3f}, reject H_0.".format(t))
else:
print("t: {:.3f}, accept H_0.".format(t))・実行結果
t: -2.543, reject H_0.通常の$2$標本の検定を用いる
「$4.4.1$ 母平均の差の検定」の内容に基づいて下記を実行することで検定を行うことができます。
import numpy as np
from scipy import stats
d = np.array([[65.0, 79.3, 55.9, 73.2, 58.0, 68.5, 68.1, 69.9, 71.7, 58.3], [65.1, 75.1, 49.5, 69.9, 55.0, 64.3, 65.3, 70.8, 75.2, 53.5]])
mean_d = np.mean(d,axis=1)
mean_d_mat = np.repeat(mean_d,10).reshape([2,10])
sum_sigma2 = np.sum((d-mean_d_mat)**2,axis=1)
sigma2 = np.sum(sum_sigma2)/(d.shape[1]+d.shape[1]-2.)
t = (mean_d[1]-mean_d[0]) / (np.sqrt(1./d.shape[1] + 1./d.shape[1]) * np.sqrt(sigma2))
if stats.t.cdf(t,10+10-2)<0.05:
print("t: {:.3f}, reject H_0.".format(t))
else:
print("t: {:.3f}, accept H_0.".format(t))・実行結果
t: -0.652, accept H_0.計算結果
「対応ある$2$標本」の検定法を用いた場合結果が有意であり、「通常の$2$標本の検定」を用いるとき有意でない結果が得られました。この解釈に関しては次項で取り扱います。
対応ある2標本の取り扱いの必要性の解釈
標本平均の差$\overline{X}-\overline{Y}$の分散$V[\overline{X}-\overline{Y}]$は$\overline{X}$と$\overline{Y}$に相関がある場合、下記のように表されます。
$$
\large
\begin{align}
V[\overline{X}-\overline{Y}] = V[\overline{X}] + V[\overline{Y}] – 2 \mathrm{Cov}(\overline{X},\overline{Y})
\end{align}
$$
「$4.4.1$ 母平均の差の検定」では$\mathrm{Cov}(\overline{X},\overline{Y})=0$を前提としているので、$V[\overline{X}-\overline{Y}] = V[\overline{X}] + V[\overline{Y}]$のように表されたことに注意が必要です。
このように「対応ある$2$標本」の場合は、$2$つのグループ間に正の相関があると$\overline{X}-\overline{Y}$の分散$V[\overline{X}-\overline{Y}]$が小さくなることに注意が必要です。冒頭の例に対し、$d_1$と$d_2$の散布図を描くと下記が得られます。
import numpy as np
import matplotlib.pyplot as plt
d = np.array([[65.0, 79.3, 55.9, 73.2, 58.0, 68.5, 68.1, 69.9, 71.7, 58.3], [65.1, 75.1, 49.5, 69.9, 55.0, 64.3, 65.3, 70.8, 75.2, 53.5]])
plt.scatter(d[0], d[1])
plt.show()・実行結果
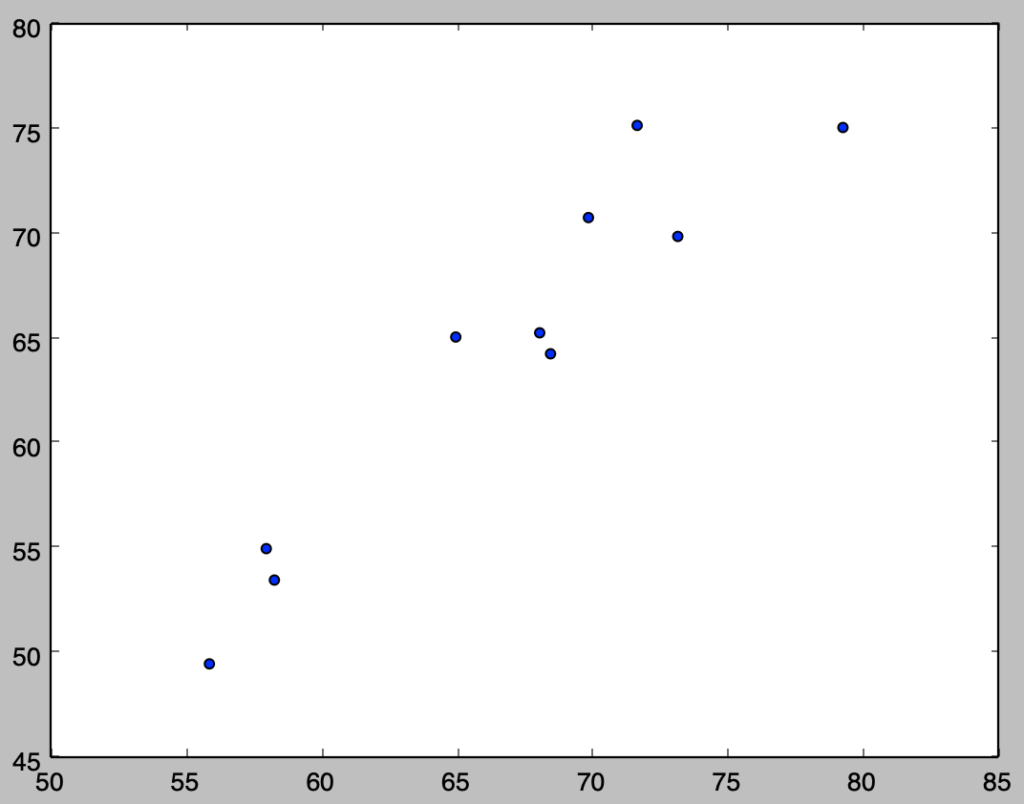
上記のように$2$つの標本には相関があることが確認できます。相関係数は下記のように計算できます。
import numpy as np
d = np.array([[65.0, 79.3, 55.9, 73.2, 58.0, 68.5, 68.1, 69.9, 71.7, 58.3], [65.1, 75.1, 49.5, 69.9, 55.0, 64.3, 65.3, 70.8, 75.2, 53.5]])
mean_d = np.mean(d,axis=1)
mean_d_mat = np.repeat(mean_d,10).reshape([2,10])
cov = np.mean((d[0]-np.mean(d[0]))*(d[1]-np.mean(d[0])))
sigma2 = np.mean((d-mean_d_mat)**2,axis=1)
r = cov / np.sqrt(sigma2[0]*sigma2[1])
print("r: {:.3f}".format(r))・実行結果
r: 0.950ここでの相関係数の値が$0.950$が得られるなど$2$標本間には強相関があるので、前項のような結果が得られたと解釈しておくと良いです。
発展事項①
「通常の$2$標本の検定を用いる」の計算で用いる分散から$2 \mathrm{Cov}(\overline{X},\overline{Y})$分を引いた際の検定は下記のように計算できます。
import numpy as np
from scipy import stats
d = np.array([[65.0, 79.3, 55.9, 73.2, 58.0, 68.5, 68.1, 69.9, 71.7, 58.3], [65.1, 75.1, 49.5, 69.9, 55.0, 64.3, 65.3, 70.8, 75.2, 53.5]])
mean_d = np.mean(d,axis=1)
mean_d_mat = np.repeat(mean_d,10).reshape([2,10])
sum_sigma2 = np.sum((d-mean_d_mat)**2,axis=1)
sum_cov = np.sum((d[0]-np.mean(d[0]))*(d[1]-np.mean(d[0])))
sigma2 = (np.sum(sum_sigma2)-2*sum_cov)/(d.shape[1]+d.shape[1]-2.)
t = (mean_d[1]-mean_d[0]) / (np.sqrt(1./d.shape[1] + 1./d.shape[1]) * np.sqrt(sigma2))
if stats.t.cdf(t,10+10-2)<0.05:
print("t: {:.3f}, reject H_0.".format(t))
else:
print("t: {:.3f}, accept H_0.".format(t))・実行結果
t: -2.543, reject H_0.この結果は「対応ある$2$標本の検定法を用いる」の結果と一致します。
発展事項②
$$
\large
\begin{align}
V[\overline{X}-\overline{Y}] = V[\overline{X}] + V[\overline{Y}] – 2 \mathrm{Cov}(\overline{X},\overline{Y})
\end{align}
$$
上記の式の導出は下記などで取り扱いました。
