数理統計学の教科書・参考書では$\chi^2$分布、$t$分布、$F$分布の確率密度関数の導出に関して解説されますが、累積分布関数に相当する統計数値表の作成にあたっては取り扱われません。そこで当記事では台形公式に基づいて確率密度関数を元に統計数値表の作成に関して取りまとめました。
「現代数理統計学(学術図書出版社)」、「数理統計学(共立出版)」、「統計学のための数学入門$30$講(朝倉書店)」などを参考に作成を行いました。
・統計学に関するPythonプログラミング集
https://www.hello-statisticians.com/stat_program
Contents
基本方針
標本分布の確率密度関数
標本関数の確率密度関数はそれぞれ下記のように表される。
・自由度$n$の$\chi^2$分布$\chi^2(n)$の確率密度関数
自由度$n$の$\chi^2$分布$\chi^2(n)$の確率密度関数を$f(z)$とおくと$f(z)$は下記のように表せる。
$$
\large
\begin{align}
f(z) = \frac{1}{2^{n/2} \Gamma(n/2)} z^{\frac{n}{2}-1} \exp{\left( -\frac{z}{2} \right)}
\end{align}
$$
・自由度$n$の$t$分布$t(n)$の確率密度関数
自由度$n$の$t$分布$t(n)$の確率密度関数を$f(z)$とおくと$f(z)$は下記のように表せる。
$$
\large
\begin{align}
f(z) = \frac{1}{\sqrt{n} B(1/2,n/2)} \left( 1+\frac{z^2}{n} \right)^{-\frac{n+1}{2}}
\end{align}
$$
・自由度$m,n$の$F$分布$F(m,n)$の確率密度関数
自由度$m,n$の$F$分布$F(m,n)$の確率密度関数を$f(z)$とおくと$f(z)$は下記のように表せる。
$$
\large
\begin{align}
f(z) = \frac{z^{\frac{m}{2}-1}}{B(m/2,n/2)} \left( \frac{m}{n} \right)^{\frac{m}{2}} \left( 1+\frac{m}{n}z \right)^{-\frac{m+n}{2}}
\end{align}
$$
数値積分と台形公式
台形公式に基づいて関数$f(x)$の区間$[a,b]$における定積分の近似は下記のように考えることができる。
$$
\large
\begin{align}
\int_{a}^{b} f(x) dx & \simeq \frac{b-a}{2n} [y_0 + 2(y_1 + y_2 + \cdots y_{n-1}) + y_n] \\
y_k &= f(x_k) \\
x_k &= a + \frac{k(b-a)}{n}, \quad k=0, 1, \cdots , n
\end{align}
$$
詳しくは下記で取り扱った。
精度的には台形公式ではなくシンプソンの公式などを用いるべきだが、直感的な理解が目的であれは微小区間の設定次第で精度的には十分であると考えた。台形の公式をそのまま用いたので、算数や初等の数学と同様に理解することができる。
台形公式の使用例:標準正規分布$\mathcal{N}(0,1)$
$$
\begin{align}
\Phi(x) &= \int_{-\infty}^{\infty} f(x) dx \\
f(x) &= \frac{1}{\sqrt{2 \pi}} \exp{ \left( -\frac{x^2}{2} \right) }
\end{align}
$$
標準正規分布$\mathcal{N}(0,1)$の確率密度関数を$f(x)$とおくとき、$f(x)$は上記のように表せる。ここで$f(x)$に対し下記を実行することで台形公式に基づいて統計数値表の近似を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
x = np.arange(-25., 25., 0.01)
f_x = np.e**(-x**2/2.)/np.sqrt(2*np.pi)
delta = 0.01
cum_prob = np.zeros(x.shape[0])
for i in range(x.shape[0]-1):
cum_prob[i+1] = cum_prob[i] + (f_x[i]+f_x[i+1])*delta/2.
plt.subplot(211)
plt.plot(x[2000:-2000],f_x[2000:-2000])
plt.xlim([-5,5])
plt.subplot(212)
plt.plot(x[2000:-2000],cum_prob[2000:-2000])
plt.plot(x[2000:-2000],0.975*np.ones(x[2000:-2000].shape[0]),"g--")
plt.xlim([-5,5])
plt.show()・実行結果
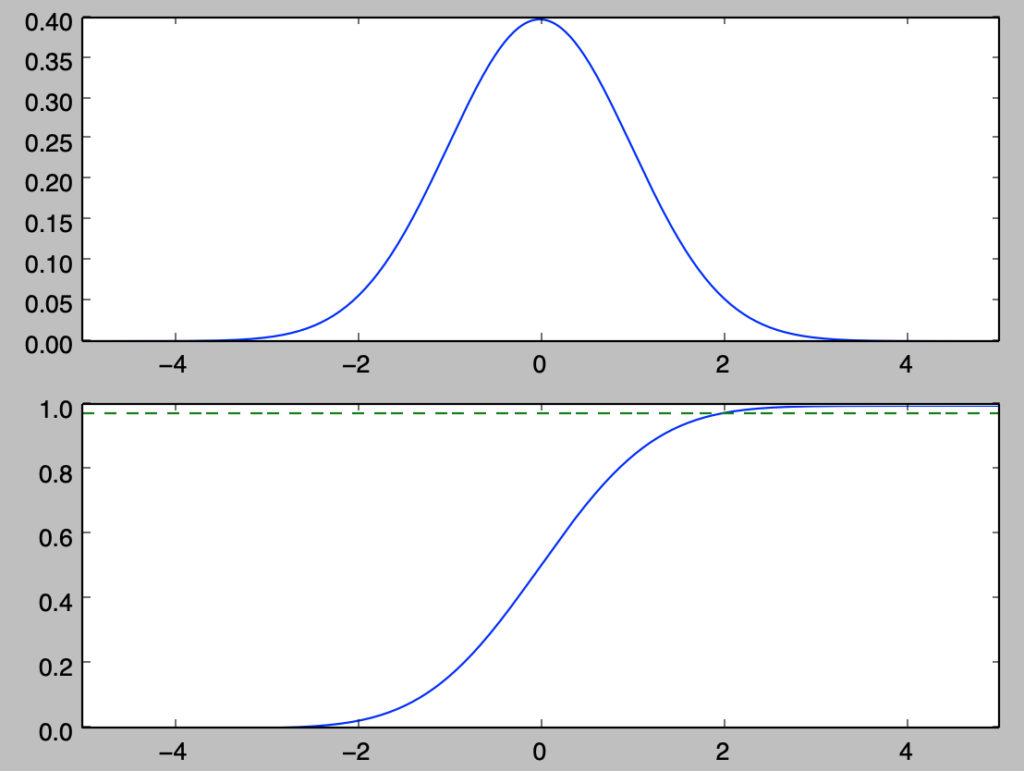
また、台形公式に基づく計算にあたっては標準正規分布の累積分布関数に関して$\Phi(-25) \simeq 0$と見なせることを用いた。より厳密に計算する際は$\Phi(0)=0.5$を元に$0$からの積分を考えると良い。
標本分布の統計数値表
自由度$n=10$の$\chi^2$分布$\chi^2(10)$
自由度$n=10$の$\chi^2$分布$\chi^2(10)$の確率密度関数$f(z)$は下記のように考えることができる。
$$
\large
\begin{align}
f(z) &= \frac{1}{2^{n/2} \Gamma(n/2)} z^{\frac{n}{2}-1} \exp{\left( -\frac{z}{2} \right)} \\
&= \frac{1}{2^{10/2} \Gamma(10/2)} z^{\frac{10}{2}-1} \exp{\left( -\frac{z}{2} \right)} \\
&= \frac{1}{2^{5} (5-1)!} z^{5-1} \exp{\left( -\frac{z}{2} \right)}
\end{align}
$$
上記に基づいて下記を実行することで統計数値表と同様の結果を得ることができる。
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.arange(0., 25., 0.01)
f_x = x**(5-1) * np.e**(-x/2.) /(2**5 * math.factorial(5-1))
delta = 0.01
cum_prob = np.zeros(x.shape[0])
for i in range(x.shape[0]-1):
cum_prob[i+1] = cum_prob[i] + (f_x[i]+f_x[i+1])*delta/2.
plt.subplot(211)
plt.plot(x,f_x)
plt.subplot(212)
plt.plot(x,cum_prob)
plt.plot(x,0.975*np.ones(x.shape[0]),"g--")
plt.show()・実行結果
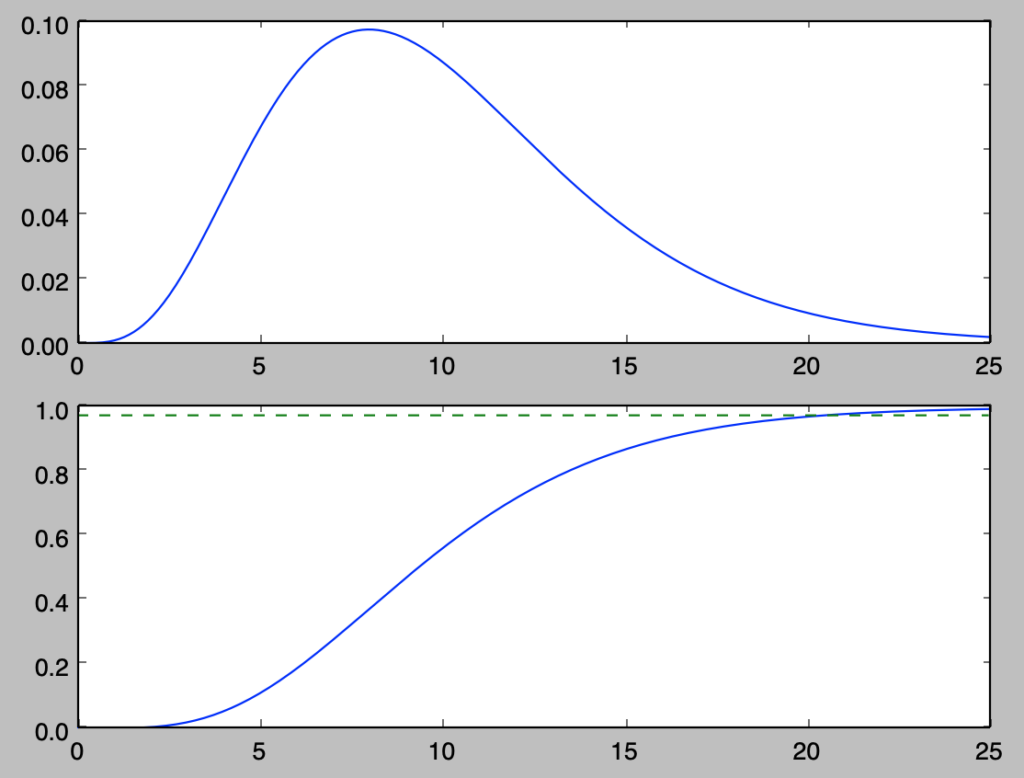
自由度$n=10$の$t$分布$t(10)$
自由度$n=10$の$F$分布$t(10)$の確率密度関数$f(z)$は下記のように考えることができる。
$$
\large
\begin{align}
f(z) &= \frac{1}{\sqrt{n} B(1/2,n/2)} \left( 1+\frac{z^2}{n} \right)^{-\frac{n+1}{2}} \\
&= \frac{\Gamma((n+1)/2)}{\sqrt{n} \Gamma(1/2) \Gamma(n/2)} \left( 1+\frac{z^2}{n} \right)^{-\frac{n+1}{2}} \\
&= \frac{\Gamma((10+1)/2)}{\sqrt{10} \sqrt{\pi} \Gamma(10/2)} \left( 1+\frac{z^2}{10} \right)^{-\frac{10+1}{2}} \\
&= \frac{\Gamma(11/2)}{\sqrt{10} \sqrt{\pi} \Gamma(5)} \left( 1+\frac{z^2}{10} \right)^{-\frac{11}{2}} \\
&= \frac{9!! \cancel{\sqrt{\pi}}}{2^{5} \sqrt{10} \cancel{\sqrt{\pi}} (5-1)!} \left( 1+\frac{z^2}{10} \right)^{-\frac{11}{2}} \\
&= \frac{9!!}{2^{5} \sqrt{10} (5-1)!} \left( 1+\frac{z^2}{10} \right)^{-\frac{11}{2}}
\end{align}
$$
上記に基づいて下記を実行することで統計数値表と同様の結果を得ることができる。
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.arange(-25., 25., 0.01)
f_x = 9.*7.*5.*3.*(1+x**2/10.)**(-11./2.) / (2.**5*np.sqrt(10)*math.factorial(5-1))
delta = 0.01
cum_prob = np.zeros(x.shape[0])
for i in range(x.shape[0]-1):
cum_prob[i+1] = cum_prob[i] + (f_x[i]+f_x[i+1])*delta/2.
plt.subplot(211)
plt.plot(x[2000:-2000],f_x[2000:-2000])
plt.xlim([-5,5])
plt.subplot(212)
plt.plot(x[2000:-2000],cum_prob[2000:-2000])
plt.plot(x[2000:-2000],0.975*np.ones(x[2000:-2000].shape[0]),"g--")
plt.xlim([-5,5])
plt.show()・実行結果
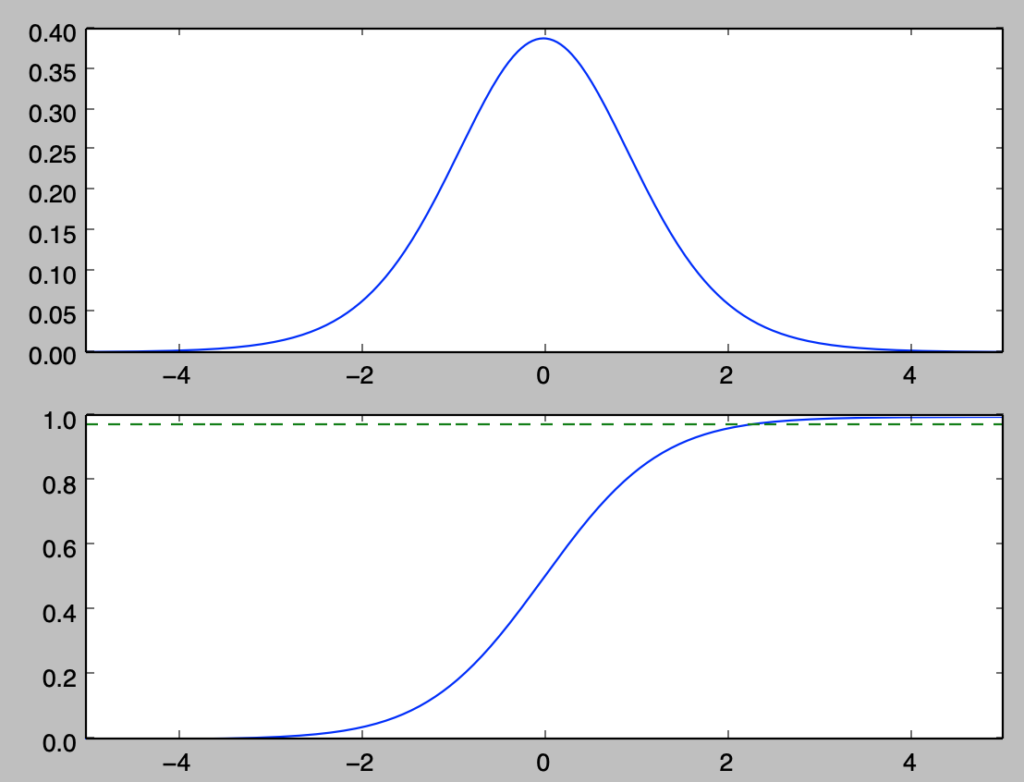
自由度$m=10,n=10$の$F$分布$F(10,10)$
自由度$n=10$の$\chi^2$分布$\chi^2(10)$の確率密度関数$f(z)$は下記のように考えることができる。
$$
\large
\begin{align}
f(z) &= \frac{z^{\frac{m}{2}-1}}{B(m/2,n/2)} \left( \frac{m}{n} \right)^{\frac{m}{2}} \left( 1+\frac{m}{n}z \right)^{-\frac{m+n}{2}} \\
&= \frac{z^{\frac{10}{2}-1}}{B(10/2,10/2)} \left( \frac{10}{10} \right)^{\frac{10}{2}} \left( 1+\frac{10}{10}z \right)^{-\frac{10+10}{2}} \\
&= \frac{z^{5-1}}{B(5,5)} (1+z)^{-10} \\
&= \frac{z^{5-1} \Gamma(5+5)}{\Gamma(5)\Gamma(5)} (1+z)^{-10} \\
&= \frac{z^{5-1} (10-1)!}{(5-1)!(5-1)!} (1+z)^{-10}
\end{align}
$$
上記に基づいて下記を実行することで統計数値表と同様の結果を得ることができる。
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.arange(0., 7., 0.01)
f_x = x**(5-1) * (1+x)**(-10) * math.factorial(5+5-1) / math.factorial(5-1)**2
delta = 0.01
cum_prob = np.zeros(x.shape[0])
for i in range(x.shape[0]-1):
cum_prob[i+1] = cum_prob[i] + (f_x[i]+f_x[i+1])*delta/2.
plt.subplot(211)
plt.plot(x,f_x)
plt.subplot(212)
plt.plot(x[200:],cum_prob[200:])
plt.plot(x[200:],0.975*np.ones(x[200:].shape[0]),"g--")
plt.show()・実行結果
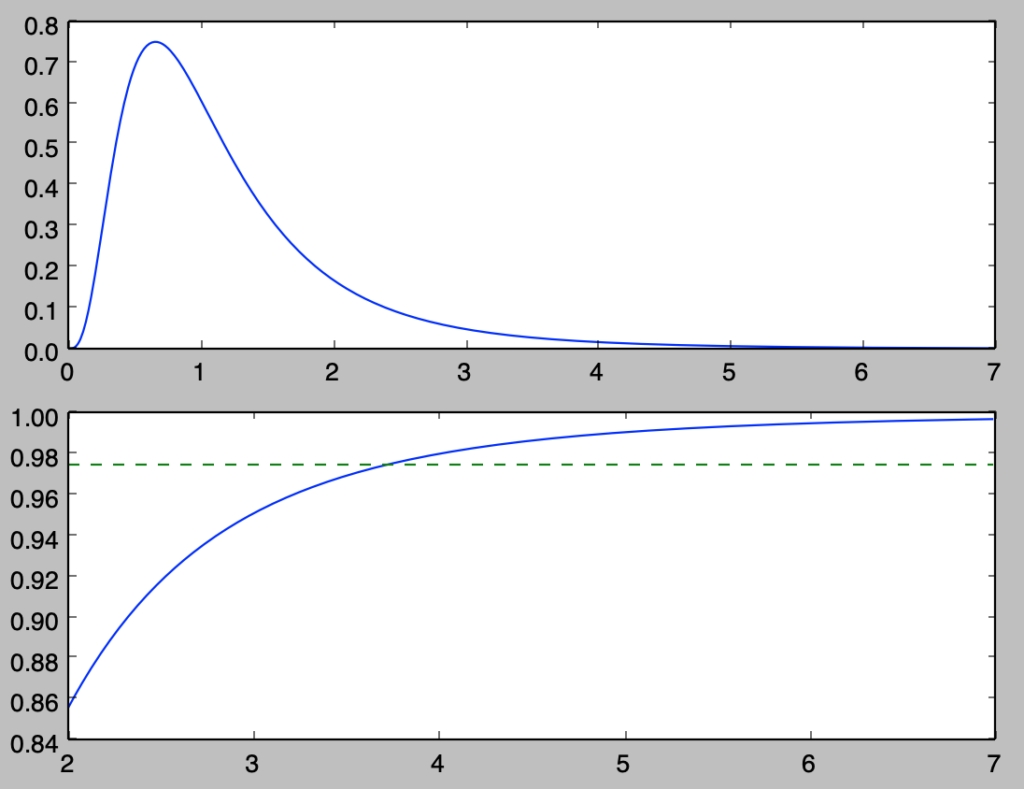

[…] 標本分布の確率密度関数と数値積分による近似に基づく統計数値表の作成 […]
[…] 標本分布の確率密度関数と数値積分による近似に基づく統計数値表の作成 […]
[…] 標本分布の確率密度関数と数値積分による近似に基づく統計数値表の作成 […]