桃太郎電鉄では目的地や特定のマスに到着できるか判定できる機能がありますが、ルート選択が複数あることから判定のアルゴリズムを考えるにあたっては考慮する点が多いです。当記事では特定のマスに到着できるサイコロの目の和を整数に関する問題を解く視点から考察を行いました。
・ゲーム × 統計 まとめ
https://www.hello-statisticians.com/game_stat
Contents
ループの取り扱いに関する基本的な考え方
問題の簡易化
問題の簡易化にあたって、「目的地に対する一番近いルートが得られている際に、より大きな目が出た際に目的地に到着できるか」を一旦取り扱います。
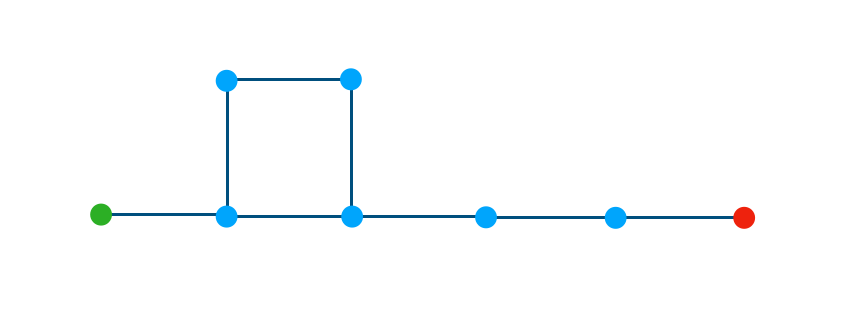
具体的に考えるにあたって、「上記の点間がそれぞれ$1$であるとき緑から赤に到達できる出目」に関して確認します。このとき一番近いルートは$5$であるので、$5$が出れば目的地に到着できます。
ここで注目すべきなのが、途中に存在するループです。たとえば桃太郎電鉄では下記のようなルートを考えることで$7$でも目的地に到着することができます。
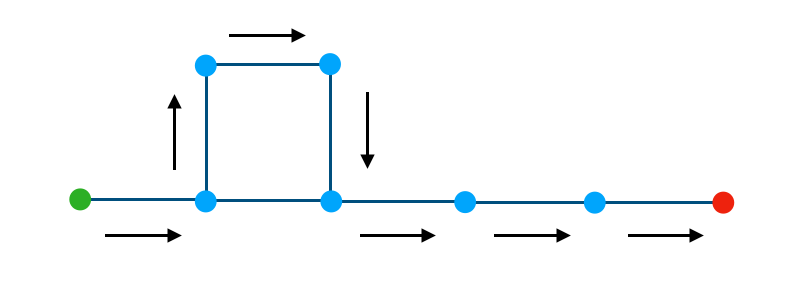
また、下記のように考えることで$9$進む場合も目的地に到着できます。
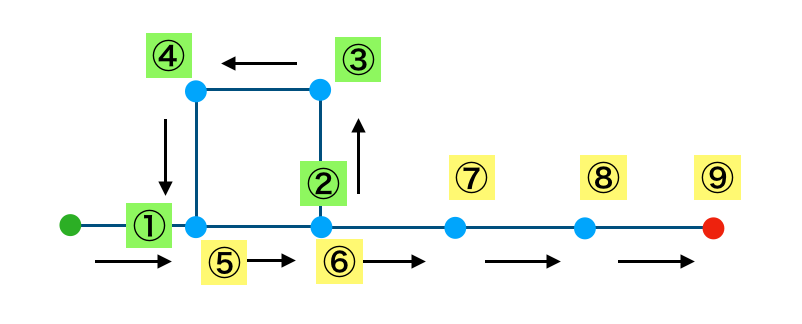
ここで確認した図のように$5$マス先への目的地へのルートに長さ$4$のループが存在する場合は、$7=5+2$と$9=5+4$の場合も目的地に到着できます。また、ループは何度も可能であるので、「$n \geq 0$のときに$5+4n+2, 5+4n$であれば目的地に到着できる」と考えられます。
ここまでで確認を行った考察により、$5$以上の奇数であれば目的地に到着できることから、サイコロを$1$つではなく$2$つ以上用いることで目的地に到着できる確率を上げると考えられます。下記で取り扱った「複数サイコロの出目の確率分布」を考慮することでサイコロの数の最適化を行うことができます。
ここまでは簡単な問題で確認を行いましたが、特に途中で取り扱ったループの取り扱いによって到着可能な出目が左右されます。よって、次節ではループの取り扱いに関して詳しく確認を行います。
ループの取り扱い
ループの長さが変わる場合
前節の例では長さが$4$のループに関して取り扱いましたが、下記のように長さが$5$のループを考えることができます。
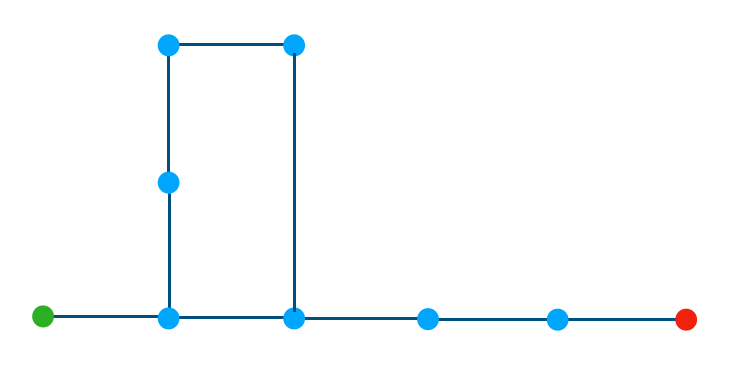
上記では$5, 10, 15, \cdots$と$8, 13, 18, \cdots$の二パターンの到着方法があります。一般的に考える場合は、「$n \geq 0$のときに$5n+5, 5n+8$」であれば目的地に到着できます。
基本的にはループの長さが$4$の場合と同様に考えられますが、「$4n+5, 4n+7$」と「$5n+5, 5n+8$」の対応に関してより詳しく考察を行います。$4n+5$と$4n+7$の差は途中のループエリアを$1+4n$で抜けるか$3+4n$で抜けるかに対応します。
一方で$5n+5, 5n+8$の差は途中のループエリアを$5n+1$で抜けるか$5n+4$で抜けるかに対応します。この考察は次項で確認する「ループがルートに最小で$2$以上含まれる場合」を考える際に重要になります。
ループがルートに最小で$2$以上含まれる場合
前項でも簡単に確認を行いましたが、ルート中にルートが最小でどのくらい含まれるかによって取り扱いが変わることは抑えておくと良いです。たとえば下記のような例を元に考えます。
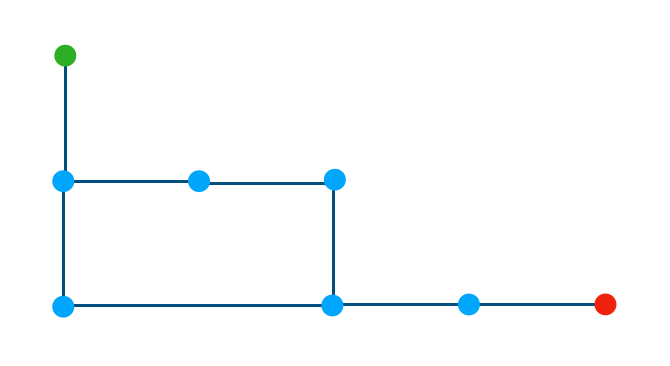
上記の場合、「$n \geq 0$の場合に$5n+5, 5n+6$」で目的地に到着することができます。ここで$5n+5, 5n+6$の差はループ地点を$2$で抜けるか$3$で抜けるかに対応します。
このように「ループの長さ」と同時に「ループがルートに最小でどのくらい含まれるか」の確認が必要です。ループの長さが$4$の場合も同様に確認を行います。
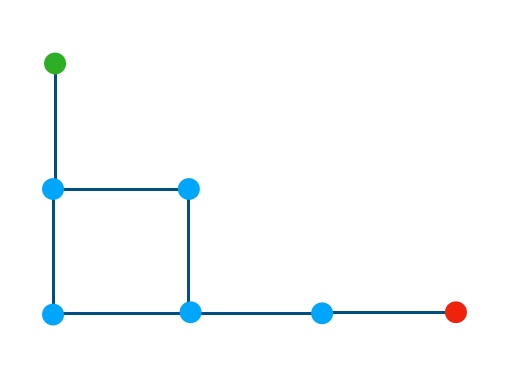
上記の場合は途中のループエリアを$4n+2$でしか抜けられないので、目的地に到達できる出目が$4n+5$のみであることに注意が必要です。より一般的にはループの長さの半分の長さがルートに含まれる場合に同様の事象が起こると把握しておけば良いと思います。
複数ループの取り扱い
当項では複数ループの取り扱いについて確認を行います。基本的には複数ループもループが$1$つの場合と同様に取り扱うことができます。
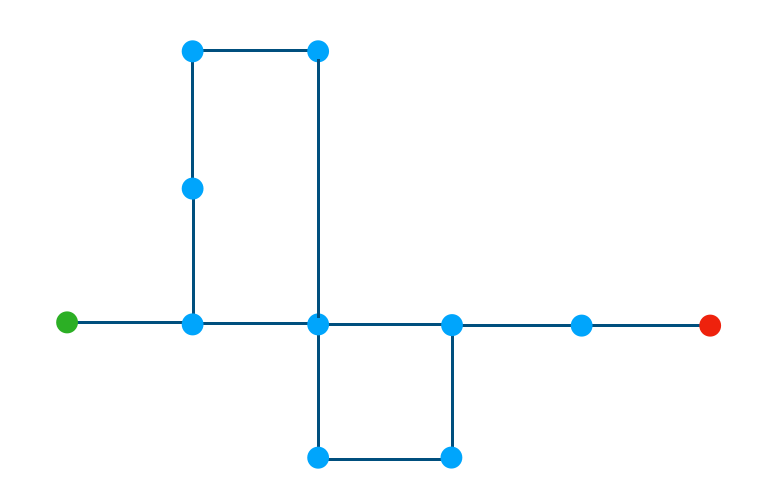
上記のような複数のループがある場合、「長さ$4$のループが経路に$1$含まれる」+「長さ$5$のループが経路に$1$含まれる」と解釈できます。よって、$n \geq 0, m \geq 0$のときに$4n+5, 4n+7$と$5m+5, 5m+8$がそれぞれ目的地に到着できる出目であると考えられます。
上記をまとめると$n \geq 0, m \geq 0$のときに「$4n+5m+5, 4n+5m+7, 4n+5m+8$」で目的地に到着できると考えることができます。また、$m=0, m=1$を元に下記のように考えることができます。
・$m=0$のとき
$$
\large
\begin{align}
4n + 5m + 5 &= 4(n+1) + 1 \\
4n + 5m + 7 &= 4(n+1) + 3 \\
4n + 5m + 8 &= 4(n+2)
\end{align}
$$
・$m=1$のとき
$$
\large
\begin{align}
4n + 5m + 5 &= 4n + 5 + 5 = 4(n+2) + 2 \\
4n + 5m + 7 &= 4n + 5 + 7 = 4(n+3) \\
4n + 5m + 8 &= 4n + 5 + 8 = 4(n+3) + 1
\end{align}
$$
ここで上記の式に$n=0, 1, 2 \cdots$を代入することで、「$7$以上の出目であればどの目が出ても目的地に到着できる」と考えられることは抑えておくと良いと思います。ここまでのループの取り扱いを用いることで、多くのルートを考慮できるので、ループ内のループに関しては一旦省略します。
