桃太郎電鉄のような双六派生のゲームではサイコロの出目を元に駒を進め、勝敗を競います。多くのゲームでは分岐の存在などによる戦略が重要であるので、サイコロの出目の確率に関しては理解しておくと良いです。当記事ではサイコロの出目の確率的な取り扱いに関して取りまとめを行いました。
なお、当記事では考察をシンプルに行うにあたって、サイコロのそれぞれの目の出る確率は同じであると仮定しました。
・ゲーム × 統計 まとめ
https://www.hello-statisticians.com/game_stat
Contents
複数サイコロの取り扱い
サイコロが$1$つの場合
サイコロが$1$つの場合、サイコロの出目の確率変数を$X$とおくと、期待値$E[X]$と分散$V[X]=E[X^2]-E[X]^2$はそれぞれ下記のように計算できます。
$$
\large
\begin{align}
E[X] &= \frac{1}{6} \sum_{x=1}^{6} x \\
&= \frac{21}{6} = \frac{7}{2} \\
V[X] &= E[X^2] – E[X]^2 \\
&= \frac{1}{6} \sum_{x=1}^{6} x^2 – \left( \frac{7}{2} \right)^{2} \\
&= \frac{35}{12}
\end{align}
$$
また、サイコロが$1$つの場合の出目の取り扱いにあたっては多項分布の試行が$1$度の場合に対応するカテゴリ分布を合わせて抑えておくと良いです。
サイコロが$2$つの場合の取り扱い
サイコロが$2$つの場合、サイコロの出目の和を確率変数$X$で表すと、$X$に関する確率関数$p(x)$は下記のように得られます。
| $X$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | $11$ | $12$ |
| $p(x)$ | $\displaystyle \frac{1}{6^2}$ | $\displaystyle \frac{2}{6^2}$ | $\displaystyle \frac{3}{6^2}$ | $\displaystyle \frac{4}{6^2}$ | $\displaystyle \frac{5}{6^2}$ | $\displaystyle \frac{6}{6^2}$ | $\displaystyle \frac{5}{6^2}$ | $\displaystyle \frac{4}{6^2}$ | $\displaystyle \frac{3}{6^2}$ | $\displaystyle \frac{2}{6^2}$ | $\displaystyle \frac{1}{6^2}$ |
このとき期待値$E[X]$はそれぞれ下記のように計算できます。
$$
\large
\begin{align}
& E[X] = \sum_{x=2}^{12} xp(x) \\
&= \frac{1}{6^2}(2+12) + \frac{2}{6^2}(3+11) + \frac{3}{6^2}(4+10) + \frac{4}{6^2}(5+9) + \frac{5}{6^2}(6+8) + \frac{6}{6^2} \cdot 7 \\
&= \frac{2(1+2+3+4+5) + 6}{6^2} \cdot 7 = 7
\end{align}
$$
サイコロが$3$つ以上の場合の取り扱い
サイコロが$3$つの場合の組み合わせと確率
サイコロが$3$つの場合、目の和が$3$〜$10$になる際の出目の組み合わせを列挙すると下記のように表せます。
$$
\large
\begin{align}
3 & \implies 1,1,1 \\
4 & \implies 2,1,1 \\
5 & \implies 3,1,1 \quad 2,2,1 \\
6 & \implies 4,1,1 \quad 3,2,1 \quad 2,2,2 \\
7 & \implies 5,1,1 \quad 4,2,1 \quad 3,3,1 \quad 3,2,2 \\
8 & \implies 6,1,1 \quad 5,2,1 \quad 4,3,1 \quad 4,2,2 \quad 3,2,2 \\
9 & \implies 6,2,1 \quad 5,3,1 \quad 5,2,2 \quad 4,4,1 \quad 4,3,2 \quad 3,3,3 \\
10 & \implies 6,3,1 \quad 6,2,2 \quad 5,4,1 \quad 5,3,2 \quad 4,4,2 \quad 4,3,3
\end{align}
$$
上記の組み合わせに対しそれぞれの並び替えを考えることで、$3$が$1$通り、$4$が$3$通り、$5$が$6$通り、$6$が$10$通り、$7$が$15$通り、$8$が$21$通り、$9$が$25$通り、$10$が$27$通りであることがわかります。このとき確率は下記のように得られます。
| $X$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| $p(x)$ | $\displaystyle \frac{1}{6^3}$ | $\displaystyle \frac{3}{6^3}$ | $\displaystyle \frac{6}{6^3}$ | $\displaystyle \frac{10}{6^3}$ | $\displaystyle \frac{15}{6^3}$ | $\displaystyle \frac{21}{6^3}$ | $\displaystyle \frac{25}{6^3}$ | $\displaystyle \frac{27}{6^3}$ |
また、期待値$E[X]=10.5$を中心に確率は左右対称となるので、$11$〜$18$はここまでの計算結果を逆に並べれば良いです。
Pythonを用いた計算
$6$面ダイスを$3$回振る場合を総当たりで考える場合は$6^3=216$通りを全て考えることでサイコロが$3$つの場合の確率を下記のプログラムで計算できます。
combination_x, prob = {}, {}
for i in range(1*3,6*3+1,1):
combination_x[i], prob[i] = 0, 0
for i in range(6):
for j in range(6):
for k in range(6):
x = i+j+k+3
combination_x[x] += 1
prob[x] += 1.
for i in range(1*3,6*3+1,1):
prob[i] = prob[i]/6.**3
print("Combination x: {}".format(combination_x))
print("Prob: {}".format(prob))・実行結果
Combination x: {3: 1, 4: 3, 5: 6, 6: 10, 7: 15, 8: 21, 9: 25, 10: 27, 11: 27, 12: 25, 13: 21, 14: 15, 15: 10, 16: 6, 17: 3, 18: 1}
Prob: {3: 0.004629, 4: 0.013888, 5: 0.027777, 6: 0.046296, 7: 0.069444, 8: 0.097222, 9: 0.115740, 10: 0.125, 11: 0.125, 12: 0.115740, 13: 0.097222, 14: 0.069444, 15: 0.046296, 16: 0.027777, 17: 0.013888, 18: 0.004629}上記は前項の結果と一致しますが、サイコロを振る数に対応してfor文を用いており、$10$回振る場合に拡張するのが難しいです。よって下記では、サイコロ$n$個の確率分布からサイコロ$n+1$個の確率分布を漸化式的に計算するプログラムを作成しました。
n, m = 3, 6
def extend_dist(dist_dict, m):
new_dist_dict = {}
for i in range(dist_dict.keys()[0]+1,dist_dict.keys()[-1]+1+m):
new_dist_dict[i] = 0
for key in dist_dict.keys():
for i in range(m):
new_dist_dict[key+i+1] += dist_dict[key]/float(m)
return new_dist_dict
prob_init = {}
for i in range(m):
prob_init[i+1] = 1/float(m)
prob = prob_init
if n>1:
for i in range(n-1):
prob = extend_dist(prob, m)
print(prob)・実行結果
Prob: {3: 0.004629, 4: 0.013888, 5: 0.027777, 6: 0.046296, 7: 0.069444, 8: 0.097222, 9: 0.115740, 10: 0.125, 11: 0.125, 12: 0.115740, 13: 0.097222, 14: 0.069444, 15: 0.046296, 16: 0.027777, 17: 0.013888, 18: 0.004629}どちらのプログラムも実行結果は同じですが、「for文をサイコロの数だけ使用する必要がない」点で後者のプログラムが汎用的です。後者のプログラムはパスカルの三角形と同様に理解できるので、下記の図も合わせて確認しておくと良いと思います。
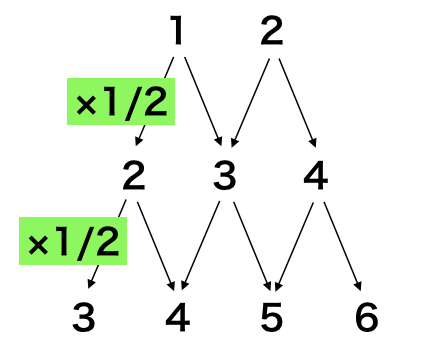
特定のマスに止まるかどうかの取り扱い
双六派生ゲームでは桃太郎電鉄の目的地のように特定のマスに止まるかどうかが重要になる場合があります。したがって以下では一直線にマスが配置された際に特定のマスに止まるかどうかに関する確率に関して考えます。
$1,2$が同じ確率で出る場合
$1,2$が同じ確率で出る場合、特定のマスから$n$マスの状態から特定のマスに止まる確率を$p_n$とおきます。このとき、あと$1$マス、$2$マスの場合はそれぞれ下記のように確率を考えられます。
$$
\large
\begin{align}
p_1 &= \frac{1}{2} \\
p_2 &= \frac{1}{2} + \frac{1}{2} p_1
\end{align}
$$
上記を考えるにあたってはあと$2$マスの場合は$2$が出て直接の場合もあれば$1,1$のように$1$が$2$回出て特定のマスに止まる場合もあることに注意しておくと良いです。また、$p_3$以降は下記のような漸化式で考えることができます。
$$
\large
\begin{align}
p_{n+2} = \frac{1}{2} (p_{n} + p_{n+1}), \quad n \leq 1
\end{align}
$$
漸化式が得られたので、$p_1,p_2,\cdots$はそれぞれ下記のようなプログラムで計算を行うことができます。
p_n1, p_n2 = 1./2., 1./2.+(1./2.)**2
print("p_1: {:.3f}".format(p_n1))
print("p_2: {:.3f}".format(p_n2))
for i in range(15):
p_n, p_n1 = p_n1, p_n2
p_n2 = (p_n+p_n1)/2.
print("p_{}: {:.3f}".format(i+3,p_n2))・実行結果
p_1: 0.500
p_2: 0.750
p_3: 0.625
p_4: 0.688
p_5: 0.656
p_6: 0.672
p_7: 0.664
p_8: 0.668
p_9: 0.666
p_10: 0.667
p_11: 0.667
p_12: 0.667
p_13: 0.667
p_14: 0.667
p_15: 0.667
p_16: 0.667
p_17: 0.667上記の実行結果より、$p_2>p_4>p_6>p_8>\mathrm{others}$であり、あと$2$マスの場合が確率が高く、かつ$n$が大きくなるにつれて確率は$\displaystyle \frac{2}{3}$に近づくことが確認できます。
$6$面ダイスを考える場合
$2$面の場合と同様に漸化式を考えると下記のように表せます。
$$
\large
\begin{align}
p_1 &= \frac{1}{6} \\
p_2 &= \frac{1}{6} + \frac{1}{6} p_1 \\
p_3 &= \frac{1}{6} + \frac{1}{6} (p_1 + p_2) \\
p_4 &= \frac{1}{6} + \frac{1}{6} (p_1 + p_2 + p_3) \\
p_5 &= \frac{1}{6} + \frac{1}{6} (p_1 + p_2 + p_3 + p_4) \\
p_6 &= \frac{1}{6} + \frac{1}{6} (p_1 + p_2 + p_3 + p_4 + p_5) \\
p_{n+6} &= \frac{1}{6} (p_n + p_{n+1} + p_{n+2} + p_{n+3} + p_{n+4} + p_{n+5}), \quad n \leq 1
\end{align}
$$
漸化式が得られたので、$p_1,p_2,\cdots$はそれぞれ下記のようなプログラムで計算を行うことができます。
import numpy as np
p_n = np.zeros([6])+1./6.
for i in range(6):
p_n[i] += np.sum(p_n[:i])/6.
print("p_{}: {:.3f}".format(i+1,p_n[i]))
for i in range(15):
p_n6 = (np.sum(p_n))/6.
p_n[:5] = p_n[1:]
p_n[5] = p_n6
print("p_{}: {:.3f}".format(i+6+1,p_n6))・実行結果
p_1: 0.167
p_2: 0.194
p_3: 0.227
p_4: 0.265
p_5: 0.309
p_6: 0.360
p_7: 0.254
p_8: 0.268
p_9: 0.280
p_10: 0.289
p_11: 0.293
p_12: 0.291
p_13: 0.279
p_14: 0.284
p_15: 0.286
p_16: 0.287
p_17: 0.287
p_18: 0.286
p_19: 0.285
p_20: 0.286
p_21: 0.286上記のように確率が得られました。$p_6$が最大であることは確認しておくと良いと思います。

[…] 双六の派生ゲームにおけるサイコロの確率的取り扱いの考察 〜複数サイコ… […]