当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$2.10.1$節「$\chi^2$分布」の内容に基づいて$\chi^2$分布の定義や確率密度関数のグラフ化に関して取りまとめました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
Contents
$\chi^2$分布の概要
概要
必要な数学
確率密度関数の図示にあたって、指数関数やガンマ関数の理解が必要になります。統計検定$2$級範囲では$\chi^2$分布の確率密度関数は出てきませんが、「統計数値表」の形式で使用する必要があるので確率密度関数の式とグラフの描画に関しては抑えておくと良いと思います。
ガンマ関数の取り扱いに関しては下記で取りまとめました。
$\chi^2$分布
確率変数の対応
$X_i \sim \mathcal{N}(0,1)$が成立するとき、下記のように$Y$を定義します。
$$
\large
\begin{align}
Y = \sum_{i=1}^{n} X_i^2
\end{align}
$$
このとき$Y$は自由度$n$の$\chi^2$分布$\chi^2(n)$に従い、$Y \sim \chi^2(n)$のように表され表されます。
確率密度関数
確率密度関数の数式
自由度$n$の$\chi^2$分布$\chi^2(n)$の確率変数を$Y$、確率密度関数を$f(y)$とおくと、$f(y)$は下記のように表すことができます。
$$
\large
\begin{align}
f(y) = \frac{1}{2^{\frac{n}{2}} \Gamma \left( \frac{n}{2} \right)} y^{\frac{n}{2}-1} \exp \left( -\frac{y}{2} \right)
\end{align}
$$
上記はガンマ分布$\displaystyle \mathrm{Ga} \left( \frac{n}{2},2 \right)$の確率密度関数に一致するので、$\chi^2(n)$はガンマ分布$\displaystyle \mathrm{Ga} \left( \frac{n}{2},2 \right)$に一致します。
ガンマ関数
ガンマ関数$\Gamma(\alpha)$は下記のように定義されます。
$$
\large
\begin{align}
\Gamma(\alpha) = \int_{0}^{\infty} x^{\alpha-1} e^{-x} dx \quad (1)
\end{align}
$$
このとき、ガンマ関数$\Gamma(\alpha)$に関して以下の式が成立します。
$$
\large
\begin{align}
\Gamma(\alpha+1) &= \alpha \Gamma(\alpha), \quad (2) \\
\Gamma(1) &= 1, \quad (3) \\
\Gamma(n) &= (n-1)!, n \in \mathbb{N}, \quad (4) \\
\Gamma \left( \frac{1}{2} \right) &= \sqrt{\pi}, \quad (5)
\end{align}
$$
詳しい導出は下記で取り扱いました。
発展事項①
$\chi^2$分布の確率密度関数の導出にあたっては統計検定準$1$級や$1$級で出てくる変数変換などが必要で難しいので当記事では省略しました。詳しくは下記で取り扱いましたので、導出を確認する際は下記などをご確認ください。
確率密度関数の図示
以下では$\chi^2(1), \chi^2(3), \chi^2(10)$の$\chi^2$分布の図示を行います。それぞれの分布のガンマ関数は前項の式に基づいて下記のように計算できます。
$$
\large
\begin{align}
\Gamma \left( \frac{1}{2} \right) &= \sqrt{\pi} \\
\Gamma \left( \frac{3}{2} \right) &= \frac{1}{2} \Gamma \left( \frac{1}{2} \right) \\
&= \frac{\sqrt{\pi}}{2} \\
\Gamma \left( \frac{10}{2} \right) &= \Gamma(5) \\
&= (5-1)! = 4!
\end{align}
$$
上記より、確率密度関数の式に基づいて下記を実行することで$F$分布の確率密度関数を描くことができます。
import numpy as np
import matplotlib.pyplot as plt
import math
y = np.arange(0.1,20.1,0.01)
f_y = {}
f_y[0] = y**(1./2.-1) * np.e**(-y/2.) / (2**(1./2.) * np.sqrt(np.pi))
f_y[1] = y**(3./2.-1) * np.e**(-y/2.) * 2. / (2**(3./2.) * np.sqrt(np.pi))
f_y[2] = y**(10./2.-1) * np.e**(-y/2.) / (2**(10./2.) * math.factorial(4))
label_y = {}
label_y[0], label_y[1], label_y[2] = "n = 1", "n = 3", "n = 10,"
for i in range(3):
plt.plot(y,f_y[i],label=label_y[i])
plt.legend()
plt.ylim([0.,0.5])
plt.show()・実行結果
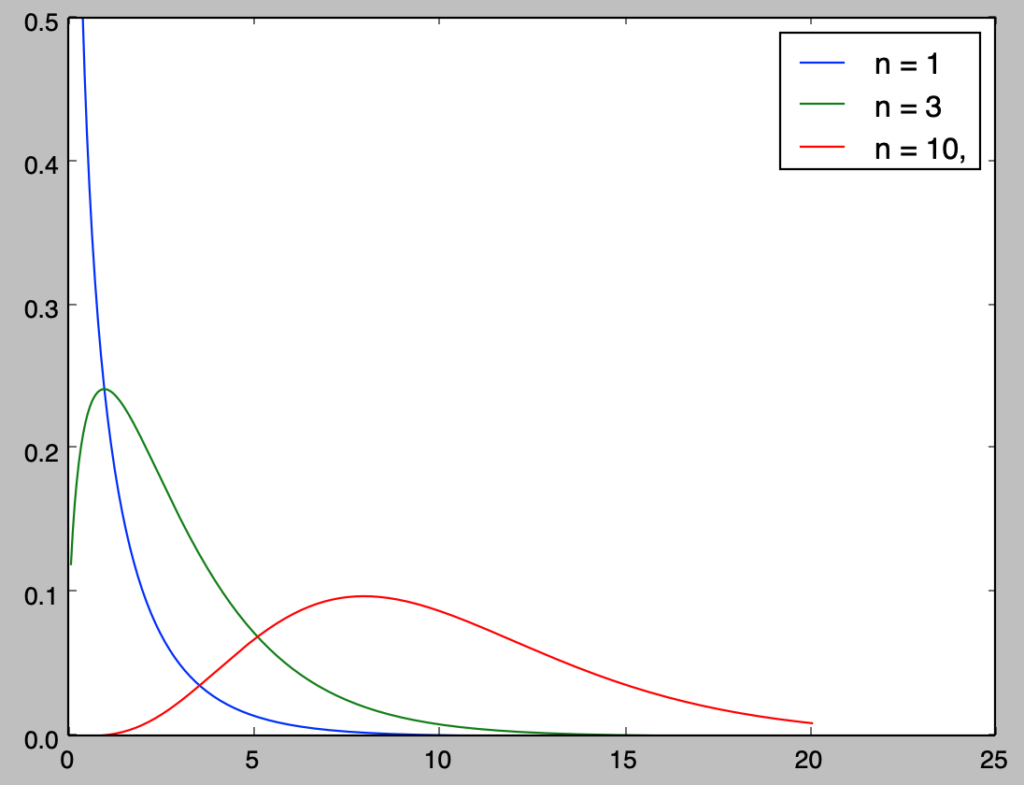
上図は「統計検定$2$級対応 統計学基礎」の図$2.9$に対応します。
発展事項②
標本分布の確率密度関数から「統計数値表」の作成にあたっては「数値積分」が用いられます。教科書などで取り扱われることは少ないですが、台形の公式などに基づいて近似値の計算ができるので、概要は抑えておくと良いかもしれません。
$\chi^2$分布の期待値・分散
自由度$n$の$\chi^2$分布の期待値$E[Y]$と分散$V[Y]$は下記のように表される。
$$
\large
\begin{align}
E[Y] &= n \\
V[Y] &= 2n
\end{align}
$$
上記の詳しい導出は下記で取り扱いました。
