当記事は「倉田+, 入門統計解析 (新世社)」の読解サポートにあたって4章「確率モデル」の演習問題を解説します。
執筆:@masumasumath1
演習問題解答例 問題4.1 問題4.2 問題4.3 問題4.4 問題4.5 4.5.1
まず期待値$E(X)$を求める。
$$
$V(X) = E(X^2) – E(X)^2$を用いて分散を計算する。
$$
従って,分散$V(X)$は
$$
4.5.2
4.5.1と同様に計算すればよい。
$$
期待値の線形性から $E(2X+5) = 2E(X)+5$ であるから$$E(2X+5) = 2E(X)+5 = 2\cdot 0 + 5 = 5$$である。
$$
分散$V(X)$は
$$
4.5.3
$P(-\infty \leq X \leq \infty) = P(0 \leq X \leq 1) = 1$であるから,${\displaystyle \int_{0}^{1} ax^2 dx = 1}$が成り立つ。従って,
$$
となる。よって $a = 3$ である。
$$
4.5.4
ここまでと同様に,
$$
$$
$$
4.5.5
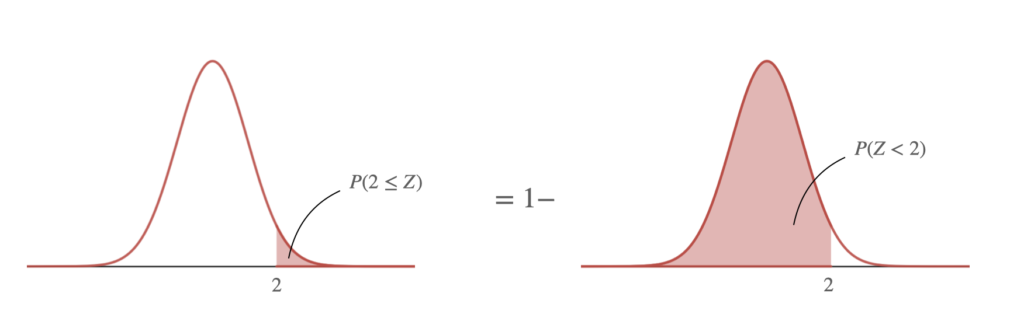
$X$ の基準化変量を $Z$ とすると,${\displaystyle Z = \frac{X-50}{10}}$ であり,$Z \sim N(0,1)$ である.これと正規分布表を利用して値を計算する.
(1)
\begin{eqnarray*}
(2)
\begin{eqnarray*}
※本誌では,正規分布表として,$\Phi(a) = P(X\leq a )$の値が与えられている.それを用いると,
$P(-1 \leq Z \leq 1) = 2\times (P(Z \leq 1)-P(Z \leq 0) ) =2\times (0.841-0.5) $である.正規分布表に応じて計算する.
(3)
$(1)$,$(2)$ と同様に計算すればよい.
$P(X \leq 55) = P(Z \leq 0.5) = 0.691$
4.5.6
ビスの直径を$X$とすると,$X \sim N(2.7998, 0.0005^2)$ である.
ここで$X$ の基準化変量を $Z$ とすると,${\displaystyle Z=\frac{X-2.7998}{0.0005}}$である.
\begin{eqnarray*}
となる.従って,不合格となる割合は$1-0.805 = 0.195$である.
4.5.7
品切れになるのは,(需量要)$\geq$ (在庫量)となるときなので,$P(需要量\geq 在庫量)\leq 0.05$となる条件を求める.つまり,在庫量を$a$とおいて,$P(X\geq a) \leq 0.05$を満たす$a$を求めればよい.
\begin{eqnarray*}
となる.
正規分布表から$P(Z \leq 1.64) \leq 0.95$であるから,これを満たす$a$は ${\displaystyle 1.64 \leq \frac{a-200}{25} }$ を解いて,$241 \leq a$を得る.従って,241(t) 以上あればよい.
4.5.8
$Y=\mu + X = 10 + X$と表される.$X\sim N(0,\sigma^2) = N(0, 0.001^2)$であるから,$Y \sim N(\mu, \sigma^2) = N(10,0.001^2)$である.
4.5.9
国語の成績を$X$(点)とすると,$X \sim N(64,13^2)$である.$ \displaystyle{ Z = \frac{X-64}{13}}$とすると,$Z \sim N(0,1)$である.
(1) $P(64-20 \leq X \leq 64+20 )$を求める.
$$
(2) 上位$5\%$である成績を$a$(点)とすると,$P(X \geq a) = 0.05$が成り立つ.また,$P(X \geq a) = 0.05 \iff P(X \leq a) = 0.95$ である.
(3) $P(X \leq 40)$を求める.
$$
従って,$40$点は下位$3.2\%$である.
4.5.10
次の客が到着するまでの時間間隔が$X$(分)であるから,$X$は指数分布に従う.$1$時間あたり$20$人の客が来るので,$1$分あたり$20/60 = 1/3$(人)が到着する.
$$
であるから,$P(X \geq 5) = 1 – P(X \leq 5) = 1 – (1-e^{-\frac{5}{3}}) = e^{-\frac{5}{3}} \approx 0.189$.
4.5.11
客が到着する時間間隔を$X$(分)とする.$1$時間あたり平均$5$人の客が訪れるので$5/60 = 1/12$(人/分)である.従って,$X \sim Ex(1/12)$である.通常時の開店時刻から$5$分以内に到着していれば,$5$分以上待つことになる.つまり,$P(X \leq 5)$が求める確率であり,その値は
$$
4.5.12
定理4.23(前半)
$X\sim Ex(\lambda)$ のとき,任意の正の実数 $a$,$b$に対して,次が成り立つことを示す.
$$
証明
$X\sim Ex(\lambda)$とする.すると,密度関数$f(x)$は,
$$
である.また,
$$
さらに,$P(X>a+b \land X > b) = P(X>a+b)$であるから,$P(X>b)$と同様にして
$$
がわかる.$P(X>a) = e^{-\lambda a}$も同様.
$$
となり示された.(終)
定理4.24
定義に従ってそれぞれ計算する.
$$
ここで,$y=\lambda x$とおくと,$x=0$とき,$y=0$であり,$\lambda > 0$であるから,$x\rightarrow \infty$のとき,$y \rightarrow \infty$である.また,$dy = \lambda dx$なので
$$
となる.さらに,この右辺の${ \displaystyle\int_0^\infty ye^{-y}dy}$に部分積分を行うことで,
$$
となる.したがって,${\displaystyle E(X) = \frac{1}{\lambda} }$が示された.
$$
である.よって,分散$V(X)$は
$$
となる.
参考 ・抑えておきたい公式とその簡易的な導出に関して(期待値と分散・共分散)https://www.hello-statisticians.com/explain-terms-cat/expectation-variance-covariance.html

![日本統計学会公式認定 統計検定 1級・準1級 公式問題集[2018〜2019年]](https://m.media-amazon.com/images/I/51GLGHCDh7L._SL500_.jpg)

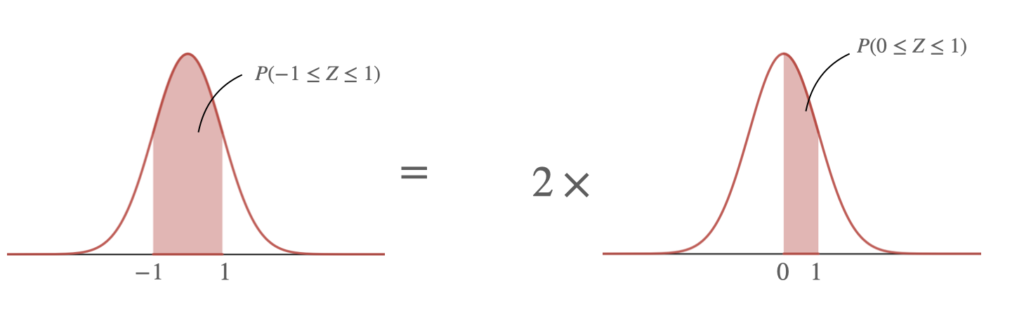









![日本統計学会公式認定 統計検定 2級 公式問題集[2018〜2021年]](https://m.media-amazon.com/images/I/51PRkPbugTL._SL500_.jpg)
![日本統計学会公式認定 統計検定 3級・4級 公式問題集[2018〜2021年]](https://m.media-amazon.com/images/I/51aVZIJSQ2L._SL500_.jpg)