中心極限定理(Central Limit Theory)の概要、活用、導出

中心極限定理(Central Limit Theory)は推測統計の基盤となる大定理ですが、一方で数式が難しそうに見えるかもしれません。そこで当記事では中心極限定理に関して概要や活用、導出を取り扱いました。特に利用にあたっての工夫に関して可能な限りわかりやすく取りまとめを行いました。

中心極限定理の概要

直感的な理解

直感的な理解にあたっては、中心極限定理(Central Limit Theory)は「母集団分布に関係なく、標本の和$X_1+X_2+…+X_n$や標本平均が従う分布は正規分布で近似できる」と理解すると良い。中心極限定理は特性関数などを考えることで示すことができるが、少々難しいので応用上の観点からは「多くのサンプルを観測すれば、その和やその平均は正規分布から観測されたと考えられる」のように、直感的に理解しておくでも十分であると思われる。

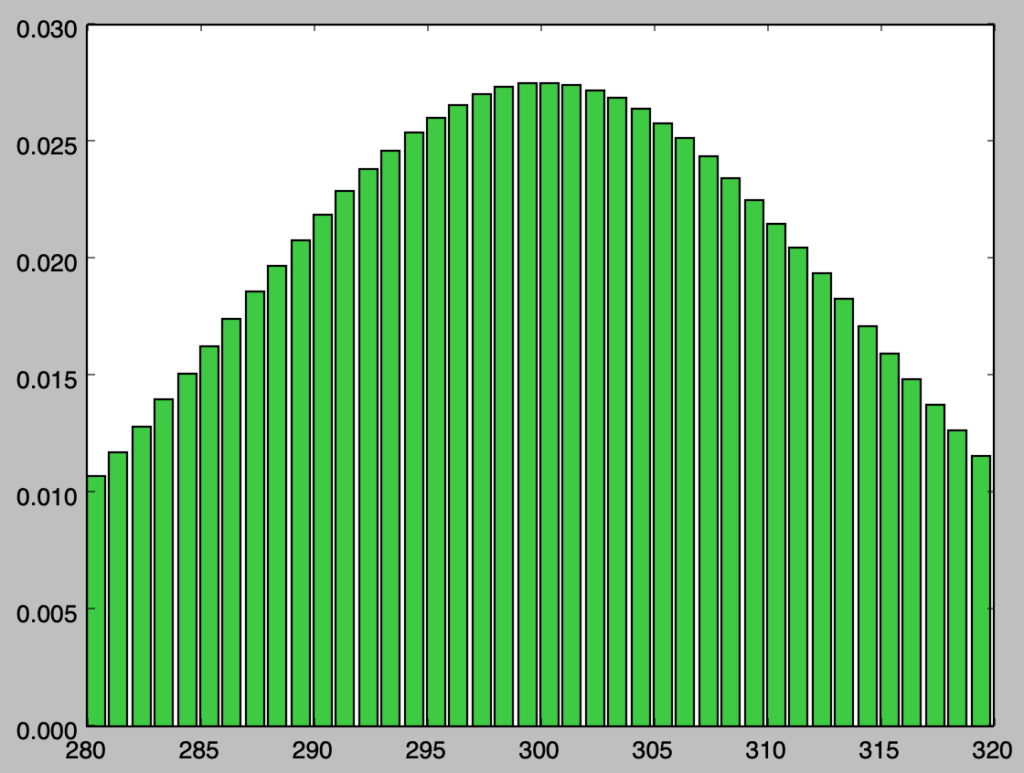
上図のように「二項分布の極限」の「中心極限定理」でPythonを用いていくつか図示化を行なったが、二項分布の観測値は$n$が大きいとき正規分布で近似できる。

数式を用いた中心極限定理の表現

中心極限定理は$E[X_i]=\mu, V[X_i]=\sigma^2$に基づく標本列$X_1, X_2, …, X_n$に対して下記のように定義できる。
$$
\large
\begin{align}
S_n &= \sum_{i=1}^{n} X_n \sim \mathcal{N}(n \mu, n \sigma^2) \\
\overline{X} &= \frac{1}{n} \sum_{i=1}^{n} X_n \sim \mathcal{N} \left( \mu, \frac{\sigma^2}{n} \right)
\end{align}
$$

式の表記に関しては下記の演習でも取り扱ったので、演習を行う際は合わせて確認しておくと良い。

中心極限定理やデルタ法を用いた分布収束｜問題演習で理解する統計学【6】

ここで$\displaystyle \overline{X} \sim \mathcal{N} \left( \mu, \frac{\sigma^2}{n} \right)$は$n \to \infty$のとき$\displaystyle \frac{\sigma^2}{n} \to 0$より、中心極限定理は大数の法則も同時に表すことに関しても抑えておくとよい。

中心極限定理は下記のような形式で標本和$S_n=X_1+X_2+…+X_n$に関して表すこともできる。
$$
\large
\begin{align}
\lim_{n \to \infty} P \left( a \leq \frac{S_n – n \mu}{\sqrt{n}\sigma} \leq b \right) &= \int_{a}^{b} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx \\
&= \Phi(b) – \Phi(a) \\
\Phi(x) &= \int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}} dz
\end{align}
$$

また、上記の左辺の分母と分子をそれぞれ$n$で割ることで、標本平均$\displaystyle \overline{X} = \frac{1}{n}(X_1+X_2+…+X_n)$に関しても下記のように表すことができる。
$$
\large
\begin{align}
\lim_{n \to \infty} P \left( a \leq \frac{(\overline{X} – \mu)}{\sigma/\sqrt{n}} \leq b \right) &= \int_{a}^{b} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx \\
&= \Phi(b) – \Phi(a) \\
\Phi(x) &= \int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}} dz
\end{align}
$$

中心極限定理の数式展開のコツと活用例

中心極限定理を用いる際のコツ

$E[S_n], V[S_n], E[\overline{X}], V[\overline{X}]$などの表記を用いる

前節で取り扱ったように、中心極限定理を用いるにあたって、考える確率変数が標本和$S_n$なのか標本平均$\overline{X}$なのかによって式の形が異なることは注意が必要である。母集団分布の母平均が$\mu$、母分散が$\sigma^2$の際に、標本和$S_n$が$\mathcal{N}(n \mu, n \sigma^2)$に従い、標本平均$\overline{X}$が$\displaystyle \mathcal{N} \left( \mu, \frac{\sigma^2}{n} \right)$に従うわけだが、二項分布では$X=S_n$で考えるなど、状況に応じて確率変数の定義の仕方が異なるのでなかなか難しい。

これに対して、標本和$S_n$は$\mathcal{N}(E[S_n], V[S_n])$に従い、標本平均$\overline{X}$が$\mathcal{N}(E[\overline{X}], V[\overline{X}])$に従うと考える方が抑えておく式の形が一つに集約できるので間違えにくいと思われる。また、母集団のパラメータは$\mu$と$\sigma^2$で定義する場合もあれば、二項分布の際のように確率を用いたり、ポアソン分布のように平均と分散のどちらも$\lambda$で表す場合など、わからなくなりやすいので、$\mathcal{N}(E[S_n], V[S_n])$のように取り扱う確率変数に対応する期待値と分散で考える方がわかりやすい。

特に母集団のパラメータは$1$つの標本に対応するパラメータであることが多い一方で、取り扱う確率変数が標本和や標本平均のように複数の標本に対応することから間違えやすいので、ここで確認したような表記の仕方の方がわかりやすいと思われる。

$\displaystyle P \left( \frac{S_n-E[S_n]}{\sqrt{V[S_n]}} \leq c \right) = P(Z \leq c) \simeq \Phi(c)$を基本形に考える

中心極限定理の適用にあたっては、式変形が複雑なこともあり、基本的な数式の形がわかりにくい場合も多いような印象を受ける。そこで、$\displaystyle P \left( \frac{S_n-E[S_n]}{\sqrt{V[S_n]}} \leq c \right) = P(Z \leq c) \simeq \Phi(c)$を基本形に考えると良いように思われる。

ここで$\Phi(z)$は標準正規分布の累積分布関数を表し、詳しくは下記のように定義できる。
$$
\large
\begin{align}
\Phi(z) = \int_{-\infty}^{z} \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx
\end{align}
$$

ここで確率変数$Z$は$S_n$に対して平均$E[S_n]$を引き、分散の平方根の$\sqrt{V[S_n]}$で割った値であることから、$Z$は$S_n$の標準化を行なった変数であると考えることができ、$Z$の平均は$0$、分散は$1$であると考えられる。よって中心極限定理に基づき、$P(Z \leq c)$が$\Phi(c)$を用いて近似を行うことができる。また、$P(Z \geq c)$には$P(Z \geq c) \simeq 1 – \Phi(c)$が対応し、$P(a \leq Z \leq b)$には$\Phi(b)-\Phi(a)$が対応することもあわせて抑えておくと良い。

・＋ α
中心極限定理は極限を考える定理だが、$P(Z \leq c) \simeq \Phi(c)$では$\to$ではなくて$\simeq$を用いた。

というのは中心極限定理はものによっては$n=20$や$n=50$の場合でも用いられることがあり、$n \to \infty$を用いて極限で考えるより$\simeq$を用いた近似で考える方が妥当であると考えられたからである。

中心極限定理の活用例

二項分布と中心極限定理

「統計学実践ワークブック」の「問$7.1$の解答例」で取り扱った。二項分布が離散型の確率分布であるので、連続型の確率分布の正規分布を用いて近似を行うにあたっては、連続修正(continuity correction)を用いて$P(X \geq 10)$を$P(X \geq 9.5)$に修正したことに着目しておくとよい。

ポアソン分布と中心極限定理

「統計学実践ワークブック」の「問$1.10$の解答例」で取り扱った。

中心極限定理の導出

中心極限定理の導出の主要な流れ

確率変数$Y_i$に関して標準化を行った確率変数を、$\displaystyle X_i = \frac{Y_i-E[Y_i]}{\sqrt{V[Y_i]}}$のように定義すると、$X_i$の平均に関して$E[X_i]=0$、分散に関して$V[X_i]=E[X_i^2]-E[X_i]^2=E[X_i^2]=1$が成立すると考えることができる。

ここで$\displaystyle \overline{X}_{n} = \frac{1}{n} \sum_{i=1}^{n} X_i$を元に下記のように$Z_n$を定める。
$$
\large
\begin{align}
Z_n &= \frac{\overline{X}_{n}-E[\overline{X}_{n}]}{\sqrt{V[\overline{X}_{n}]}} \\
&= \sqrt{n}\overline{X}_{n}
\end{align}
$$

このとき確率変数$Z_n$に関する特性関数を$\varphi_{Z_n}(t)$、確率変数$X_i$に関する特性関数を$\phi_{X_i}(t)$のように定めると、$\phi_{Z_n}(t)$は下記のように$\phi_{X_i}(t)$を用いて表すことができる。
$$
\large
\begin{align}
\phi_{Z_n}(t) &= E[e^{i t Z_n}] \\
&= E[\exp(i t \sqrt{n}\overline{X_{n}})] \\
&= E \left[ \exp \left( i t \frac{\sqrt{n}}{n} \sum_{i=1}^{n} X_i \right) \right] \\
&= E \left[ \prod_{i=1}^{n} \exp \left( i t \frac{1}{\sqrt{n}} X_i \right) \right] \\
&= E \left[ \prod_{i=1}^{n} \exp \left( i \frac{t}{\sqrt{n}} X_i \right) \right] = \left[ \phi_{X_i} \left( \frac{t}{\sqrt{n}} \right) \right]^{n} \quad (1)
\end{align}
$$

ここで$\phi_{X_i}(0), \phi_{X_i}'(0), \phi_{X_i}^{”}(0)$に関して下記が成立する。
$$
\large
\begin{align}
\phi_{X_i}(0) &= E[e^{i \cdot 0 \cdot X_i}] = E[e^{0}] = 1 \\
\phi_{X_i}'(0) &= iE[X_i] = 0 \\
\phi_{X_i}^{”}(0) &= i^2 E[X_i^2] = -1
\end{align}
$$

よって、$\varphi_{X_i}(t)$は下記のようにマクローリン展開を行うことができる。
$$
\large
\begin{align}
\phi_{X_i}(t) &= \frac{\phi_{X_i}(0)}{0!}t^{0} + \frac{\phi_{X_i}'(0)}{0!}t^{1} + \frac{\phi_{X_i}^{”}(0)}{2!}t^{2} + \cdots \\
&= 1 – \frac{t^{2}}{2} + t^{4} R(t) \quad (2)
\end{align}
$$

上記の$R(t)$は$t$の関数である。ここで$(2)$式を$(1)$式に代入することで$\phi_{Z_n}(t)$は下記のように考えることができる。
$$
\large
\begin{align}
\phi_{Z_n}(t) &= \left( 1 – \frac{t^{2}}{2n} + \frac{t^{4}}{n^2} R \left( \frac{t}{\sqrt{n}} \right) \right)^{n} \\
&= \left[ \left( 1 – \frac{t^{2}}{2n} + \frac{t^{4}}{n^2} R \left( \frac{t}{\sqrt{n}} \right) \right)^{-\frac{2n}{t^{2}}} \right]^{-\frac{t^2}{2}}
\end{align}
$$

上記に関して$t$を定数と見て$n \to \infty$を考えると、下記が成立する。
$$
\large
\begin{align}
\lim_{n \to \infty} \phi_{Z_n}(t) &= \lim_{n \to \infty} \left[ \left( 1 – \frac{t^{2}}{2n} + \frac{t^{4}}{n^2} R \left( \frac{t}{\sqrt{n}} \right) \right)^{-\frac{2n}{t^{2}}} \right]^{-\frac{t^2}{2}} \\
& \leq \lim_{n \to \infty} \left[ \left( 1 – \frac{t^{2}}{2n} + \frac{t^{4}}{n^2} c \right)^{-\frac{2n}{t^{2}}} \right]^{-\frac{t^2}{2}} \\
&= e^{-\frac{t^2}{2}} \quad (3)
\end{align}
$$

上記の導出にあたっては$t$を定数と見て$n \to \infty$を考える際に定数$c$に関して$\displaystyle R \left( \frac{t}{\sqrt{n}} \right) \leq c$が成立すると考えた。ここで定数$c$は、特性関数の導関数に関して$\phi_{X_i}^{(n)}(0)=i^{n}E[X_i^{n}]$が成立するので、実数のみを考える際は$E[X_i^{n}]$が定数であれば上限の$c$を用いて表せると考え導入を行った。$\displaystyle \frac{t^{4}}{n^2}c$の項の取り扱いでは次項で二項定理に基づいて詳しく示す。

$(3)$式が標準正規分布の特性関数に一致するので、「確率分布と特性関数の$1$対$1$対応」より、確率変数$Z_n$に関して中心極限定理が成立する。

当項の内容は「現代数理統計学」の$4.5$節を主に参考に作成を行った。

二項定理とネイピア数の定義の適用

前項の$(3)$の導出にあたっての$\displaystyle \frac{t^{4}}{n^2}c$の項の取り扱いに関して以下詳しく確認を行う。式の簡易化によって考えるにあたって、まずは$\displaystyle \lim_{n \to \infty} \left( 1 + \frac{1}{n} + \frac{1}{n^2} \right)^{n}$に関して考える。
$$
\large
\begin{align}
& \left( 1 + \frac{1}{n} + \frac{1}{n^2} \right)^{n} = \sum_{x=0}^{n} {}_{n} C_{x} \left( 1 + \frac{1}{n} \right)^{n-x} \left( \frac{1}{n^2} \right)^{x} \\
&= \left( 1 + \frac{1}{n} \right)^{n} + n \cdot \left( 1 + \frac{1}{n} \right)^{n} \cdot \frac{1}{n^2} + \frac{n(n-1)}{2} \cdot \left( 1 + \frac{1}{n} \right)^{n-2} \cdot \left( \frac{1}{n^2} \right)^{2} + \cdots
\end{align}
$$

ここで第$1$項に関して$\displaystyle \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^{n} = e$が成立するが、第$2$項以降に関しては下記のように考えることができる。

・第$2$項
$$
\large
\begin{align}
\lim_{n \to \infty} n \cdot \left( 1 + \frac{1}{n} \right)^{n} \cdot \frac{1}{n^2} &= \lim_{n \to \infty} \frac{1}{n}\left( 1 + \frac{1}{n} \right)^{n}\left( 1 + \frac{1}{n} \right)^{-1} \\
&= 0 \cdot e \cdot (1+0) \\
&= 0
\end{align}
$$

・第$3$項
$$
\large
\begin{align}
& \lim_{n \to \infty} \frac{n(n-1)}{2} \cdot \left( 1 + \frac{1}{n} \right)^{n-2} \cdot \left( \frac{1}{n^2} \right)^{2} \\
&= \lim_{n \to \infty} \frac{1 \cdot (1-1/n)}{2} \cdot \left( 1 + \frac{1}{n} \right)^{n} \left( 1 + \frac{1}{n} \right)^{-2} \cdot \frac{1}{n^2} \\
&= \frac{1}{2} \cdot e \cdot (1+0) \cdot 0 = 0
\end{align}
$$

以降の項に関しても${}_{n} C_{x}$と$\displaystyle \left( \frac{1}{n^2} \right)^{x}$の$n$の次数に着目することで$n \to \infty$を考えると$0$に収束すると考えることができる。よって下記が成立する。
$$
\large
\begin{align}
\lim_{n \to \infty} \left( 1 + \frac{1}{n} + \frac{1}{n^2} \right)^{n} = e
\end{align}
$$

同様に考えることで前項の下記の$(3)$式も導出できる。
$$
\large
\begin{align}
\lim_{n \to \infty} \left[ \left( 1 – \frac{t^{2}}{2n} + \frac{t^{4}}{n^2} c \right)^{-\frac{2n}{t^{2}}} \right]^{-\frac{t^2}{2}} = e^{-\frac{t^2}{2}} \quad (3)
\end{align}
$$

標準正規分布のモーメント母関数・特性関数

標準正規分布の確率密度関数が$\displaystyle f(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}$であるので、モーメント母関数$m_{X}(t)=E[e^{tX}]$は下記のように考えることができる。
$$
\large
\begin{align}
E[e^{tX}] &= \int_{-\infty}^{\infty} e^{tx} \times \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} dx \\
&= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} e^{-\frac{(x-t)^2}{2}} \times e^{\frac{t^2}{2}} dx \\
&= e^{\frac{t^2}{2}}
\end{align}
$$

特性関数$\phi_{X}(t)$はモーメント母関数$m_{X}(t)$を用いて$\phi_{X}(t)=m_{X}(it)$のように表せるので、標準正規分布の特性関数は下記のように考えることができる。
$$
\large
\begin{align}
\phi_{X}(t) &= m_{X}(it) \\
&= e^{\frac{(it)^2}{2}} = e^{\frac{i^2t^2}{2}} \\
&= e^{-\frac{t^2}{2}}
\end{align}
$$

確率分布と特性関数の$1$対$1$対応

反転公式(inversion formula)を元に「確率分布と特性関数の$1$対$1$対応」を考えることができる。「数理統計学(共立出版)」などが詳しい。