ブログ

当記事は「パターン認識と機械学習」の読解サポートにあたってChapter.$2$の「確率分布」の章末問題の解説について行います。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

・参考
パターン認識と機械学習 解答まとめ
https://www.hello-statisticians.com/answer_textbook_prml

解答まとめ

問題$2.21$

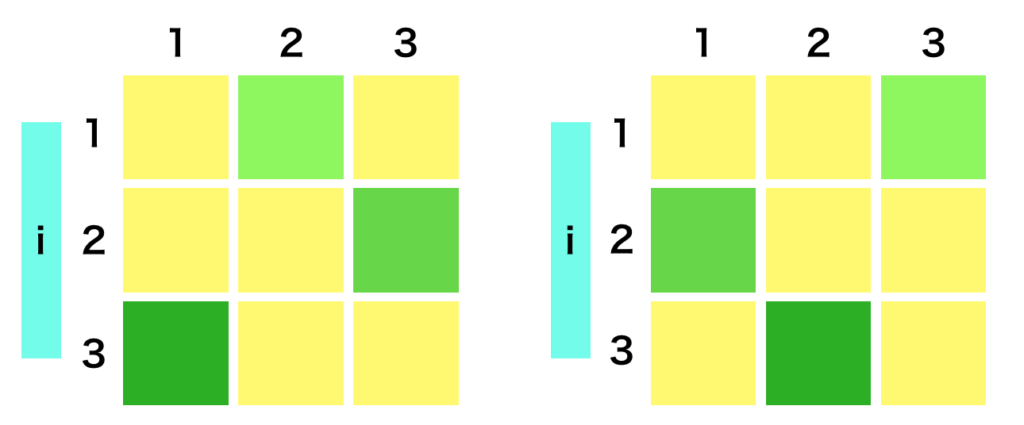
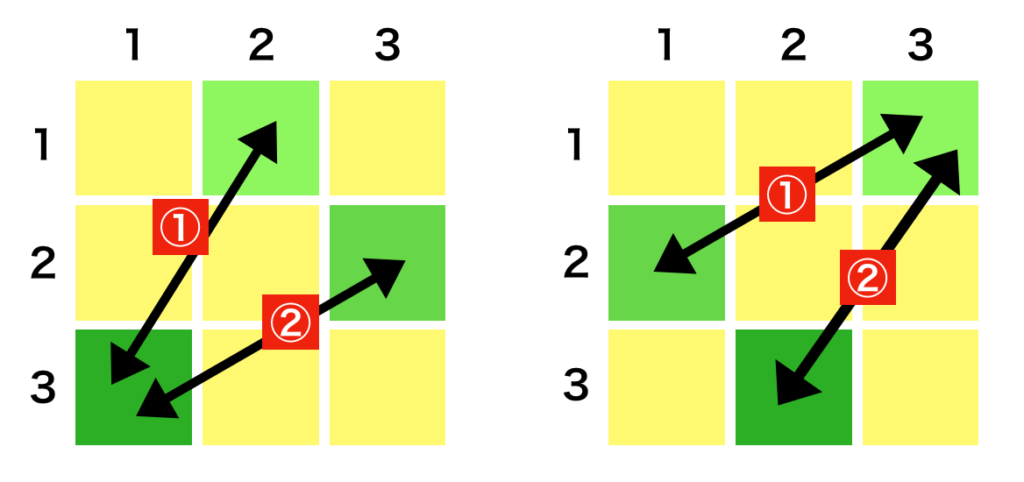
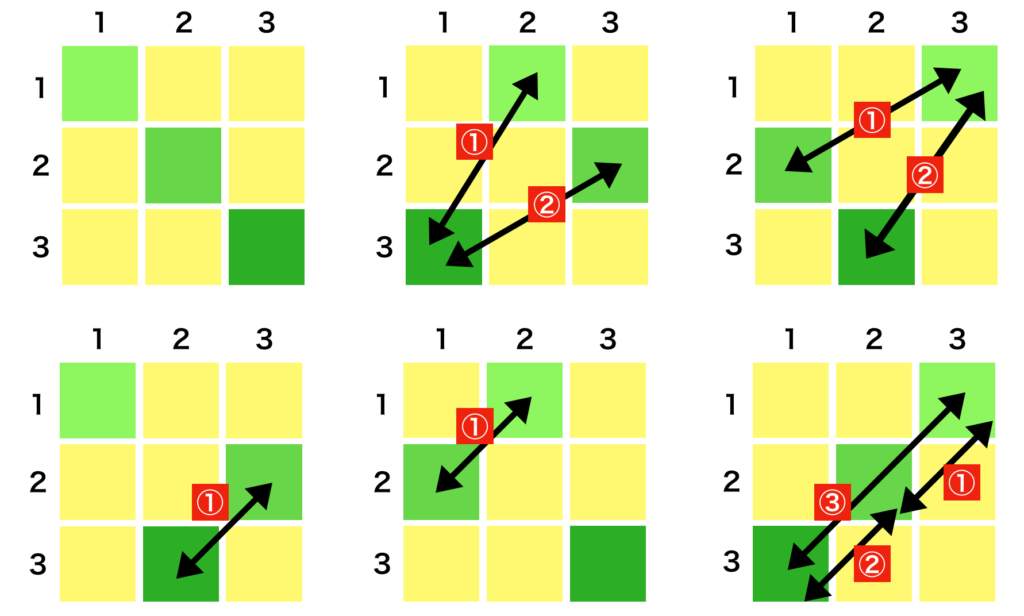
$D \times D$の対称行列を考えた際に、$(i,j)$成分と$(j,i)$成分が一致する。このことより、独立なパラメータの数は${}_D C_2$に一致するため、$\displaystyle \frac{D(D-1)}{2}$となる。

問題$2.22$

対称行列$A$を考えた際に$A$とその逆行列$A^{-1}$に関して下記が成立する。
$$
\large
\begin{align}
A A^{-1} = I
\end{align}
$$

上記の$I$は対角成分が$1$で残りの成分が$0$の単位行列である。単位行列は対称なので$I$に関して$I^{\mathrm{T}}=I$が成立する。よって、下記のように考えられる。
$$
\large
\begin{align}
(A A^{-1})^{\mathrm{T}} &= I^{\mathrm{T}} \\
(A^{-1})^{\mathrm{T}} A^{\mathrm{T}} &= I
\end{align}
$$

ここで上記の$A$も対称行列なので$A^{\mathrm{T}}=A$であり、$(A^{-1})^{\mathrm{T}} A^{\mathrm{T}} = I$はさらに下記のように変形できる。
$$
\large
\begin{align}
(A^{-1})^{\mathrm{T}} A^{\mathrm{T}} &= I \\
(A^{-1})^{\mathrm{T}} A &= I \\
(A^{-1})^{\mathrm{T}} &= A^{-1}
\end{align}
$$

上記より$A=A^{\mathrm{T}}$のとき$A^{-1}=(A^{-1})^{\mathrm{T}}$が成立するので、対称行列の逆行列は対称行列であることがわかる。

問題$2.24$

$$
\large
\begin{align}
\left(\begin{array}{cc} A & B \\ C & D \end{array} \right) &= \left(\begin{array}{cc} I_m & O \\ O^{\mathrm{T}} & I_n \end{array} \right) \quad (1) \\
M &= (A-BD^{-1}C)^{-1}
\end{align}
$$

$A,D$の次元がそれぞれ$m$次元、$n$次元であると考えるとき、$(1)$式が成立することを示す。また、上記では$m \times n$の零行列を$O$とおいた。

$$
\large
\begin{align}
& \left(\begin{array}{cc} M & -MBD^{-1} \\ -D^{-1}CM & D^{-1}+D^{-1}CMBD \end{array} \right) \left(\begin{array}{cc} A & B \\ C & D \end{array} \right) \\
&= \left(\begin{array}{cc} MA-MBD^{-1}C & MB-MB \\ -D^{-1}CMA+D^{-1}C+D^{-1}CMD^{-1}C & -D^{-1}CMB+I_n+D^{-1}CMB \end{array} \right) \\
&= \left(\begin{array}{cc} M(A-BD^{-1}C) & O \\ D^{-1}C(-MA + I +MBD^{-1}C) & I_n \end{array} \right) \\
&= \left(\begin{array}{cc} M(A-BD^{-1}C) & O \\ D^{-1}C(I_m-(A-BD^{-1}C)^{-1}(A-BD^{-1}C)) & I_n \end{array} \right) \\
&= \left(\begin{array}{cc} I_m & O \\ D^{-1}C(I_m-I_m) & I_n \end{array} \right) \\
&= \left(\begin{array}{cc} I_m & O \\ O^{\mathrm{T}} & I_n \end{array} \right) \\
\end{align}
$$

よって$(2.76)$式が成立する。

問題$2.25$

$$
\large
\begin{align}
\mathbf{\mu} = \left(\begin{array}{c} \mathbf{\mu}_{a} \\ \mathbf{\mu}_{b} \\ \mathbf{\mu}_{c} \end{array} \right), \mathbf{\Sigma} = \left(\begin{array}{ccc} \mathbf{\Sigma}_{aa} & \mathbf{\Sigma}_{ab} & \mathbf{\Sigma}_{ac} \\ \mathbf{\mu}_{ba} & \mathbf{\Sigma}_{bb} & \mathbf{\Sigma}_{bc} \\ \mathbf{\mu}_{ca} & \mathbf{\Sigma}_{cb} & \mathbf{\Sigma}_{cc} \end{array} \right) \quad (2.288)
\end{align}
$$

上記に基づいて同時分布$p(\mathbf{x}_{a},\mathbf{x}_{b},\mathbf{x}_{c})$が得られるとき、$\mathbf{x}_{c}$に関して周辺化を行なった$\displaystyle p(\mathbf{x}_{a},\mathbf{x}_{b}) = \int p(\mathbf{x}_{a},\mathbf{x}_{b},\mathbf{x}_{c}) d \mathbf{x}_{c}$の平均ベクトル$\mathbf{\mu}’$と共分散行列$\mathbf{\Sigma}’$は$(2.98)$式より下記のように考えることができる。
$$
\large
\begin{align}
\mathbf{\mu}’ &= \left(\begin{array}{c} \mathbf{\mu}_{a} \\ \mathbf{\mu}_{b} \end{array} \right) \\
\mathbf{\Sigma}’ &= \left(\begin{array}{cc} \mathbf{\Sigma}_{aa} & \mathbf{\Sigma}_{ab} \\ \mathbf{\Sigma}_{ba} & \mathbf{\Sigma}_{bb} \end{array} \right)
\end{align}
$$

次にここで得られた周辺分布$p(\mathbf{x}_{a},\mathbf{x}_{b})$に対して条件付き分布$p(\mathbf{x}_{a}|\mathbf{x}_{b})$を考える。条件付き分布の平均ベクトルを$\mathbf{\mu}_{a|b}$、共分散行列を$\mathbf{\Sigma}_{a|b}$とおくと、$(2.81),(2.82)$式より下記が得られる。
$$
\large
\begin{align}
\mathbf{\mu}_{a|b} &= \mathbf{\mu}_{a} + \mathbf{\Sigma}_{ab} \mathbf{\Sigma}_{bb}^{-1} (\mathbf{x}_{b}-\mathbf{\mu}_{b}) \\
\mathbf{\Sigma}_{a|b} &= \Sigma_{aa} – \mathbf{\Sigma}_{ab} \mathbf{\Sigma}_{bb}^{-1}\mathbf{\Sigma}_{ba}
\end{align}
$$

問題$2.26$

$$
\large
\begin{align}
(A+BCD)^{-1} = A^{-1} – A^{-1} B (C^{-1} + D A^{-1} B)^{-1} D A^{-1} \quad (2.289)
\end{align}
$$

上記の式を示すにあたって、右辺に左から$A+BCD$をかけ、下記のように変形を行う。
$$
\large
\begin{align}
& (A+BCD)(A^{-1} – A^{-1} B (C^{-1} + D A^{-1} B)^{-1} D A^{-1}) \\
&= I + BCDA^{-1} – B(C^{-1}+DA^{-1}B)^{-1}DA^{-1} – BCDA^{-1}B(C^{-1}+DA^{-1}B)^{-1}DA^{-1} \\
&= I + BCDA^{-1} – B(I+CDA^{-1}B)(C^{-1}+DA^{-1}B)^{-1}DA^{-1} \\
&= I + BCDA^{-1} – BC\cancel{(C^{-1}+DA^{-1}B)}\cancel{(C^{-1}+DA^{-1}B)^{-1}}DA^{-1} \\
&= I + BCDA^{-1} – BCDA^{-1} \\
&= I
\end{align}
$$

よって$A^{-1} – A^{-1} B (C^{-1} + D A^{-1} B)^{-1} D A^{-1}$は$A+BCD$の逆行列であると考えることができる。よってWoodbury matrix inversion formulaは成立する。

・別解
$(2.289)$式の右から$A+BCD$をかけても下記のように同様な確認を行える。
$$
\large
\begin{align}
& (A^{-1} – A^{-1} B (C^{-1} + D A^{-1} B)^{-1} D A^{-1})(A+BCD) \\
&= I + A^{-1}BCD – A^{-1} B (C^{-1} + D A^{-1} B)^{-1} D A^{-1}(A+BCD) \\
&= I + A^{-1}BCD – A^{-1} B (C^{-1} + D A^{-1} B)^{-1}(D+DA^{-1}BCD) \\
&= I + A^{-1}BCD – A^{-1} B (C^{-1} + D A^{-1} B)^{-1}(C^{-1}CD+DA^{-1}BCD) \\
&= I + A^{-1}BCD – A^{-1} B \cancel{(C^{-1} + D A^{-1} B)^{-1}}\cancel{(C^{-1}+DA^{-1}B)}CD \\
&= I + A^{-1}BCD – A^{-1}BCD = I
\end{align}
$$

なお巻末のAppendix.Cでは$(2.289)$の$C$を$D^{-1}$、$D$を$C$で置き換えて下記のような式でWoodbury matrix inversion formulaを表すことに注意しておくとよい。
$$
\large
\begin{align}
(A+BD^{-1}C)^{-1} = A^{-1} – A^{-1} B (D + C A^{-1} B)^{-1} C A^{-1} \quad (C.7)
\end{align}
$$

問題$2.29$

$$
\large
\begin{align}
R = \left(\begin{array}{cc} \Lambda+A^{\mathrm{T}}LA & -A^{\mathrm{T}}L \\ -LA & L \end{array} \right) \quad (2.104)
\end{align}
$$

上記のように表される$(2.104)$式に$(2.76)$式を用いるにあたって、先に$M = (\Lambda+A^{\mathrm{T}}LA – (-A^{\mathrm{T}}L) L^{-1} (-LA))^{-1}$の計算を行う。
$$
\large
\begin{align}
M &= (\Lambda + A^{\mathrm{T}}LA – (-A^{\mathrm{T}}L) L^{-1} (-LA))^{-1} \\
&= (\Lambda + A^{\mathrm{T}}LA – A^{\mathrm{T}}LA)^{-1} \\
&= \Lambda^{-1}
\end{align}
$$

よって$R^{-1}$は下記のようにを導出することができる。
$$
\large
\begin{align}
R^{-1} &= \left(\begin{array}{cc} \Lambda+A^{\mathrm{T}}LA & -A^{\mathrm{T}}L \\ -LA & L \end{array} \right)^{-1} \\
&= \left(\begin{array}{cc} M & -M(-A^{\mathrm{T}}L)L^{-1} \\ L^{-1}(-LA)M & L^{-1}+L^{-1}(-LA)M(-A^{\mathrm{T}}L)L^{-1} \end{array} \right) \\
&= \left(\begin{array}{cc} M & MA^{\mathrm{T}} \\ AM & L^{-1}+AMA^{\mathrm{T}} \end{array} \right) = \left(\begin{array}{cc} \Lambda^{-1} & \Lambda^{-1}A^{\mathrm{T}} \\ A\Lambda^{-1} & L^{-1}+A\Lambda^{-1}A^{\mathrm{T}} \end{array} \right) \quad (2.105)
\end{align}
$$

上記より$(2.105)$式が成立することが示される。

問題$2.30$

$$
\large
\begin{align}
\mathbb{E}[z] &= R^{-1} \left(\begin{array}{c} \Lambda \mu – A^{\mathrm{T}}Lb \\ Lb \end{array} \right) \quad (2.107) \\
R^{-1} &= \left(\begin{array}{cc} \Lambda^{-1} & \Lambda^{-1}A^{\mathrm{T}} \\ A\Lambda^{-1} & L^{-1}+A\Lambda^{-1}A^{\mathrm{T}} \end{array} \right) \quad (2.105)
\end{align}
$$

$(2.107)$式に$(2.105)$式を代入し、$(2.108)$式の導出を行う。
$$
\large
\begin{align}
\mathbb{E}[z] &= R^{-1} \left(\begin{array}{c} \Lambda \mu – A^{\mathrm{T}}Lb \\ Lb \end{array} \right) \quad (2.107) \\
&= \left(\begin{array}{cc} \Lambda^{-1} & \Lambda^{-1}A^{\mathrm{T}} \\ A\Lambda^{-1} & L^{-1}+A\Lambda^{-1}A^{\mathrm{T}} \end{array} \right) \left(\begin{array}{c} \Lambda \mu – A^{\mathrm{T}}Lb \\ Lb \end{array} \right) \\
&= \left(\begin{array}{c} \Lambda \mu – \Lambda^{-1}A^{\mathrm{T}}Lb + \Lambda^{-1}A^{\mathrm{T}}Lb \\ A \mu – A \Lambda^{-1}A^{\mathrm{T}}Lb + b + A \Lambda^{-1}A^{\mathrm{T}}Lb \end{array} \right) = \left(\begin{array}{c} \Lambda \mu \\ A \mu + b \end{array} \right) \quad (2.108)
\end{align}
$$

上記より$(2.108)$式は成立する。

問題$2.34$

$$
\large
\begin{align}
\ln{p(\mathbf{X}|\mathbf{\mu},\Sigma)} = – \frac{ND}{2} \ln{(2 \pi)} – \frac{N}{2} \ln{|\Sigma|} – \frac{1}{2} \sum_{n=1}^{N} (\mathbf{x}_{n}-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_{n}-\mu) \quad (2.118)
\end{align}
$$

上記のように表される$(2.118)$式を$\mu = \mu_{ML}$のとき$\Sigma$に関して最大化することを考える。
$$
\large
\begin{align}
\frac{\partial}{\partial \Sigma} \ln{p(\mathbf{X}|\mathbf{\mu},\Sigma)} = – \frac{N}{2} \frac{\partial}{\partial \Sigma} \ln{|\Sigma|} – \frac{1}{2} \frac{\partial}{\partial \Sigma} \sum_{n=1}^{N} (\mathbf{x}_{n}-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_{n}-\mu) \quad (1)
\end{align}
$$

$(1)$式の第$1$項は$(C.28)$式より下記となる。
$$
\large
\begin{align}
– \frac{N}{2} \frac{\partial}{\partial \Sigma} \ln{|\Sigma|} &= – \frac{N}{2}(\Sigma^{-1})^{\mathrm{T}} \\
&= – \frac{N}{2} \Sigma^{-1}
\end{align}
$$

また、$(1)$式の第$2$項を$\Sigma$で微分するにあたって下記のように書き換えを行う。
$$
\large
\begin{align}
\sum_{n=1}^{N} (\mathbf{x}_{n}-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_{n}-\mu) &= \sum_{n=1}^{N} (\mathbf{x}_{n}-\mu)^{\mathrm{T}} \Lambda (\mathbf{x}_{n}-\mu) \\
&= \sum_{n=1}^{N} \sum_{i=1}^{D} \sum_{j=1}^{D} \lambda_{ij} (\mathbf{x}_{n}-\mu)_{i} (\mathbf{x}_{n}-\mu)_{j} \\
&= N \mathrm{Tr} \left[ \Sigma^{-1} S \right] \\
\Lambda &= \Sigma^{-1} \\
S &= \frac{1}{N} \sum_{n=1}^{N} (\mathbf{x}_{n}-\mu_{ML}) (\mathbf{x}_{n}-\mu_{ML})^{\mathrm{T}}
\end{align}
$$

ここで$\Sigma$の$(i,j)$成分を$\Sigma_{ij}$とおくと、$(1)$式の第$2$項の$\Sigma$に関する部分の$\Sigma_{ij}$での微分は下記のように考えられる。
$$
\large
\begin{align}
\frac{\partial}{\partial \Sigma_{ij}} \sum_{n=1}^{N} (\mathbf{x}_{n}-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_{n}-\mu) &= N \frac{\partial}{\partial \Sigma_{ij}} \mathrm{Tr} \left[ \Sigma^{-1} S \right] \\
&= N \mathrm{Tr} \left[ \frac{\partial}{\partial \Sigma_{ij}} \Sigma^{-1} S \right] \\
&= N \mathrm{Tr} \left[ – \Sigma^{-1} \frac{\partial \Sigma}{\partial \Sigma_{ij}} \Sigma^{-1} S \right] \quad (C.21) \\
&= N \mathrm{Tr} \left[ – \frac{\partial \Sigma}{\partial \Sigma_{ij}} \Sigma^{-1} S \Sigma^{-1} \right] \quad (C.9) \\
&= – N \left( \Sigma^{-1} S \Sigma^{-1} \right)_{ij}
\end{align}
$$

よって$(1)$式の第$2$項の$\Sigma$での微分は下記のように考えられる。
$$
\large
\begin{align}
-\frac{1}{2} \frac{\partial}{\partial \Sigma} \sum_{n=1}^{N} (\mathbf{x}_{n}-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_{n}-\mu) = \frac{N}{2} \Sigma^{-1} S \Sigma^{-1}
\end{align}
$$

$(2)$式、$(3)$式より、$(2.118)$式を最大にする$\Sigma$は下記のように計算できる。
$$
\large
\begin{align}
– \frac{N}{2} \Sigma^{-1} + \frac{N}{2} \Sigma^{-1} S \Sigma^{-1} &= 0 \\
\frac{N}{2} \Sigma^{-1} &= \frac{N}{2} \Sigma^{-1} S \Sigma^{-1} \\
\Sigma^{-1} &= S = \frac{1}{N} \sum_{n=1}^{N} (\mathbf{x}_{n}-\mu_{ML}) (\mathbf{x}_{n}-\mu_{ML})^{\mathrm{T}}
\end{align}
$$

問題$2.36$

サンプル$N$に対応する$\sigma_{ML}^{2}$を$\sigma_{(N)}^{2}$のようにおく。このとき$(2.292)$式に対して$(2.126)$式と同様の変形を考える。
$$
\large
\begin{align}
\sigma_{(N)}^{2} &= \frac{1}{N} \sum_{i=1}^{N} (x_n-\mu)^{2} \\
&= \frac{1}{N} (x_N-\mu)^{2} + \frac{1}{N} \sum_{i=1}^{N-1} (x_n-\mu)^{2} \\
&= \frac{1}{N} (x_N-\mu)^{2} + \frac{N-1}{N} \times \frac{1}{N-1} \sum_{i=1}^{N-1} (x_n-\mu)^{2} \\
&= \frac{N-1}{N} \sigma_{(N-1)}^{2} + \frac{1}{N} (x_N-\mu)^{2} \\
&= \sigma_{(N-1)}^{2} + \frac{1}{N} \left[ (x_N-\mu)^{2} – \sigma_{(N-1)}^{2} \right] \quad (1)
\end{align}
$$

また、$\sigma_{(N)}^{2} = \tau_{(N)}$のようにおき、Robbins-Monroの式を適用することを考える。
$$
\large
\begin{align}
\tau_{(N)} &= \tau_{(N-1)} + a_{N-1} \frac{\partial}{\partial \tau_{(N)}} \ln{p(x_{N}|\tau_{(N-1)})} \\
&= \tau_{(N-1)} + a_{N-1} \frac{\partial}{\partial \tau_{(N)}} \left[ – \frac{(x_N-\mu)^2}{2 \tau_{(N-1)}} – \frac{1}{2} \ln{\tau_{N-1}} + \mathrm{Const.} \right] \\
&= \tau_{(N-1)} + a_{N-1} \left[ \frac{(x_N-\mu)^2}{2 \tau_{(N-1)}^2} – \frac{1}{2 \tau_{N-1}} \right] \\
&= \tau_{(N-1)} + \frac{a_{N-1}}{2 \tau_{(N-1)}^2} \left[ (x_N-\mu)^2 – \tau_{N-1} \right] \\
&= \sigma_{(N-1)}^{2} + \frac{a_{N-1}}{2 \sigma_{(N-1)}^4} \left[ (x_N-\mu)^2 – \sigma_{N-1}^2 \right] \quad (2)
\end{align}
$$

$(1)$式と$(2)$式より$\displaystyle \frac{a_{N-1}}{2 \sigma_{(N-1)}^4} = \frac{1}{N}$が成立し、これより$\displaystyle a_{N-1} = \frac{2 \sigma_{(N-1)}^4}{N}$であることがわかる。

問題$2.38$

$(2.137)$〜$(2.140)$式より、事後分布$\mathcal{N}(\mu|\mu_{N},\sigma_{N}^{2})$を下記のように考えることができる。
$$
\large
\begin{align}
\mathcal{N}(\mu|\mu_{N},\sigma_{N}^{2}) &= p(\mu|x_1,x_2,…,x_N) \\
& \propto p(x_1,x_2,…,x_N|\mu)p(\mu) \\
& \propto \exp \left( – \frac{1}{2 \sigma^2} \sum_{n=1}^{N}(x_n-\mu)^2 \right) \times \exp \left( – \frac{(\mu-\mu_{0})^2}{2 \sigma_{0}^{2}} \right) \\
&= \exp \left( – \frac{1}{2 \sigma^2} \sum_{n=1}^{N}(\mu^2 – 2x_n \mu + x_n^2) – \frac{(\mu-\mu_{0})^2}{2 \sigma_{0}^{2}} \right) \\
&= \exp \left[ – \frac{1}{2 \sigma^2} \left( N \mu^2 – 2 N \mu_{ML} \mu + \sum_{n=1}^{N} x_n^2 \right) – \frac{(\mu-\mu_{0})^2}{2 \sigma_{0}^{2}} \right]
\end{align}
$$

上記の指数関数の内部を$\mu$に関して平方完成することを考えると、下記のように変形を行うことができる。
$$
\large
\begin{align}
& – \frac{1}{2 \sigma^2} \left( N \mu^2 – 2 N \mu_{ML} \mu + \sum_{n=1}^{N} x_n^2 \right) – \frac{(\mu-\mu_{0})^2}{2 \sigma_{0}^{2}} \\
&= – \frac{N \mu^2 – 2 N \mu_{ML} \mu}{2 \sigma^2} – \frac{\mu^2 – 2\mu_{0} \mu}{2 \sigma_{0}^{2}} + \mathrm{Const.} \\
&= – \frac{1}{2 \sigma^2 \sigma_{0}^{2}} \left( N \sigma_{0}^{2} \mu^2 – 2 N \sigma_{0}^{2} \mu_{ML} \mu + \sigma^2 \mu^2 – 2 \sigma^2 \mu_{0} \mu \right) + \mathrm{Const.} \\
&= – \frac{1}{2 \sigma^2 \sigma_{0}^{2}} \left( (N \sigma_{0}^{2} + \sigma^2) \mu^2 – 2 (N \sigma_{0}^{2} \mu_{ML} + \sigma^2 \mu_{0}) \mu \right) + \mathrm{Const.} \\
&= – \frac{N \sigma_{0}^{2} + \sigma^2}{2 \sigma^2 \sigma_{0}^{2}} \left( \mu – \frac{N \sigma_{0}^{2} \mu_{ML} + \sigma^2 \mu_{0}}{N \sigma_{0}^{2} + \sigma^2} \right) + \mathrm{Const’.}
\end{align}
$$

上記より$\mu_{N}, \sigma_{N}^{2}$は下記が対応することがわかる。
$$
\large
\begin{align}
\mu_{N} &= \frac{N \sigma_{0}^{2} \mu_{ML} + \sigma^2 \mu_{0}}{N \sigma_{0}^{2} + \sigma^2} \\
&= \frac{\sigma^2}{N \sigma_{0}^{2} + \sigma^2} \mu_{0} + \frac{N \sigma_{0}^{2}}{N \sigma_{0}^{2} + \sigma^2} \mu_{ML} \\
\frac{1}{\sigma_{N}^{2}} &= \frac{N \sigma_{0}^{2} + \sigma^2}{\sigma^2 \sigma_{0}^{2}} = \frac{1}{\sigma_{0}^{2}} + \frac{N}{\sigma^2}
\end{align}
$$

よって$(2.141)$式、$(2.142)$式が成立することが示される。

・参考
統計検定準$1$級 ベイズ法と事後分布の出題

問題$2.40$

$$
\large
\begin{align}
p(\mu) &= \mathcal{N}(\mu|\mu_{0},\Sigma_{0}) = \frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma_{0}|^{1/2}} \exp \left[ -\frac{1}{2} (\mu-\mu_{0})^{\mathrm{T}} \Sigma_{0}^{-1} (\mu-\mu_{0}) \right] \quad (1) \\
p(\mathbf{x}_1,…,\mathbf{x}_N|\mu) &= \prod_{n=1}^{N} p(\mathbf{x}_n|\mu) = \prod_{n=1}^{N} \frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} \exp \left[ -\frac{1}{2} (\mathbf{x}_n-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_n-\mu) \right] \quad (2)
\end{align}
$$

上記の$(1)$式$(2)$式より、事後分布$p(\mu|\mathbf{X}) = p(\mu|\mathbf{x}_1,…,\mathbf{x}_N)$は$\mu$を変数と見る際に下記のように考えられる。
$$
\large
\begin{align}
p(\mu|\mathbf{X}) &= p(\mu|\mathbf{x}_1,…,\mathbf{x}_N) \\
& \propto p(\mathbf{x}_1,…,\mathbf{x}_N|\mu) p(\mu) \\
& \propto \exp \left[ -\frac{1}{2} (\mu-\mu_{0})^{\mathrm{T}} \Sigma_{0}^{-1} (\mu-\mu_{0}) \right] \times \exp \left[ – \frac{1}{2} \sum_{n=1}^{N} (\mathbf{x}_n-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_n-\mu) \right] \\
&= \exp \left[ – \frac{1}{2} (\mu-\mu_{0})^{\mathrm{T}} \Sigma_{0}^{-1} (\mu-\mu_{0}) – \frac{1}{2} \sum_{n=1}^{N}(\mathbf{x}_n-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}_n-\mu) \right] \\
& \propto \exp \left[ -\frac{1}{2} \mu^{\mathrm{T}} \left( \Sigma_{0}^{-1} + N \Sigma^{-1} \right) \mu + \mu^{\mathrm{T}} \left( \Sigma_{0}^{-1} \mu_{0} + \Sigma^{-1} \sum_{n=1}^{N} \mathbf{x}_n \right) \right] \quad (3)
\end{align}
$$

上記の$\exp$の内部を平方完成するにあたっては、$(3)$式と下記の$(2.71)$式との対応を確認すればよい。
$$
\large
\begin{align}
– \frac{1}{2} (\mathbf{x}-\mu)^{\mathrm{T}} \Sigma^{-1} (\mathbf{x}-\mu) = – \frac{1}{2} \mathbf{x}^{\mathrm{T}} \Sigma^{-1} \mathbf{x} + \mathbf{x}^{\mathrm{T}} \Sigma^{-1} \mu + \mathrm{Const.} \quad (2.71)
\end{align}
$$

事後分布の平均ベクトルを$\mu_{N}$、共分散行列を$\Sigma_{N}$とおくと、$\mu_{N}, \Sigma_{N}^{-1}$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
\Sigma_{N}^{-1} &= \Sigma_{0}^{-1} + N \Sigma^{-1} \\
\Sigma_{N}^{-1} \mu_{N} &= \left( \Sigma_{0}^{-1} \mu_{0} + \Sigma^{-1} \sum_{n=1}^{N} \mathbf{x}_n \right) \\
\mu_{N} &= \Sigma_{N} \left( \Sigma_{0}^{-1} \mu_{0} + \Sigma^{-1} N \mu_{ML} \right) \\
&= \left( \Sigma_{0}^{-1} + N \Sigma^{-1} \right)^{-1} \left( \Sigma_{0}^{-1} \mu_{0} + \Sigma^{-1} N \mu_{ML} \right) \\
\mu_{ML} &= \frac{1}{N} \sum_{n=1}^{N} \mathbf{x}_n
\end{align}
$$