「統計学実践ワークブック」 演習問題etc Ch.25 「因子分析・グラフィカルモデル」

当記事は「統計学実践ワークブック(学術図書出版社)」の読解サポートにあたってChapter.25の「主成分分析」に関して演習問題を中心に解説を行います。実際の分析にあたって用いられる場合がある手法なので、演習を通して抑えておくと良いと思われました。

本章のまとめ

$1$因子の因子分析(factor analysis)

因子分析(factor analysis)は$p$個の変数によって表される現象を少数の共通要因によって単純化を行う手法である。このとき、共通の要因を共通因子(common factor)と呼ぶ。

数学の試験を例に以下具体的に考える。生徒$i$の問$j$における得点を$x_{ij}$とおく。このとき$x_{ij}$を生徒$i$の因子スコア$f_i \sim N(0,1)$などを元に下記のように考えられると仮定する。
$$
\large
\begin{align}
x_{ij} = a_j f_{i} + d_j u_{ij}
\end{align}
$$
上記は$x_{ij}$が$1$つの共通因子$f_i$の関数で表されることから、$1$因子モデル(single factor model)と言われる。

ここで「共通因子$f_i$と各問$j$の関係を表す係数$a_j$」は「因子負荷量(factor loading)」と呼ばれ、共通因子では説明できない部分の$d_j u_{ij}$に関しては$d_j$を独自係数(coefficient unique factor)、$u_{ij}$を独自性因子(unique factor)と呼ぶ。

また、$x_{ij}$に関しては$V[x_{ij}]=a_j^2+d_j^2$が成立し、$a_j^2$を問$j$の共通性(communality)、$d_j^2$を問$j$の独自性(uniqueness)ということも抑えておくと良い。

実際に用いるにあたっては観測可能なのが$x_{ij}$だけであるので、$a_j, f_{i}, d_j, u_{ij}$はそれぞれ最尤推定などを用いて推定を行う。

多因子の因子分析

一般に共通因子が$K$個の場合は$K$因子モデルと言われ、下記のように表される。
$$
\large
\begin{align}
x_{ij} = a_{j1} f_{i1} + a_{j2} f_{i2} + … + a_{jK} f_{iK} + d_j u_{ij}
\end{align}
$$

多因子の因子分析を行うにあたっては、因子負荷量$a_{jk}$に関する行列の因子負荷行列の見方を抑えておくと良い。

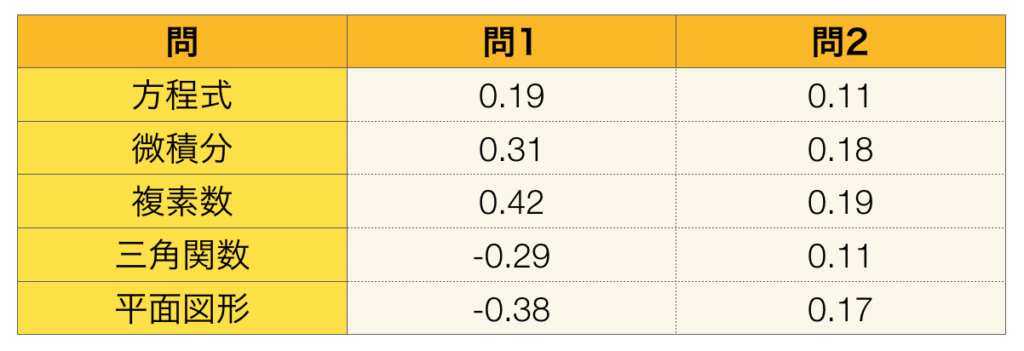
上記のような推定値が得られたとき、「方程式」、「微積分」、「複素数」は問1と問2のどちらの因子負荷量も大きいが、「三角関数」と「平面図形」は問1に対応する因子負荷量がマイナスである一方で問2の因子負荷量がプラスであることが確認できる。

これにより、因子の効果を考察することができるが、このままだとわかりにくいので回転を考えることで解釈を行いやすくする手法がある。

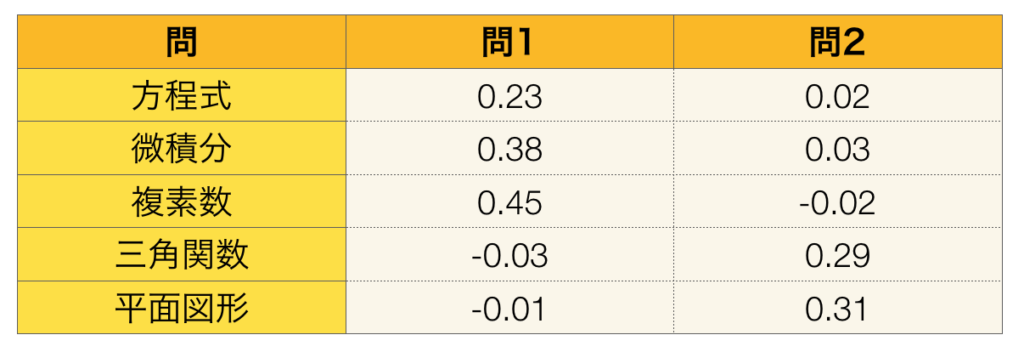
たとえば上記のように変換を行えば第$1$因子で「方程式」、「微積分」、「複素数」、第$2$因子で「三角関数」と「平面図形」をそれぞれ考慮すれば良いことから解釈が行いやすい。このときに行う手続きを回転(rotation)という。

回転に関しては、主に「バリマックス法(varimax rotation)」などの「直交回転(orghogonal rotation)」や、直交しない回転である「斜交回転(oblique rotation)」などの考え方があることを抑えておくと良い。

構造方程式(Stractural equation)

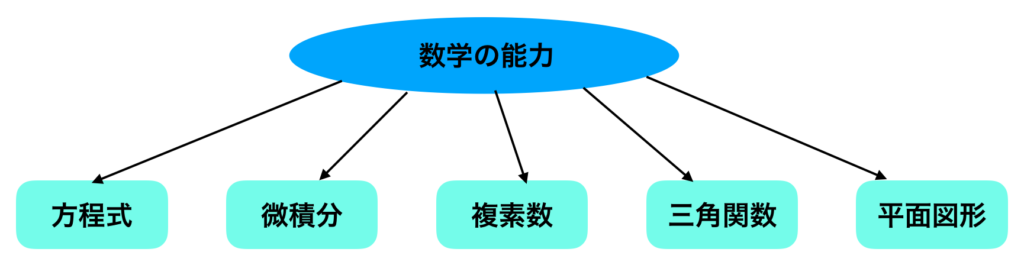
$1$因子モデルは上記のように表すこともできるが、上記のような有向グラフに基づいて考えるモデルを構造方程式モデル(Stractural equation model)という。よって、「因子分析モデル」は「構造方程式モデル」の一種であると考えることができる。

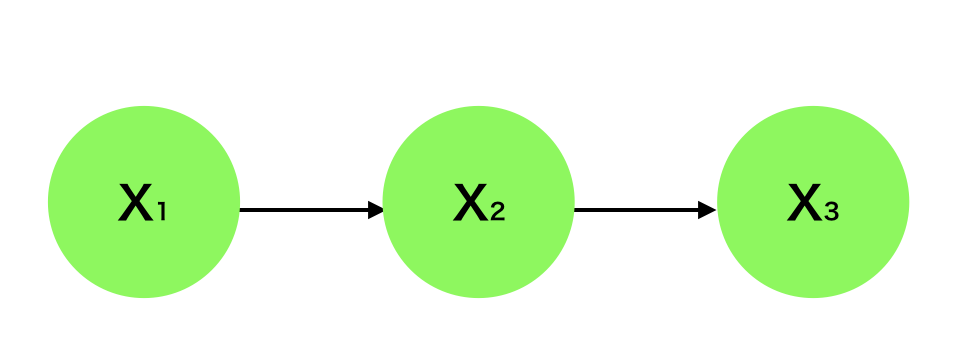
より具体的に考えるにあたって、上記を元に下記のような数式を考える。
$$
\large
\begin{align}
X_{2} &= a X_{1} + u \\
X_{3} &= b X_{2} + v \\
X_{1}, &X_{2}, X_{3} \sim N(0,1)
\end{align}
$$
上記の$u, v$は誤差項であり、$u$は$X_1$と$v$は$X_1, X_2$とそれぞれ無相関であると仮定する。また、回帰係数$a, b$はそれぞれパス係数(path coefficient)と呼ばれる。

ここで$1$式目の両辺に$X_1$を掛け、期待値を取ることで下記のような導出を行うことができる。
$$
\large
\begin{align}
\rho_{12} &= Cov(X_1,X_2) \\
X_{2} &= a X_{1} + u \\
X_{1} X_{2} &= a X_{1}^2 + u X_1 \\
E[X_{1} X_{2}] &= E[a X_{1}^2 + u X_1] \\
\rho_{12} &= aE[X_{1}^2] + u E[X_1] \\
&= a \\
a &= \rho_{12}
\end{align}
$$

上記では$X_1$と$X_2$の共分散を$\rho_{12}$とおいた。また、同様に$2$式目の両辺に$X_2$を掛け、期待値を取ることで下記のような導出を行うことができる。
$$
\large
\begin{align}
\rho_{23} &= Cov(X_2,X_3) \\
X_{3} &= b X_{2} + v \\
X_{2} X_{3} &= b X_{2}^2 + b X_2 \\
E[X_{2} X_{3}] &= E[b X_{2}^2 + b X_2] \\
\rho_{23} &= bE[X_{2}^2] + u E[X_2] \\
&= b \\
b &= \rho_{23}
\end{align}
$$

このようなパス係数$a, b$の導出の方法は操作変数法(instrumental variable method)と呼ばれ、様々な構造方程式に適用することができる。また、ここで確認した操作変数法の手続きは最小二乗法と等価であることも抑えておくと良い。

演習問題解説

例25.1

$[1]$
全ての因子負荷量が正であることから、共通因子は「数学の能力の高さ」と考えることができる。

$[2]$
方程式の共通性を$a_1^2$、独自性を$d_1^2$とおくと、$a_1^2+d_1^2=1$より、それぞれ下記のように計算できる。
$$
\large
\begin{align}
a_1^2 &= 0.92^2 = 0.8464 \\
d_1^2 &= 1-a_1^2 = 1-0.8464 \\
&= 0.1536
\end{align}
$$

$[3]$
因子スコアは成績の良い順と考えられるので、下記のような対応であると考えられる。

A: -1.613
B: 1.462
C: 0.193

例25.2

$$
\large
\begin{align}
X_3 = b X_2 + v
\end{align}
$$

上記で表した$(25.2)$の第$2$式に対して両辺に$X_1$をかけて、両辺の期待値を取ることで下記のように計算できる。
$$
\large
\begin{align}
E[X_3X_1] &= E[(b X_2 + v)X_1] \\
\rho_{31} &= b E[X_1X_2] + E[v]E[X_1] = b \rho_{12} \\
b &= \frac{\rho_{31}}{\rho_{12}}
\end{align}
$$

問25.1

$[1]$
因子負荷量の絶対値$|a_{12}|$は下記のように計算できる。
$$
\large
\begin{align}
|a_{12}| &= \sqrt{0.8545-(-0.92)^2} \\
&= 0.09
\end{align}
$$

$[2]$
因子$1$のスコアが小さく、因子$2$のスコアが大きいものを選べば良いのでJが適切であることがわかる。

問25.2

$[1]$
$$
\large
\begin{align}
Y &= aX + bW + u \quad (1) \\
Z &= cX + dY + v \quad (2)
\end{align}
$$

上記の$(1)$式の両辺に$X$をかけて期待値を取ると下記のように変形を行うことができる。
$$
\large
\begin{align}
Y &= aX + bW + u \\
XY &= aX^2 + bXW + uX \\
E[XY] &= aE[X^2] + bE[XW] + E[uX] \\
\rho_{xy} &= a \cdot 1 \\
a &= \rho_{xy}
\end{align}
$$

同様に$(1)$式の両辺に$W$をかけて期待値を取ると下記のように変形を行うことができる。
$$
\large
\begin{align}
Y &= aX + bW + u \\
YW &= aXW + bW^2 + uW \\
E[YW] &= aE[XW] + bE[W^2] + E[uW] \\
\rho_{yw} &= b \cdot 1 \\
b &= \rho_{yw}
\end{align}
$$

次に$(2)$式の両辺に$X, Y$をそれぞれかけて期待値を取るとそれぞれ下記のように変形できる。
$$
\large
\begin{align}
Z &= cX + dY + v \\
XZ &= cX^2 + dXY + vX \\
E[XZ] &= cE[X^2] + dE[XY] + E[vX] \\
\rho_{xz} &= c \cdot 1 + d \rho_{xy} + 0 \\
\rho_{xz} &= c + d \rho_{xy} \quad (2.1)
\end{align}
$$
$$
\large
\begin{align}
Z &= cX + dY + v \\
YZ &= cXY + dY^2 + vY \\
E[YZ] &= cE[XY] + dE[Y^2] + vY \\
\rho_{yz} &= c \rho_{xy} + d \cdot 1 + 0 \\
\rho_{yz} &= c \rho_{xy} + d \quad (2.2)
\end{align}
$$

$(2.1)$式と$(2.2)$式に関する連立方程式を解くと、$c, d$は下記のように計算することができる。
$$
\large
\begin{align}
c &= \frac{\rho_{xz}-\rho_{xy}\rho_{yz}}{1-\rho_{xy}^2} \\
d &= \frac{\rho_{yz}-\rho_{xy}\rho_{xz}}{1-\rho_{xy}^2}
\end{align}
$$

$[2]$
$[1]$の結果より$c+ad$は下記のように計算できる。
$$
\large
\begin{align}
c + ad &= \frac{\rho_{xz}-\rho_{xy}\rho_{yz}}{1-\rho_{xy}^2} + \rho_{xy} \frac{\rho_{yz}-\rho_{xy}\rho_{xz}}{1-\rho_{xy}^2} \\
&= \frac{\rho_{xz}(1-\rho_{xy}^2)}{1-\rho_{xy}^2} \\
&= \rho_{xz}
\end{align}
$$

上記より$\rho_{xz} = c + ad$を示すことができる。

$[3]$
モラルグラフは定義より下記のように描くことができる。

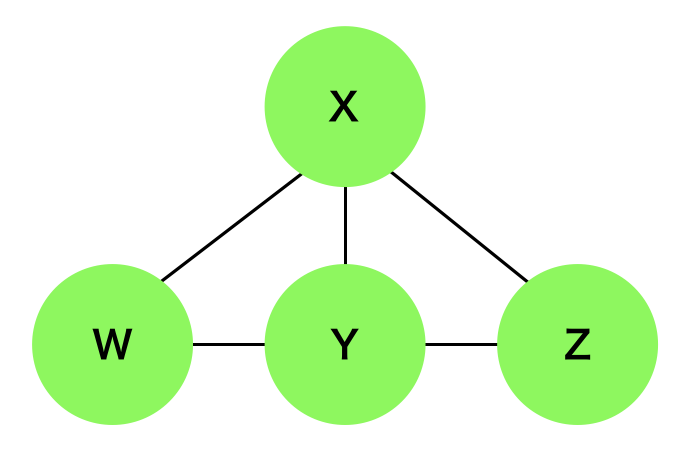
参考

・準1級関連まとめ
https://www.hello-statisticians.com/toukeikentei-semi1