当記事は「パターン認識と機械学習」の読解サポートにあたってChapter.2の「確率分布」の章末問題の解説について行います。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。
・参考
パターン認識と機械学習 解答まとめ
解答まとめ
問題2.41
$$
\begin{align}
Gamma(\lambda|a,b) = \frac{b^a}{\Gamma(a)} \lambda^{a-1} e^{-b \lambda}
\end{align}
$$
上記のように定義されるガンマ分布に対して、$0 \leq \lambda \leq \infty$の区間で積分を行う。
$$
\begin{align}
\int_{0}^{\infty} Gamma(\lambda|a,b) d \lambda &= \frac{b^a}{\Gamma(a)} \int_{0}^{\infty} \lambda^{a-1} e^{-b \lambda} d \lambda
\end{align}
$$
上記において、$(1.141)$式を参考に$u = b \lambda$のように置き換えることを考える。このとき$d \lambda = b^{-1} du$のように置き換えることができる。
$$
\begin{align}
\int_{0}^{\infty} Gamma(\lambda|a,b) d \lambda &= \frac{b^a}{\Gamma(a)} \int_{0}^{\infty} \lambda^{a-1} e^{-b \lambda} d \lambda \\
&= \frac{b^a}{\Gamma(a)} \int_{0}^{\infty} \left(\frac{u}{b}\right)^{a-1} e^{-u} b^{-1} du \\
&= \frac{1}{\Gamma(a)} \int_{0}^{\infty} u^{a-1} e^{-u} du
\end{align}
$$
ガンマ関数の定義より、$\displaystyle \Gamma(a) = \int_{0}^{\infty} u^{a-1} e^{-u} du$が成立するので、$\displaystyle \int_{0}^{\infty} Gamma(\lambda|a,b) d \lambda=1$となり、これはガンマ分布が正規化されていることを表す。
問題2.42
期待値を$E[\lambda]$、分散を$V[\lambda]$とした際に、それぞれ下記のような数式で定義される。
$$
\begin{align}
E[\lambda] &= \int_{0}^{\infty} \lambda Gamma(\lambda|a,b) d \lambda \\
V[\lambda] &= \int_{0}^{\infty} (\lambda-E[\lambda])^2 Gamma(\lambda|a,b) d \lambda
\end{align}
$$
以下、それぞれの式について計算する。
期待値$E[\lambda]$は下記のように計算することができる。
$$
\begin{align}
E[\lambda] &= \int_{0}^{\infty} \lambda Gamma(\lambda|a,b) d \lambda \\
&= \frac{b^a}{\Gamma(a)} \int_{0}^{\infty} \lambda^{a} e^{-b \lambda} d \lambda \\
&= \frac{b^a}{\Gamma(a)} \left[ -\lambda^{a} b^{-1} e^{-b \lambda} \right]_{0}^{\infty} + \frac{b^a}{\Gamma(a)} \int_{0}^{\infty} a b^{-1} \lambda^{a-1} e^{-b \lambda} d \lambda \\
&= \frac{1}{\Gamma(a)} \Gamma(a) a b^{-1} \\
&= \frac{a}{b}
\end{align}
$$
途中の計算では問題$2.41$の結果を利用した。
問題$2.43$
$$
\large
\begin{align}
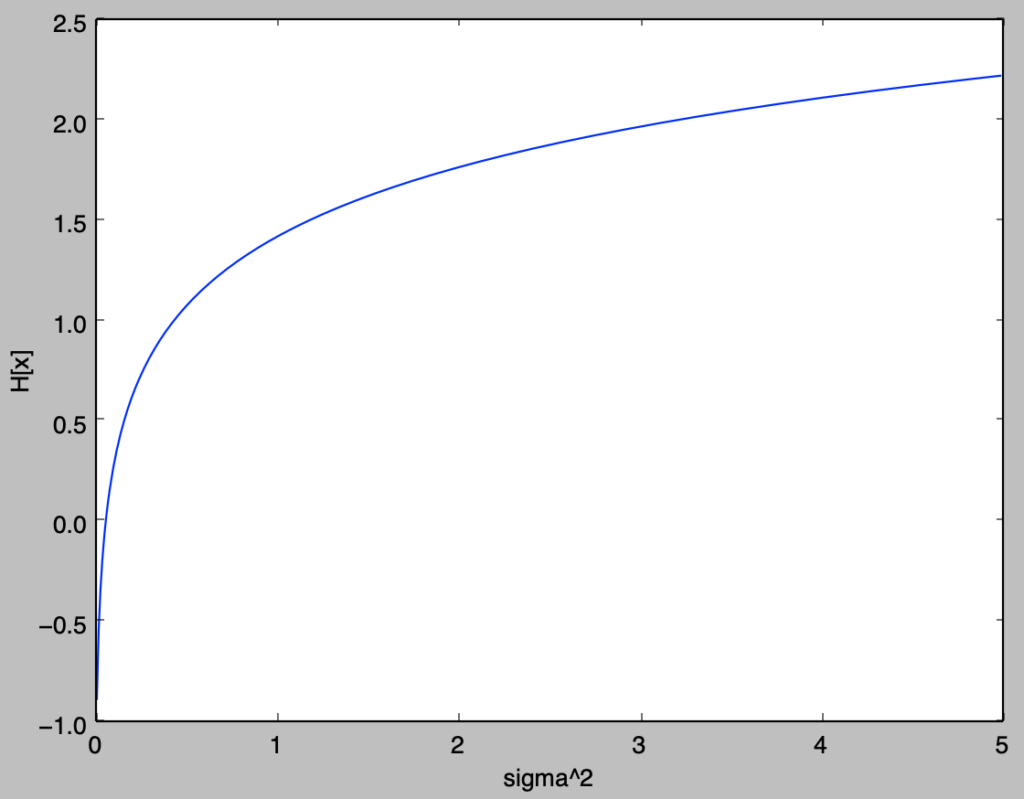
p(x|\sigma^2,q) = \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp \left( -\frac{|x|^{q}}{2 \sigma^2} \right) \quad (2.293)
\end{align}
$$
・$(2.293)$式が正規化されていることの確認
$(2.293)$式は$x=0$で線対称であるので、区間$0 \leq x \leq \infty$での積分を計算し$2$倍することで全区間での積分が得られる。$0 \leq x \leq \infty$の区間での$(2.293)$式の積分は下記のように表せる。
$$
\large
\begin{align}
\int_{0}^{\infty} p(x|\sigma^2,q) dx = \int_{0}^{\infty} \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp \left( -\frac{x^{q}}{2 \sigma^2} \right) dx \quad (1)
\end{align}
$$
上記に対して$\displaystyle u = \frac{x^{q}}{2 \sigma^2}$で変数変換を行うことを考える。このとき$\displaystyle x = (2 \sigma^2 u)^{\frac{1}{q}}$より$\displaystyle \frac{dx}{du}$は下記のように計算できる。
$$
\large
\begin{align}
\frac{dx}{du} &= \frac{d}{du} (2 \sigma^2 u)^{\frac{1}{q}} \\
&= \frac{1}{q} (2 \sigma^2)^{\frac{1}{q}} u^{\frac{1}{q}-1}
\end{align}
$$
また、$0 \leq x \leq \infty$に対応する$u$の区間は$0 \leq u \leq \infty$である。よって$(1)$式は下記のように変数を置換できる。
$$
\large
\begin{align}
\int_{0}^{\infty} p(x|\sigma^2,q) dx &= \int_{0}^{\infty} \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp \left( -\frac{x^{q}}{2 \sigma^2} \right) dx \quad (1) \\
&= \int_{0}^{\infty} \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp(-u) \times \frac{dx}{du} du \\
&= \int_{0}^{\infty} \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp(-u) \times \frac{1}{q} (2 \sigma^2)^{\frac{1}{q}} u^{\frac{1}{q}-1} du \\
&= \frac{1}{2 \Gamma(1/q)} \int_{0}^{\infty} u^{\frac{1}{q}-1} \exp(-u) du \\
&= \frac{\Gamma(1/q)}{2 \Gamma(1/q)} = \frac{1}{2}
\end{align}
$$
したがって下記が成立する。
$$
\large
\begin{align}
\int_{-\infty}^{\infty} p(x|\sigma^2,q) dx &= 2 \int_{0}^{\infty} p(x|\sigma^2,q) dx \\
&= 2 \times \frac{1}{2} = 1 \quad (2.294)
\end{align}
$$
・$(2.293)$式に$q=2$を代入すると正規分布が得られることの確認
$(2.293)$式に$q=2$を代入すると下記が得られる。
$$
\large
\begin{align}
p(x|\sigma^2,q) &= \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp \left( -\frac{|x|^{q}}{2 \sigma^2} \right) \quad (2.293) \\
&= \frac{2}{2 (2 \sigma^2)^{1/2} \Gamma(1/2)} \exp \left( -\frac{|x|^{2}}{2 \sigma^2} \right) \\
&= \frac{1}{(2 \pi \sigma^2)^{1/2}} \exp \left( -\frac{x^{2}}{2 \sigma^2} \right) = \mathcal{N}(0,\sigma^2)
\end{align}
$$
上記の導出にあたって、$\Gamma(1/2)=\sqrt{\pi}$であることを用いた。
・対数尤度が$(2.295)$式で得られることの確認
$(2.293)$式に基づいて同時確率$p(\mathbf{t}|\mathbf{X},\mathbf{w},\sigma^2)$は下記のように得られる。
$$
\large
\begin{align}
p(\mathbf{t}|\mathbf{X},\mathbf{w},\sigma^2) &= \prod_{n=1}^{N} \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp \left( -\frac{|t_{n}-y(\mathbf{x}_{n},\mathbf{w})|^{q}}{2 \sigma^2} \right)
\end{align}
$$
尤度関数は上記を$\mathbf{w},\sigma^2$を変数と見なした関数であるので、上記は下記のように整理できる。
$$
\large
\begin{align}
p(\mathbf{t}|\mathbf{X},\mathbf{w},\sigma^2) &= \prod_{n=1}^{N} \frac{q}{2 (2 \sigma^2)^{1/q} \Gamma(1/q)} \exp \left( -\frac{|t_{n}-y(\mathbf{x}_{n},\mathbf{w})|^{q}}{2 \sigma^2} \right) \\
&= \prod_{n=1}^{N} \exp \left( -\frac{|t_{n}-y(\mathbf{x}_{n},\mathbf{w})|^{q}}{2 \sigma^2} – \frac{1}{q}\ln{(2 \sigma^2)} + \mathrm{Const.} \right) \\
&= \exp \left( – \sum_{n=1}^{N} \frac{|t_{n}-y(\mathbf{x}_{n},\mathbf{w})|^{q}}{2 \sigma^2} – \frac{N}{q}\ln{(2 \sigma^2)} + \mathrm{Const.}’ \right)
\end{align}
$$
対数尤度は上記の対数を取ることで得られる。
$$
\large
\begin{align}
\ln{p(\mathbf{t}|\mathbf{X},\mathbf{w},\sigma^2)} &= \ln{ \left[ \exp \left( – \sum_{n=1}^{N} \frac{|t_{n}-y(\mathbf{x}_{n},\mathbf{w})|^{q}}{2 \sigma^2} – \frac{N}{q}\ln{(2 \sigma^2)} + \mathrm{Const.}’ \right) \right] } \\
&= – \sum_{n=1}^{N} \frac{|t_{n}-y(\mathbf{x}_{n},\mathbf{w})|^{q}}{2 \sigma^2} – \frac{N}{q}\ln{(2 \sigma^2)} + \mathrm{Const.}’ \quad (2.295)
\end{align}
$$
よって$(2.295)$式が対数尤度に対応すると考えられる。
問題$2.44$
サンプル$\mathbf{X}$が観測された際の尤度を$p(\mathbf{X}|\mu,\lambda)$とおくと、$p(\mathbf{X}|\mu,\lambda)$に関して下記が成立する。
$$
\large
\begin{align}
p(\mathbf{X}|\mu,\lambda) & \propto \left[ \lambda^{1/2} \exp \left( -\frac{\lambda \mu^{2}}{2} \right) \right]^{N} \exp \left[ \lambda \mu \sum_{n=1}^{N} x_n – \frac{\lambda}{2} \sum_{n=1}^{N} x_{n}^{2} \right] \quad (2.152)
\end{align}
$$
このとき上記と同じような関数形の事前分布は下記のように考えることができる。
$$
\large
\begin{align}
p(\mu,\lambda) & \propto \left[ \lambda^{1/2} \exp \left( -\frac{\lambda \mu^{2}}{2} \right) \right]^{N} \exp \left[ c \lambda \mu – d \lambda \right] \\
&= \exp \left[ – \frac{\beta \lambda}{2} \left( \mu – \frac{c}{\beta} \right)^2 \right] \times \lambda^{\beta/2} \exp \left[ – \left( d – \frac{c^2}{2 \beta} \right) \lambda \right] \quad (2.153)
\end{align}
$$
上記のように表された$(2.153)$の正規化を行えば正規分布$\displaystyle \mathcal{N} \left( \frac{c}{\beta}, (\beta \lambda)^{-1} \right)$とガンマ分布$\displaystyle \mathrm{Gamma} \left( \frac{\beta}{2}+1,d – \frac{c^2}{2 \beta} \right)$の積に一致すると考えることができる。よって、$\displaystyle \mu_{0} \frac{c}{\beta}, a=\frac{\beta}{2}+1, b=d – \frac{c^2}{2 \beta}$のようにおくと$(2.154)$式の比例に一致する。
よって$(2.154)$式の正規-ガンマ分布を事前分布に定めると、事後分布も正規ガンマ分布となると考えられる。
$$
\large
\begin{align}
p(\mu,\lambda) = \mathcal{N}(\mu|\mu_{0},(\beta \lambda)^{-1}) \mathrm{Gam}(\lambda|a_{0},b_{0}) \quad (2.154)
\end{align}
$$
以下、事前分布$p(\mu,\lambda)$のパラメータを$\mu_{0}, a_{0}, b_{0}$、事後分布$p(\mu,\lambda|\mathbf{X})$のパラメータを$\mu_{N}, a_{N}, b_{N}$のようにおき、事後分布のパラメータの式の導出を行う。
$$
\large
\begin{align}
& p(\mu_{N},\lambda_{N}|\mathbf{X}) \propto p(\mathbf{X}|\mu,\lambda) p(\mu_{0},\lambda) \\
& \propto \left[ \lambda^{1/2} \exp \left( -\frac{\lambda \mu^{2}}{2} \right) \right]^{N} \exp \left[ \lambda \mu \sum_{n=1}^{N} x_n – \frac{\lambda}{2} \sum_{n=1}^{N} x_{n}^{2} \right] \times \mathcal{N}(\mu|\mu_{0},(\beta_{0} \lambda)^{-1}) \mathrm{Gam}(\lambda|a_{0},b_{0}) \\
& \propto \lambda^{N/2} \exp \left( -\frac{\lambda N \mu^{2}}{2} \right) \exp \left[ \lambda \mu \sum_{n=1}^{N} x_n – \frac{\lambda}{2} \sum_{n=1}^{N} x_{n}^{2} \right] \times \exp \left[ -\frac{\beta \lambda(\mu-\mu_{0})^2}{2} \right] \lambda^{a_{0}-1} \exp(-b_{0} \lambda) \\
&= \exp \left[ -\frac{\lambda}{2}\left( N + \beta \right) \mu^2 + \left( \sum_{n=1}^{N}x_n + \beta \mu_{0} \right) \mu \right] \lambda^{a_{0}+\frac{N}{2}-1} \exp \left[ -\left( b_{0} + \frac{\beta \mu_{0}^{2}}{2} \right) \lambda \right] \\
&= \exp \left[ -\frac{\lambda(N + \beta)}{2}\left( \mu – \frac{ \displaystyle \sum_{n=1}^{N}x_n + \beta \mu_{0}}{N + \beta} \right)^2 \right] \lambda^{a_{0}+\frac{N}{2}-1} \exp \left[ -\left( b_{0} + \frac{\beta \mu_{0}^{2}}{2} – \frac{ \displaystyle \left( \sum_{n=1}^{N}x_n + \beta \mu_{0} \right)^2}{2(N + \beta)} \right) \lambda \right]
\end{align}
$$
よって、$\mu_{N}, a_{N}, b_{N}$はそれぞれ下記のように得られる。
$$
\large
\begin{align}
\mu_{N} &= \frac{ \displaystyle \sum_{n=1}^{N}x_n + \beta \mu_{0}}{N + \beta} \\
a_{N} &= a_{0}+\frac{N}{2}-1 \\
b_{N} &= b_{0} + \frac{\beta \mu_{0}^{2}}{2} – \frac{ \displaystyle \left( \sum_{n=1}^{N}x_n + \beta \mu_{0} \right)^2}{2(N + \beta)}
\end{align}
$$
問題$2.45$
多次元正規分布の確率密度関数$\mathcal{N}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda}^{-1})$は下記のように表される。
$$
\large
\begin{align}
\mathcal{N}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda}^{-1}) = \frac{|\Lambda|^{1/2}}{(2 \pi)^{D/2}} \exp \left[ -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Lambda} (\mathbf{x}-\mathbf{\mu}) \right]
\end{align}
$$
このとき、$\mathbf{x}_{1},…,\mathbf{x}_{N}$に関する尤度を$L(\mathbf{\Lambda})$とおくと、$L(\mathbf{\Lambda})$は下記のように表せる。
$$
\large
\begin{align}
L(\mathbf{\Lambda}) &= \prod_{n=1}^{N} \mathcal{N}(\mathbf{x}_{n}|\mathbf{\mu},\mathbf{\Lambda}^{-1}) \\
&= \prod_{n=1}^{N} \frac{|\mathbf{\Lambda}|^{1/2}}{(2 \pi)^{D/2}} \exp \left[ -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Lambda} (\mathbf{x}-\mathbf{\mu}) \right] \\
&= \frac{|\mathbf{\Lambda}|^{N/2}}{(2 \pi)^{ND/2}} \exp \left[ -\frac{1}{2} \sum_{n=1}^{N} (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Lambda}(\mathbf{x}-\mathbf{\mu}) \right] \quad (1)
\end{align}
$$
上記の$(1)$式を$\Lambda$に関する式と見た際に$(2.155)$式と同様の関数形であることを以下に示す。
$$
\large
\begin{align}
L(\mathbf{\Lambda}) & \propto |\mathbf{\Lambda}|^{N/2} \exp \left[ -\frac{1}{2} \sum_{n=1}^{N} (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Lambda}(\mathbf{x}-\mathbf{\mu}) \right] \quad (1)’ \\
&= |\mathbf{\Lambda}|^{N/2} \exp \left[ -\frac{1}{2} \sum_{n=1}^{N} \mathrm{Tr}((\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Lambda}(\mathbf{x}-\mathbf{\mu})) \right] \\
&= |\mathbf{\Lambda}|^{N/2} \exp \left[ -\frac{1}{2} \sum_{n=1}^{N} \mathrm{Tr}((\mathbf{x}-\mathbf{\mu})(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Lambda}) \right] \\
&= |\mathbf{\Lambda}|^{N/2} \exp \left[ -\frac{1}{2} \mathrm{Tr} \left( \sum_{n=1}^{N} (\mathbf{x}-\mathbf{\mu})(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Lambda} \right) \right] \\
&= |\mathbf{\Lambda}|^{N/2} \exp \left[ -\frac{1}{2} \mathrm{Tr}(\mathbf{S}\mathbf{\Lambda}) \right] \quad (2) \\
\mathbf{S} &= \sum_{n=1}^{N} (\mathbf{x}-\mathbf{\mu})(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}
\end{align}
$$
$(2.155)$式は$\Lambda$に関して$(2)$式と同様な関数形であるので、共役事前分布であると考えることができる。
問題$2.46$
$$
\large
\begin{align}
p(x|\mu,a,b) = \int_{0}^{\infty} \mathcal{N}(x|\mu,\tau^{-1}) \mathrm{Gam}(\tau|a,b) \quad (2.158)
\end{align}
$$
上記で表した$(2.158)$式に対して下記のように変形を考えられる。
$$
\large
\begin{align}
p(x|\mu,a,b) &= \int_{0}^{\infty} \mathcal{N}(x|\mu,\tau^{-1}) \mathrm{Gam}(\tau|a,b) d \tau \quad (2.158) \\
&= \int_{0}^{\infty} \left( \frac{\tau}{2 \pi} \right)^{1/2} \exp \left( -\frac{\tau(x-\mu)^2}{2} \right) \times \frac{b^{a} \tau^{a-1} e^{-b \tau}}{\Gamma(a)} d \tau \\
&= \frac{b^{a}}{\Gamma(a) \sqrt{2 \pi}} \int_{0}^{\infty} \sqrt{\tau} \exp \left( -\frac{\tau(x-\mu)^2}{2} \right) \times \tau^{a-1} e^{-b \tau} d \tau \\
&= \frac{b^{a}}{\Gamma(a) \sqrt{2 \pi}} \int_{0}^{\infty} \tau^{a+\frac{1}{2}-1} \exp \left( -\tau \left[ b + \frac{(x-\mu)^2}{2} \right] \right) d \tau \\
&= \frac{b^{a}}{\Gamma(a) \sqrt{2 \pi}} \times \Gamma \left( a+\frac{1}{2} \right) \left[ b + \frac{(x-\mu)^2}{2} \right]^{-a-\frac{1}{2}} \quad (1)
\end{align}
$$
上記に対し、$\displaystyle \nu = 2a, \lambda=\frac{a}{b}$のように文字を置き換えることを考える。$a, b$に関して解くと$\displaystyle a = \frac{\nu}{2}, b = \frac{\nu}{2 \lambda}$なので、それぞれ$(1)$式に代入を行う。
$$
\large
\begin{align}
p(x|\mu,a,b) &= \frac{b^{a}}{\Gamma(a) \sqrt{2 \pi}} \times \Gamma \left( a+\frac{1}{2} \right) \left[ b + \frac{(x-\mu)^2}{2} \right]^{-a-\frac{1}{2}} \quad (1) \\
&= \frac{\displaystyle \left( \frac{\nu}{2 \lambda} \right)^{\frac{\nu}{2}}}{\displaystyle \Gamma \left( \frac{\nu}{2} \right) \sqrt{2 \pi}} \times \Gamma \left( \frac{\nu+1}{2} \right) \left[ \frac{\nu}{2 \lambda} + \frac{(x-\mu)^2}{2} \right]^{-\frac{\nu+1}{2}} \\
&= \frac{\displaystyle \Gamma \left( \frac{\nu+1}{2} \right)}{\displaystyle \Gamma \left( \frac{\nu}{2} \right) \sqrt{2 \pi}} \times \left( \frac{\nu}{2 \lambda} \right)^{-\frac{1}{2}} \left( \frac{\nu}{2 \lambda} \right)^{\frac{\nu+1}{2}} \times \left[ \frac{\nu}{2 \lambda} + \frac{(x-\mu)^2}{2} \right]^{-\frac{\nu+1}{2}} \\
&= \frac{\displaystyle \Gamma \left( \frac{\nu+1}{2} \right)}{\displaystyle \Gamma \left( \frac{\nu}{2} \right) \sqrt{2 \pi}} \times \sqrt{ \frac{2 \lambda}{\nu} } \times \left[ \frac{2 \lambda}{\nu} \left( \frac{\nu}{2 \lambda} + \frac{(x-\mu)^2}{2} \right) \right]^{-\frac{\nu+1}{2}} \\
&= \frac{\displaystyle \Gamma \left( \frac{\nu+1}{2} \right)}{\displaystyle \Gamma \left( \frac{\nu}{2} \right)} \sqrt{ \frac{\lambda}{\pi \nu} } \times \left[ 1 + \frac{\lambda(x-\mu)^2}{\nu} \right]^{-\frac{\nu+1}{2}} \\
&= \mathrm{St}(x|\mu,\lambda,\nu) \quad (2.159)
\end{align}
$$
上記のように考えることで$(2.158)$から$(2.159)$を示せる。
問題$2.47$
下記で詳しく取り扱った。
・現代数理統計学 演習$4.5$
問題$2.48$
$$
\large
\begin{align}
\mathrm{St}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda},\nu) = \int_{0}^{\infty} \mathcal{N}(\mathbf{x}|\mathbf{\mu},(\eta\mathbf{\Lambda})^{-1}) \mathrm{Gam} \left(\eta \Bigr| \frac{\nu}{2}, \frac{\nu}{2} \right) d \eta \quad (2.261)
\end{align}
$$
上記で表した$(2.261)$式に出てくる、$\mathcal{N}(\mathbf{x}|\mathbf{\mu},(\eta\mathbf{\Lambda})^{-1})$と$\displaystyle \mathrm{Gam} \left(\eta \Bigr| \frac{\nu}{2}, \frac{\nu}{2} \right)$はそれぞれ下記のように表せる。
・$\mathcal{N}(\mathbf{x}|\mathbf{\mu},(\eta\mathbf{\Lambda})^{-1})$
$$
\large
\begin{align}
\mathcal{N}(\mathbf{x}|\mathbf{\mu},(\eta\mathbf{\Lambda})^{-1}) &= \frac{|\eta \mathbf{\Lambda}|^{1/2}}{(2 \pi)^{D/2}} \exp \left[ – \frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}(\eta \mathbf{\Lambda})(\mathbf{x}-\mathbf{\mu}) \right] \\
&= \frac{\eta^{D/2}|\mathbf{\Lambda}|^{1/2}}{(2 \pi)^{D/2}} \exp \left[ – \frac{\eta}{2} \Delta^{2} \right] \quad (1) \\
\Delta^2 &= (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{\Lambda}(\mathbf{x}-\mathbf{\mu})
\end{align}
$$
・$\displaystyle \mathrm{Gam} \left(\eta \Bigr| \frac{\nu}{2}, \frac{\nu}{2} \right)$
$$
\large
\begin{align}
\mathrm{Gam} \left(\eta \Bigr| \frac{\nu}{2}, \frac{\nu}{2} \right) = \frac{\displaystyle \left( \frac{\nu}{2} \right)^{\nu/2}}{\displaystyle \Gamma \left( \frac{\nu}{2} \right)} \eta^{\frac{\nu}{2}-1} \exp \left( – \frac{\nu \eta}{2} \right) \quad (2)
\end{align}
$$
$(1)$式、$(2)$式より、$(2.261)$式は下記のように変形できる。
$$
\large
\begin{align}
& \mathrm{St}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda},\nu) = \int_{0}^{\infty} \mathcal{N}(\mathbf{x}|\mathbf{\mu},(\eta\mathbf{\Lambda})^{-1}) \mathrm{Gam} \left(\eta \Bigr| \frac{\nu}{2}, \frac{\nu}{2} \right) d \eta \quad (2.261) \\
&= \int_{0}^{\infty} \frac{\eta^{D/2}|\mathbf{\Lambda}|^{1/2}}{(2 \pi)^{D/2}} \exp \left[ – \frac{\eta}{2} \Delta^{2} \right] \times \frac{\displaystyle \left( \frac{\nu}{2} \right)^{\nu/2}}{\displaystyle \Gamma \left( \frac{\nu}{2} \right)} \eta^{\frac{\nu}{2}-1} \exp \left( – \frac{\nu \eta}{2} \right) d \eta \\
&= \frac{|\mathbf{\Lambda}|^{1/2}}{(2 \pi)^{D/2}} \frac{\displaystyle \left( \frac{\nu}{2} \right)^{\nu/2}}{\displaystyle \Gamma \left( \frac{\nu}{2} \right)} \int_{0}^{\infty} \eta^{\frac{D+\nu}{2}-1} \exp \left[ – \eta \left( \frac{\nu+\Delta^2}{2} \right) \right] d \eta \\
&= \frac{|\mathbf{\Lambda}|^{1/2}}{(2 \pi)^{D/2}} \frac{\displaystyle \left( \frac{\nu}{2} \right)^{\nu/2}}{\displaystyle \Gamma \left( \frac{\nu}{2} \right)} \frac{\displaystyle \Gamma \left( \frac{D+\nu}{2} \right)}{\displaystyle \left( \frac{\nu+\Delta^2}{2} \right)^{\frac{D+\nu}{2}}} \\
&= \frac{\displaystyle \Gamma \left( \frac{\nu}{2} \right)}{\displaystyle \Gamma \left( \frac{D+\nu}{2} \right)} \frac{|\mathbf{\Lambda}|^{1/2} \nu^{\nu/2}}{\displaystyle \pi^{D/2} 2^{(D+\nu)/2} \nu^{(D+\nu)/2} \left( \frac{1+\Delta^2/\nu}{2} \right)^{\frac{D+\nu}{2}}} \\
&= \frac{\displaystyle \Gamma \left( \frac{\nu}{2} \right)}{\displaystyle \Gamma \left( \frac{D+\nu}{2} \right)} \frac{|\mathbf{\Lambda}|^{1/2}}{\displaystyle (\pi \nu)^{D/2} \left( 1+\frac{\Delta^2}{\nu} \right)^{\frac{D+\nu}{2}}} \\
&= \frac{\displaystyle \Gamma \left( \frac{\nu}{2} \right)}{\displaystyle \Gamma \left( \frac{D+\nu}{2} \right)} \frac{|\mathbf{\Lambda}|^{1/2}}{\displaystyle (\pi \nu)^{D/2}} \left( 1+\frac{\Delta^2}{\nu} \right)^{-\frac{D+\nu}{2}} \quad (2.162)
\end{align}
$$
ここまでの導出により、$(2.162)$式が成立することを示せた。
問題$2.50$
$$
\large
\begin{align}
\mathrm{St}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda},\nu) &= \frac{\displaystyle \Gamma \left( \frac{\nu}{2} \right)}{\displaystyle \Gamma \left( \frac{D+\nu}{2} \right)} \frac{|\mathbf{\Lambda}|^{1/2}}{\displaystyle (\pi \nu)^{D/2}} \left( 1+\frac{\Delta^2}{\nu} \right)^{-\frac{D+\nu}{2}} \quad (2.162) \\
\Delta^2 &= (\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{\Lambda}(\mathbf{x}-\mathbf{\mu}) \quad (2.163)
\end{align}
$$
$(2.162)$式を$\mathbf{x}$の関数と見ると、下記のように考えることができる。
$$
\large
\begin{align}
\mathrm{St}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda},\nu) & \propto \left( 1+\frac{\Delta^2}{\nu} \right)^{-\frac{D+\nu}{2}} \\
&= \left( 1+\frac{\Delta^2}{\nu} \right)^{-\frac{D}{2}} \times \left( 1+\frac{\Delta^2}{\nu} \right)^{-\frac{\nu}{2}} \\
&= \left( 1+\frac{\Delta^2}{\nu} \right)^{-\frac{D}{2}} \times \left[ \left( 1+\frac{\Delta^2}{\nu} \right)^{\frac{\nu}{\Delta^2}} \right]^{-\frac{\Delta^2}{2}}
\end{align}
$$
上記に対して$\nu \to \infty$を考えると$\displaystyle \frac{\nu}{\Delta^2} \to \infty$より下記が成立する。
$$
\large
\begin{align}
\lim_{\nu \to \infty} \mathrm{St}(\mathbf{x}|\mathbf{\mu},\mathbf{\Lambda},\nu) & \propto \lim_{\frac{\nu}{\Delta^2} \to \infty} \left( 1+\frac{\Delta^2}{\nu} \right)^{-\frac{D}{2}} \times \left[ \left( 1+\frac{\Delta^2}{\nu} \right)^{\frac{\nu}{\Delta^2}} \right]^{-\frac{\Delta^2}{2}} \\
&= 1 \times \exp \left[ -\frac{\Delta^2}{2} \right] \\
&= \exp \left[ -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^{\mathrm{T}}\mathbf{\Lambda}(\mathbf{x}-\mathbf{\mu}) \right]
\end{align}
$$
よって$\nu \to \infty$のとき$(2.262)$式は多次元正規分布$\mathcal{N}(\mathbf{\mu},\mathbf{\Lambda}^{-1})$に収束する。
問題$2.51$
・$(2.177)$式$\cos^{2}{A} + \sin^{2}{A} = 1$の導出
$\exp(iA)\exp(-iA) = 1$に$(2.296)$式を代入すると下記のように変形を行える。
$$
\large
\begin{align}
\exp(iA)\exp(-iA) &= 1 \\
(\cos{A} + i\sin{A})(\cos{A} – i\sin{A}) &= 1 \\
\cos^2{A} – i^2\sin^2{A} &= 1 \\
\cos^2{A} + \sin^2{A} &= 1
\end{align}
$$
・$(2.178)$式$\cos{A}\cos{B}+\sin{A}\sin{B}=\cos{(A-B)}$の導出
$(2.298)$式$\cos(A-B) = \mathrm{Re}[\exp{(i(A-B))}]$の右辺は下記のように変形を行える。
$$
\large
\begin{align}
\mathrm{Re}[\exp{(i(A-B))}] &= \mathrm{Re}[\exp{iA)}\exp{(-iB)}] \\
&= \mathrm{Re}[(\cos{A} + i\sin{A})(\cos{B} – i\sin{B})] \\
&= \mathrm{Re}[\cos{A}\cos{B} – i\cos{A}\sin{B} + i\sin{A}\cos{B} – i^2\sin{A}\sin{B}] \\
&= \mathrm{Re}[\cos{A}\cos{B} + \sin{A}\sin{B} + i(-\cos{A}\sin{B} + \sin{A}\cos{B})] \\
&= \cos{A}\cos{B} + \sin{A}\sin{B}
\end{align}
$$
上記と$(2.298)$式より$\cos{A}\cos{B}+\sin{A}\sin{B}=\cos{(A-B)}$が成立する。
・$(2.183)$式$\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}$の導出
$$
\large
\begin{align}
\sin(A-B) = \mathrm{Im}[\exp{(i(A-B))}] \quad (1)
\end{align}
$$
上記の$(1)$の右辺は下記のように変形を行える。
$$
\large
\begin{align}
\mathrm{Im}[\exp{(i(A-B))}] &= \mathrm{Im}[\exp{iA)}\exp{(-iB)}] \\
&= \mathrm{Im}[(\cos{A} + i\sin{A})(\cos{B} – i\sin{B})] \\
&= \mathrm{Im}[\cos{A}\cos{B} – i\cos{A}\sin{B} + i\sin{A}\cos{B} – i^2\sin{A}\sin{B}] \\
&= \mathrm{Im}[\cos{A}\cos{B} + \sin{A}\sin{B} + i(-\cos{A}\sin{B} + \sin{A}\cos{B})] \\
&= \sin{A}\cos{B} – \cos{A}\sin{B}
\end{align}
$$
上記と$(1)$式より$\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}$が成立する。
・参考
三角関数の加法定理・倍角の公式 etc.
問題$2.53$
$$
\large
\begin{align}
\sum_{n=1}^{N} \sin(\theta_n-\theta_0) = 0 \quad (2.182)
\end{align}
$$
上記の$(2.182)$式を$\theta_{0}$に関して解けばよい。
$$
\large
\begin{align}
\sum_{n=1}^{N} \sin(\theta_n-\theta_0) &= 0 \quad (2.182) \\
\sum_{n=1}^{N} (\sin{\theta_n}\cos{\theta_0} – \cos{\theta_n}\sin{\theta_0}) &= 0 \\
\cos{\theta_0} \sum_{n=1}^{N} \sin{\theta_n} &= \sin{\theta_0} \sum_{n=1}^{N} \cos{\theta_n} \\
\sum_{n=1}^{N} \sin{\theta_n} &= \tan{\theta_0} \sum_{n=1}^{N} \cos{\theta_n} \\
\tan{\theta_0} &= \frac{\displaystyle \sum_{n=1}^{N} \sin{\theta_n}}{\displaystyle \sum_{n=1}^{N} \cos{\theta_n}} \\
\theta_0 &= \tan^{-1}{ \left[ \frac{\displaystyle \sum_{n=1}^{N} \sin{\theta_n}}{\displaystyle \sum_{n=1}^{N} \cos{\theta_n}} \right] }
\end{align}
$$
上記より$(2.184)$式の$\theta_{0}^{ML} = \tan^{-1}{ \left[ \frac{\displaystyle \sum_{n=1}^{N} \sin{\theta_n}}{\displaystyle \sum_{n=1}^{N} \cos{\theta_n}} \right] }$が成立する。
問題$2.54$
$$
\large
\begin{align}
p(\theta|\theta_{0},m) &= \frac{1}{2 \pi \mathit{I}_{0}(m)} \exp(m \cos(\theta-\theta_0)) \\
& \propto \exp(m \cos(\theta-\theta_0))
\end{align}
$$
$(2.179)$式は$\theta$を変数と見る場合上記のように考えることができる。このとき$f(\theta) = \exp(m \cos(\theta-\theta_0))$のようにおくと、$\theta = \theta_{0}, (\mod 2 \pi)$のときに$f(\theta)$が最大となり、$\theta = \theta_{0} + \pi, (\mod 2 \pi)$が示せれば$(2.179)$式に関しても同時に成立すると考えられる。よって、以下$f(\theta)$の$1$階微分$f'(\theta)$、$2$階微分$f^{”}(\theta)$を計算し、$f(\theta)$が最大・最小となる$\theta$の条件を導出する。
・$1$階微分$f'(\theta)$の計算
$$
\large
\begin{align}
f'(\theta) &= (\exp(m \cos(\theta-\theta_0)))’ \\
&= \exp(m \cos(\theta-\theta_0)) \times (-m) \sin(\theta-\theta_0) \\
&= -m \sin(\theta-\theta_0) \exp(m \cos(\theta-\theta_0))
\end{align}
$$
・$2$階微分$f^{”}(\theta)$の計算
$$
\large
\begin{align}
f^{”}(\theta) &= -m \cos(\theta-\theta_0) \exp(m \cos(\theta-\theta_0)) + m^2 \sin^{2}(\theta-\theta_0) \exp(m \cos(\theta-\theta_0)) \\
&= \left[ m^2 \sin^{2}(\theta-\theta_0) – m \cos(\theta-\theta_0) \right] \exp(m \cos(\theta-\theta_0))
\end{align}
$$
ここで$1$階微分$f'(\theta)$に関し、$f'(\theta)=0$となる$\theta$を導出することを考える。
$$
\large
\begin{align}
f'(\theta) &= 0 \\
m \sin(\theta-\theta_0) \exp(m \cos(\theta-\theta_0)) &= 0 \\
\sin(\theta-\theta_0) &= 0
\end{align}
$$
上記より$\theta = \theta_{0}, \theta_{0} + \pi, \mod 2 \pi$がここでの解であると考えられる。$f'(\theta)=0$は極値の必要条件であるので、それぞれの解に関して$f^{”}(\theta)$の符号を確認する。
・$f^{”}(\theta_{0})$の符号
$$
\large
\begin{align}
f^{”}(\theta_{0}) &= \left[ m^2 \sin^{2}(\theta_{0}-\theta_0) – m \cos(\theta_{0}-\theta_0) \right] \exp(m \cos(\theta_{0}-\theta_0)) \\
&= -m \exp(m) < 0
\end{align}
$$
・$f^{”}(\theta_{0} + \pi)$の符号
$$
\large
\begin{align}
f^{”}(\theta_{0} + \pi) &= \left[ m^2 \sin^{2}(\theta_{0}+\pi-\theta_0) – m \cos(\theta_{0}+\pi-\theta_0) \right] \exp(m \cos(\theta_{0}+\pi-\theta_0)) \\
&= m \exp(-m) > 0
\end{align}
$$
よって$\theta = \theta_{0}, \mod 2 \pi$のときに$(2.179)$式が最大となり、$\theta = \theta_{0} + \pi, \mod 2 \pi$のときに$(2.179)$式が最小となると考えることができる。
問題$2.56$
$x = \exp[\ln{x}]$が成立することを元に全ての項を指数関数の中に入れた後に変形を考えるとわかりやすいので、以下この方針に基づいて変形を行う。
・ベータ分布
$$
\large
\begin{align}
Beta(x|a,b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} x^{a-1} (1-x)^{b-1} \quad (2.13)
\end{align}
$$
ベータ分布の$(2.13)$式は上記のように表されるが、この式は下記のように変形することができる。
$$
\large
\begin{align}
Beta(x|a,b) &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} x^{a-1} (1-x)^{b-1} \quad (2.13) \\
&= \exp \left[ \ln{ \left( \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} x^{a-1} (1-x)^{b-1} \right) } \right] \\
&= \exp \left[ \ln{ \left( \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \right) + (a-1) \ln{x} + (b-1)\ln{(1-x)} } \right] \\
&= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \exp \left[ (a-1) \ln{x} + (b-1)\ln{(1-x)} \right] \\
&= h(\mathbf{x})g(a,b) \exp \left[ \eta^{\mathrm{T}} \mathbf{u}(\mathbf{x}) \right]
\end{align}
$$
上記の一番下の式では下記のように文字を置いた。
$$
\large
\begin{align}
h(\mathbf{x}) &= 1 \\
g(a,b) &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \\
\eta(a,b) &= \left(\begin{array}{c} a-1 \\ b-1 \end{array} \right) \\
\mathbf{u}(\mathbf{x}) &= \left(\begin{array}{c} \ln{x} \\ \ln{(1-x)} \end{array} \right)
\end{align}
$$
・ガンマ分布
$$
\large
\begin{align}
\mathrm{Gamma}(x|a,b) = \frac{b^{a}}{\Gamma(a)} \lambda^{a-1} \exp{(-b \lambda)} \quad (2.146)
\end{align}
$$
ベータ分布の$(2.146)$式は上記のように表されるが、この式は下記のように変形することができる。
$$
\large
\begin{align}
\mathrm{Gamma}(x|a,b) &= \frac{b^{a}}{\Gamma(a)} x^{a-1} \exp{(-b x)} \quad (2.146) \\
&= \frac{b^{a}}{\Gamma(a)} \exp[\ln{(x^{a-1})}] \exp{(-b x)} \\
&= \frac{b^{a}}{\Gamma(a)} \exp[(a-1)\ln{x} – bx] = h(\mathbf{x})g(a,b) \exp \left[ \eta^{\mathrm{T}} \mathbf{u}(\mathbf{x}) \right]
\end{align}
$$
上記の一番下の式では下記のように文字を置いた。
$$
\large
\begin{align}
h(\mathbf{x}) &= 1 \\
g(a,b) &= \frac{b^{a}}{\Gamma(a)} \\
\eta(a,b) &= \left(\begin{array}{c} a-1 \\ -b \end{array} \right) \\
\mathbf{u}(\mathbf{x}) &= \left(\begin{array}{c} \ln{x} \\ x \end{array} \right)
\end{align}
$$
・von Mises分布
$$
\large
\begin{align}
p(x|\theta_0,m) = \frac{1}{2 \pi \mathit{I}_{0}(m)} \exp \left[ m \cos(x-\theta_{0}) \right] \quad (2.179)
\end{align}
$$
von Mises分布の$(2.179)$式は上記のように表されるが、この式は下記のように変形することができる。
$$
\large
\begin{align}
p(x|\theta_0,m) &= \frac{1}{2 \pi \mathit{I}_{0}(m)} \exp \left[ m \cos(x-\theta_{0}) \right] \quad (2.179) \\
&= \frac{1}{2 \pi \mathit{I}_{0}(m)} \exp \left[ m ( \cos{x}\cos{\theta_{0}} + \sin{x}\sin{\theta_{0}} ) \right] \\
&= \frac{1}{2 \pi \mathit{I}_{0}(m)} \exp \left[ m \cos{x}\cos{\theta_{0}} + m \sin{x}\sin{\theta_{0}} \right] = h(\mathbf{x})g(\theta_0,m) \exp \left[ \eta^{\mathrm{T}} \mathbf{u}(\mathbf{x}) \right]
\end{align}
$$
上記の一番下の式では下記のように文字を置いた。
$$
\large
\begin{align}
h(\mathbf{x}) &= 1 \\
g(a,b) &= \frac{1}{2 \pi \mathit{I}_{0}(m)} \\
\eta(\theta_0,m) &= \left(\begin{array}{c} m \cos{\theta_{0}} \\ m \sin{\theta_{0}} \end{array} \right) \\
\mathbf{u}(\mathbf{x}) &= \left(\begin{array}{c} \cos{x} \\ \sin{x} \end{array} \right)
\end{align}
$$
問題$2.58$
$$
\large
\begin{align}
g(\eta) \int h(x) \exp \left[ \eta^{\mathrm{T}} u(x) \right] dx = 1 \quad (2.195)
\end{align}
$$
上記で表した$(2.195)$式を$2$階微分することを考える。
$$
\large
\begin{align}
& \nabla \nabla g(\eta) \int h(x) \exp \left[ \eta^{\mathrm{T}} u(x) \right] dx = 0 \\
& – \nabla \nabla g(\eta) \int h(x) \exp \left[ \eta^{\mathrm{T}} u(x) \right] dx = \nabla g(\eta) \int h(x) \exp \left[ \eta^{\mathrm{T}} u(x) \right] u(x) dx \\
& – \frac{1}{g(\eta)} \nabla \nabla g(\eta) = \int h(x) \exp \left[ \eta^{\mathrm{T}} u(x) \right] u(x) dx \nabla g(\eta)^{\mathrm{T}} + g(\eta) \int h(x) \exp \left[ \eta^{\mathrm{T}} u(x) \right] u(x) u(x)^{\mathrm{T}} dx \\
& – \nabla \nabla \ln{g(\eta)} = \mathbb{E}[u(x)] \times \frac{1}{g(\eta)} \nabla g(\eta)^{\mathrm{T}} + \mathbb{E}[u(x)u(x)^{\mathrm{T}}] \\
& – \nabla \nabla \ln{g(\eta)} = – \mathbb{E}[u(x)] \mathbb{E}[u(x)^{\mathrm{T}}] + \mathbb{E}[u(x)u(x)^{\mathrm{T}}] \\
& – \nabla \nabla \ln{g(\eta)} = – \mathrm{cov}[u(x)] \quad (2.300)
\end{align}
$$
上記より$(2.300)$式が成立することが確かめられる。
・参考
ヘッセ行列(Hessian matrix)
問題$2.59$
確率密度関数$f(x)$が正規化されている際に確率密度関数$\displaystyle \frac{1}{\sigma} f \left( \frac{x}{\sigma} \right)$も正規化されていることを示す。導出にあたっては$f(y)$を$\displaystyle y = \frac{x}{\sigma}$で変数変換した際の確率密度関数$g(x)$を考えれば良い。
$$
\large
\begin{align}
\frac{dy}{dx} = \frac{1}{\sigma}
\end{align}
$$
上記より、$g(x)$は下記のように表せる。
$$
\large
\begin{align}
g(x) &= f(y) \frac{dy}{dx} = f \left( \frac{x}{\sigma} \right) \frac{dy}{dx} \\
&= \frac{1}{\sigma} f \left( \frac{x}{\sigma} \right)
\end{align}
$$
ここで$g(x)$は正規化された確率密度関数であることより、$\displaystyle \frac{1}{\sigma} f \left( \frac{x}{\sigma} \right)$も正規化されていると考えられる。
・考察
変数変換を用いる際は変数変換後の確率密度関数$g(x)$を定義することで変数変換の公式をそのままあてはめることができ、考えやすいと思われる。