統計学を取り扱う上で凸関数(convex function)や凸集合(convex set)は様々な状況で用いられます。凸関数に関してはイェンセンの不等式(Jensen’s inequality)が成立し、統計学では期待値を用いて表されることも多いです。
当記事では統計学に関連して用いられる凸関数、イェンセンの不等式、凸集合などについて取りまとめを行いました。
Contents
凸関数
凸関数の定義
凸関数は関数$f(x)$上の$2$点$(a,f(a))$と$(b,f(b))$を元に定義される。$0 \leq t \leq 1$となる任意の$t$に対し下記が成立すれば、「関数$f(x)$が上に凸である」という。
$$
\large
\begin{align}
f(ta + (1-t)b) \geq tf(a) + (1-t)f(b) \quad (1)
\end{align}
$$
ここで$x=ta + (1-t)b$は$x=a$と$x=b$を$(1-t):t$に内分する点である。このことは下記の図を用いてベクトル計算を元に理解するとわかりやすい。
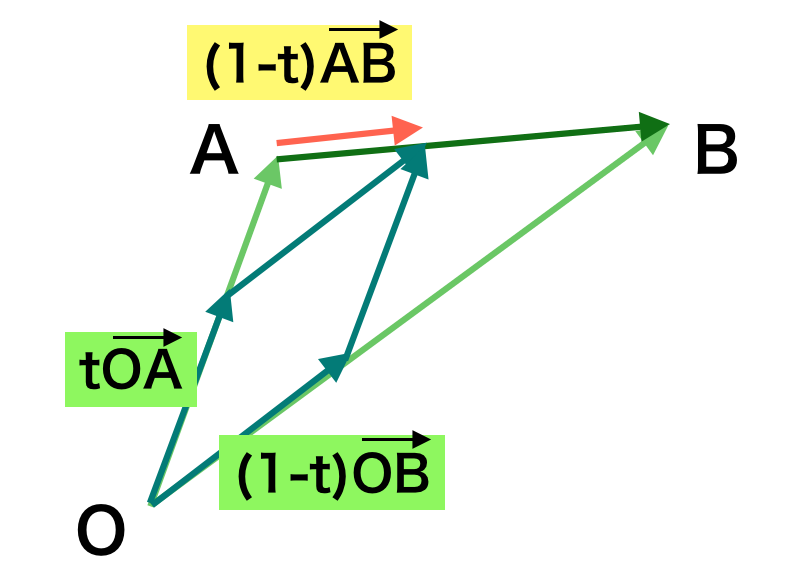
$$
\large
\begin{align}
t \overrightarrow{OA} + (1-t) \overrightarrow{OB} &= \overrightarrow{OA} \, – \, \overrightarrow{OA} + t \overrightarrow{OA} + (1-t) \overrightarrow{OB} \\
&= \overrightarrow{OA} + (t-1) \overrightarrow{OA} + (1-t) \overrightarrow{OB} \\
&= \overrightarrow{OA} \, – \, (1-t) \overrightarrow{OA} + (1-t) \overrightarrow{OB} \\
&= \overrightarrow{OA} + (1-t) \left( \overrightarrow{OB} \, – \, \overrightarrow{OA} \right) \\
&= \overrightarrow{OA} + (1-t) \overrightarrow{AB}
\end{align}
$$
また、「下に凸 $\iff$ $f^{”}(x) \geq 0$」、「上に凸 $\iff$ $f^{”}(x) \leq 0$」が成立する。よって凸関数であるかを調べる際には$2$階微分を計算することが多い。
$f(x)=x^2$の凸性
$f(x)=x^2$が下に凸であることを$f(ta + (1-t)b) \leq tf(a) + (1-t)f(b)$が成立することを元に示す。
$f(ta + (1-t)b) \leq tf(a) + (1-t)f(b) \iff tf(a) + (1-t)f(b)-f(ta + (1-t)b) \geq 0$のように考えられるので、以下、$tf(a) + (1-t)f(b)-f(ta + (1-t)b) \geq 0$を示す。
$$
\large
\begin{align}
tf(a) & + (1-t)f(b)-f(ta + (1-t)b) = t a^2 (1-t) b^2 – (ta + (1-t)b)^2 \\
&= t a^2 + (1-t) b^2 – (t^2a^2 + (1-t)^2b^2 + 2t(1-t)ab) \\
&= t(1-t) a^2 (1-t)(1-(1-t)) b^2 – 2t(1-t)ab \\
&= t(1-t) a^2 t(1-t) b^2 -2t(1-t)ab \\
&= t(1-t)(a^2+b^2-2ab) \\
&= t(1-t)(a-b)^2 \geq 0
\end{align}
$$
上記より$f(ta + (1-t)b) \leq tf(a) + (1-t)f(b)$が成立するので$f(x)=x^2$は下に凸の関数であることがわかる。
$f(x)=\log{x}$の凸性
$2$階微分の$f^{”}(x)$が$f^{”}(x) < 0$であることを用いて定義域$x>0$の$f(x)=\log{x}$が上に凸であることを示す。対数関数や分数関数の微分の公式より、$f'(x), f^{”}(x)$は下記のように計算できる。
$$
\large
\begin{align}
f'(x) &= (\log{x})’ \\
&= \frac{1}{x} \\
f^{”}(x) &= (f'(x))’ \\
&= \left( f'(x) \right)’ \\
&= – \frac{1}{x^2} < 0
\end{align}
$$
上記より$f^{”}(x) < 0$であるので、$f(x)=\log{x}$は上に凸の関数であることがわかる。
イェンセンの不等式
イェンセンの不等式の定義
$$
\large
\begin{align}
\lambda_i & \geq 0 \\
\sum_{i=1}^{M} \lambda_{i} &= 1
\end{align}
$$
上記のように$\lambda_1, \cdots , \lambda_M$を定義する。このとき上に凸の関数$f(x)$の任意の点$(x_i, f(x_i))$について下記の不等式が成立する。
$$
\large
\begin{align}
f \left( \sum_{i=1}^{M} \lambda_{i} x_{i} \right) \geq \sum_{i=1}^{M} \lambda_{i} f \left( x_{i} \right) \quad (2)
\end{align}
$$
上記の不等式をイェンセンの不等式という。イェンセンの不等式(Jensen’s inequality)は$(1)$式の凸関数の定義式と同様な式であり、厳密な導出は数学的帰納法を用いるなどによって示すことができる。数学的帰納法を用いた導出は下記で詳しく取り扱ったので当記事では省略する。
期待値とイェンセンの不等式
前項$(2)$式の$\lambda_{i}$について$\displaystyle \lambda_i \geq 0, \, \sum_{i=1}^{M} \lambda_i = 1$が成立することから、$\lambda_{i}$に確率関数$p(x_i)$を対応させることができる。このとき下記のような式が導出できる。
$$
\large
\begin{align}
f \left( \sum_{i=1}^{M} p(x_i) x_{i} \right) & \geq \sum_{i=1}^{M} p(x_i) f \left( x_{i} \right) \quad (2) \\
f \left( \mathbb{E} \left[ x_{i} \right] \right) & \geq \mathbb{E} \left[ f \left( x_{i} \right) \right] \quad (3)
\end{align}
$$
上記は、「上に凸の関数では点$(x_i, f(x_i))$の重心よりも重心における関数$f$の値が上にくる」と大まかに解釈すると良い。$(3)$式は離散型確率分布の式から導出したが、連続変数についても同様に下記が成立する。
$$
\large
\begin{align}
f \left( \mathbb{E} \left[ x_{i} \right] \right) & \geq \mathbb{E} \left[ f \left( x_{i} \right) \right] \quad (3) \\
f \left( \int x p(x) dx \right) & \geq \int f(x) p(x) dx
\end{align}
$$
凸集合
凸集合の定義
統計学での活用例
一様最強力不偏検定
リスクセット
下記の問題で取り扱ったように、統計的決定理論におけるリスク点の集合のリスクセットを考える際に確率化決定方式(randomized decision procedure)を含めるとリスクセットは凸集合となる。
https://www.hello-statisticians.com/explain-books-cat/math_stat_practice_ch5.html#55
