当記事では「統計学を学ぶにあたって必ず抑えておくべき微積分の定義・公式・基本事項」に関して取り扱います。特に微分の定義、$x^{n}$の微分の公式、微積分を用いた関数の最大・最小問題はあらゆるトピックで出てくるので、何度も繰り返して身につけておくと良いです。
取りまとめにあたっては数学の解説に関してはなるべくシンプルに取り扱いますが、統計学への応用に関連した複雑な内容に関しては目次に「*」をつけました。「*」がついているものはやや難しいので、読み飛ばしても問題ありません。
・基本数学まとめ
https://www.hello-statisticians.com/math_basic
Contents
微分
極限の概要
極限の定義を厳密に行うと抽象的であるので、当項では数$3$レベルの直感的な理解にとどめて以下、極限を取り扱う。
「極限」は「限りなく〇〇に近い数」と直感的には考えれば良い。たとえば限りなく$0$に近い数は$0.0001$、限りなく$2$に近い数は$1.99998$のように大まかに考えれば十分である。このように限りなく〇〇に近い数を下記のように定める。
$$
\large
\begin{align}
\lim_{x \to 1} x, \lim_{x \to \infty} x, \lim_{h \to 0} h
\end{align}
$$
上記では$\displaystyle \lim_{x \to 1} x$のように表したが、$\displaystyle \lim_{x \to 1} (x^2+x)$のように$x \to 1$のときの$x^2+x$の値を表すこともできる。
極限は基本的には$x \to 1$の際は$x=1$を代入することで考えることができる。たとえば下記が成立する。
$$
\large
\begin{align}
\lim_{x \to 1} x &= 1 \\
\lim_{x \to \infty} x &= \infty \\
\lim_{h \to 0} h &= 0 \\
\lim_{x \to 1} (x^2+x) &= (1^2+1) = 2 \\
\lim_{h \to 0} (h+1) &= (0+1) = 1
\end{align}
$$
上記のように極限は概ね代入を行うことで値の計算を行えるが、下記のような場合具体的な値を計算する際に注意が必要である。
$$
\large
\begin{align}
\lim_{x \to \infty} (2x-x), \lim_{h \to 0} \frac{h^2+h}{h}
\end{align}
$$
上記を単に代入することで計算を行おうとすると、下記のように表される。
$$
\large
\begin{align}
\lim_{x \to \infty} (2x-x) &= 2 \infty – \infty \quad (1) \\
\lim_{h \to 0} \frac{h^2+h}{h} &= \frac{0^2+0}{0} \quad (2)
\end{align}
$$
上記は「具体的に値が定まらない」ので不定形といわれる。「具体的に値が定まらない」というのはたとえば限りなく$0$に小さい数を表すにあたって$10^{-3}$を用いるときもあれば$10^{-10}$を用いるときもあると考えると理解しやすい。このように不定形では様々な値を持つことがあり得る。
よって、文字に関して約分などを行うことによって、予め不定形を解除する必要がある。$(1)$式$(2)$式の不定形はそれぞれ下記のように解消できる。
$$
\large
\begin{align}
\lim_{x \to \infty} (2x-x) &= \lim_{x \to \infty} x = \infty \quad (1)’ \\
\lim_{h \to 0} \frac{h^2+h}{h} &= \lim_{h \to 0} (h+1) \\
&= 1+0 = 1 \quad (2)’
\end{align}
$$
不定形の解消にあたっては上記のように約分で解消する場合が多い。また、不定形は具体的には$\displaystyle \frac{\infty}{\infty}$、$\displaystyle \frac{0}{0}$、$1^{\infty}$の形式で出てくることが多い。
当記事で取り扱う「微分の定義」は$\displaystyle \frac{0}{0}$の形式の不定形であるし、「ネイビア数$e$の定義」は$1^{\infty}$の形式の不定形である。
微分の定義式とその理解
$$
\large
\begin{align}
f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \quad (3)
\end{align}
$$
上記のように定義される$f'(x)$を「導関数」と呼ぶ。また、関数$f(x)$から導関数$f'(x)$を計算することを「微分」と称する。
上記のように定義される$f'(x)$を「導関数」と呼ぶ。また、関数$f(x)$から導関数$f'(x)$を計算することを「微分」と称する。$(3)$式のような微分の定義式だけではわかりにくいので、以下関数$f(x)$を元に導関数$f'(x)$が点$x$における$f(x)$の傾きを表す関数であることの確認を行う。
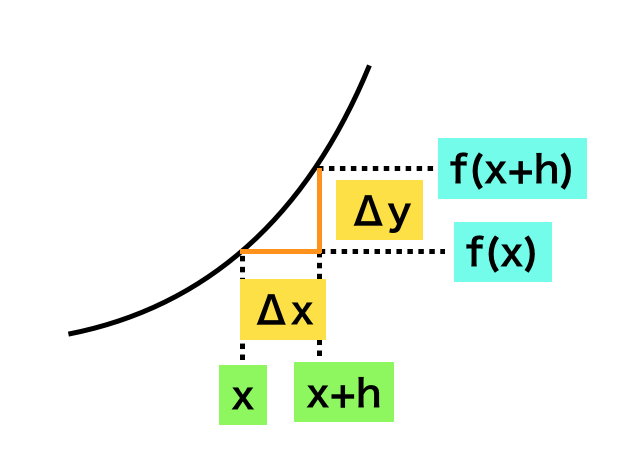
上図のように関数$y=f(x)$に対し、$x, x+h$における値$f(x), f(x+h)$を考えるとき、傾き$\displaystyle \frac{\Delta y}{\Delta x}$を下記のように考えられる。
$$
\large
\begin{align}
\frac{\Delta y}{\Delta x} &= \frac{f(x+h)-f(x)}{(x+h)-x} \\
&= \frac{f(x+h)-f(x)}{h}
\end{align}
$$
このとき、$h \to 0$を考えると$\displaystyle \frac{\Delta y}{\Delta x}$が$x$における$f(x)$の傾きに一致する。また、ここで$\displaystyle f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$であるので、導関数$f'(x)$は$f(x)$の$x$における傾きであると考えられる。
微分の定義に基づく$x^n$の微分
・$f(x) = x^2$
$$
\large
\begin{align}
f'(x) &= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\
&= \lim_{h \to 0} \frac{(x+h)^2-x^2}{h} \\
&= \lim_{h \to 0} \frac{(x^2+2xh+h^2)-x^2}{h} \\
&= \lim_{h \to 0} \frac{2xh+h^2}{h} \\
&= \lim_{h \to 0} \frac{\cancel{h}(2x+h)}{\cancel{h}} \\
&= \lim_{h \to 0} (2x+h) = 2x
\end{align}
$$
・$f(x) = x^3$
$$
\large
\begin{align}
f'(x) &= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\
&= \lim_{h \to 0} \frac{(x+h)^3-x^3}{h} \\
&= \lim_{h \to 0} \frac{(x^3+3x^2h+3xh^2+h^3)-x^3}{h} \\
&= \lim_{h \to 0} \frac{3x^2h+3xh^2+h^3}{h} \\
&= \lim_{h \to 0} \frac{\cancel{h}(3x^2+3xh+h^2)}{\cancel{h}} \\
&= \lim_{h \to 0} (3x^2+3xh+h^2) = 3x^2
\end{align}
$$
・$f(x) = x^n$
$$
\large
\begin{align}
f'(x) &= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\
&= \lim_{h \to 0} \frac{(x+h)^n-x^n}{h} \\
&= \lim_{h \to 0} \frac{(x^n + {}_n C_{1} x^{n-1}h + {}_n C_{2} x^{n-2}h^2 + \cdots + h^n) – x^n}{h} \\
&= \lim_{h \to 0} \frac{{}_n C_{1} x^{n-1}h + {}_n C_{2} x^{n-2}h^2 + \cdots + h^n}{h} \\
&= \lim_{h \to 0} \frac{\cancel{h}({}_n C_{1} x^{n-1} + {}_n C_{2} x^{n-2}h + \cdots + h^n)}{\cancel{h}} \\
&= \lim_{h \to 0} ({}_n C_{1} x^{n-1} + {}_n C_{2} x^{n-2}h + \cdots + h^n) \\
&= {}_n C_{1} x^{n-1} \\
&= n x^{n-1}
\end{align}
$$
積分
積分の定義・積分と微分の対応
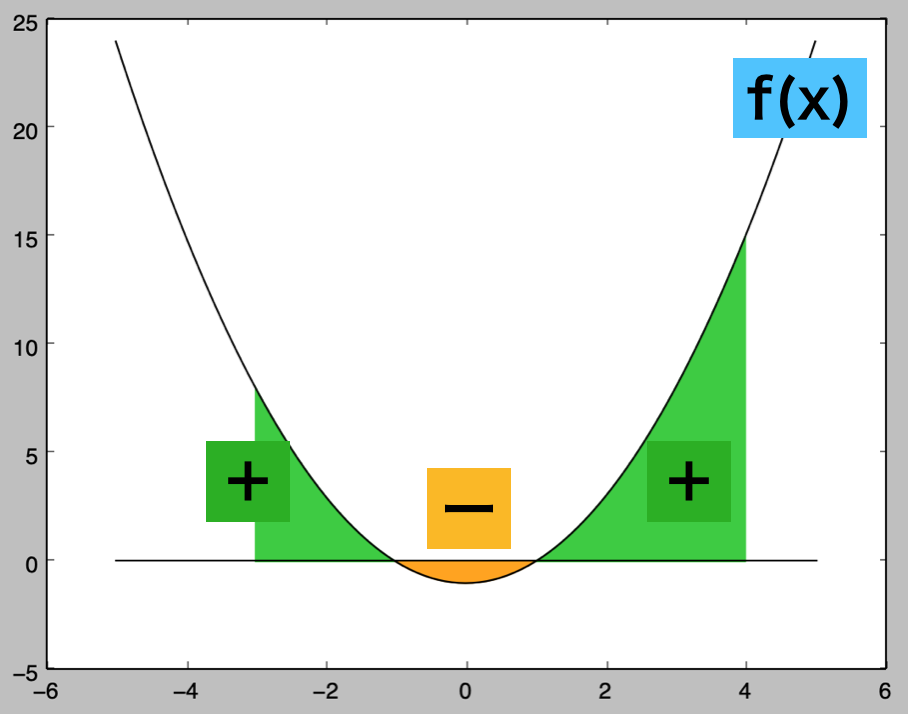
上図のように関数$f(x)=x^2-1$を考える際に、区間$[a,b]$における符号付き面積を下記のような数式で定める。
$$
\large
\begin{align}
\int_{a}^{b} f(x) dx
\end{align}
$$
上記の$\displaystyle \int$は$\displaystyle \sum$、$dx$は$\Delta x$に対応すると考えることで微小区間の和を取ることで符号付き面積を計算すると解釈できる。このとき下記が成立するように関数$F(x)$を定める。
$$
\large
\begin{align}
F(x) &= \int f(x) dx \\
\int_{a}^{b} f(x) dx &= F(b) – F(a)
\end{align}
$$
ここで上記に対し、$\displaystyle \frac{d}{dx} F(x)$を考えると下記が成立する。
$$
\large
\begin{align}
\frac{d}{dx} F(x) &= \lim_{\Delta x \to 0} \frac{1}{\Delta x}(F(x + \Delta x) – F(x)) \\
&= \lim_{\Delta x \to 0} \frac{1}{\Delta x} \left( \int_{a}^{x + \Delta x} f(t) dt – \int_{a}^{x} f(t) dt \right) \\
&= \lim_{\Delta x \to 0} \frac{1}{\Delta x} \int_{x}^{x + \Delta x} f(t) dt \\
&= \lim_{\Delta x \to 0} \frac{1}{\cancel{\Delta x}} f(x) \cancel{\Delta x} \\
&= f(x)
\end{align}
$$
よって関数$y=f(x)$と$y=0$によって構成される符号付き面積は微分の逆の計算を行うことによって導出できる。
多項式関数の定積分
前項で取り扱った内容より、$\displaystyle \frac{d}{dx} F(x) = \frac{d}{dx} \int f(x) dx = f(x)$が成立する。ここで$f(x)=x^n$のとき、$F(x)$は下記のように考えられる。
$$
\large
\begin{align}
\frac{d}{dx} F(x) &= f(x) = x^{n} \\
F(x) &= \int f(x) dx = \frac{1}{n+1} x^{n+1} + C
\end{align}
$$
ここで上記の$C$には任意の定数が対応し、この$C$は積分定数といわれることが多い。また、区間$[a,b]$での$y=x^n$と$y=0$に囲まれる符号付き面積は下記のように計算を行える。
$$
\large
\begin{align}
\int_{a}^{b} f(x) dx &= F(b)-F(a) \\
&= \left[ \frac{1}{n+1} x^{n+1} \right]_{a}^{b} \\
&= \frac{1}{n+1} (b^{n+1}-a^{n+1})
\end{align}
$$
上記の$\displaystyle \int_{a}^{b} f(x) dx$を関数$f(x)$の定積分という。ここでの手順に基づいて多項式関数の定積分を行うことができる。
積分と面積
前項で取り扱った内容より、積分を用いて多項式関数によって構成される面積の計算を行うことができる。前項では「符号付き面積」を計算したが、$y=0$の積分値が負で計算されるので、この部分の計算結果に$-$をかけることで補正を行う必要がある。
以下、$f(x)=x^2-1$の区間$[-2,3]$で$y=0$と$f(x)$がなす面積の計算を行う。$f(x)=x^2-1$は$x<-1,1<x$、$-1<x<1$で$f(x)<0$であることに基づいて面積$S$は下記のように計算できる。
$$
\large
\begin{align}
S &= \int_{-2}^{-1} f(x) dx – \int_{-1}^{1} f(x) dx + \int_{1}^{3} f(x) dx \\
&= \int_{-2}^{-1} (x^2-1) dx – \int_{-1}^{1} (x^2-1) dx + \int_{1}^{3} (x^2-1) dx \\
&= \left[ \frac{1}{3}x^3-x \right]_{-2}^{-1} – \left[ \frac{1}{3}x^3-x \right]_{-1}^{1} + \left[ \frac{1}{3}x^3-x \right]_{1}^{3} \\
&= \left[ \left( \frac{1}{3}(-1)^3-(-1) \right) – \left( \frac{1}{3}(-2)^3-(-2) \right) \right] – \left[ \left( \frac{1}{3} \cdot 1^3-1 \right) – \left( \frac{1}{3}(-1)^3-(-1) \right) \right] \\
& \qquad + \left[ \left( \frac{1}{3} \cdot 3^3-3 \right) – \left( \frac{1}{3} \cdot 1^3-1 \right) \right] \\
&= \left( \frac{2}{3} + \frac{2}{3} \right) – \left( – \frac{2}{3} – \frac{2}{3} \right) + \left( 6 + \frac{2}{3} \right) \\
&= \frac{28}{3}
\end{align}
$$
微積分の応用
最小値・最大値問題と微分
微分の応用でよく出てくるのが「最小値・最大値問題」である。統計学や機械学習の分野でよく用いられる「数理最適化」に関するトピックの多くが「最小値・最大値問題」に関連していることから、「最適化」の理解にあたっては微分の理解が必須となる。
以下$f(x)=-x^2+2x$の最大値問題の解法について「①平方完成に基づく方法」と「②微分に基づく方法」についてそれぞれ確認を行う。まず①の平方完成については下記のように式変形を行うことができる。
$$
\large
\begin{align}
f(x) &= -x^2 + 2x \\
&= -(x^2-2x) \\
&= -(x^2-1)^2 + 1
\end{align}
$$
上記より関数$f(x)=-x^2+2x$は$x=1$のときに最大値$1$を取ることが確認できる。平方完成については下記でも詳しく取り扱った。
②の微分に基づく方法では、「導関数$f'(x)$が関数$f(x)$の傾きに対応する」ことに基づいて増減表を作成し、最大値における$x$を導出する。まず関数$f(x)$の微分は下記のように計算できる。
$$
\large
\begin{align}
f'(x) &= -2x + 2 \\
&= -2(x-1)
\end{align}
$$
上記より、$x<1$では$f'(x)>0$、$x>1$では$f'(x)<0$、$x=1$では$f'(x)=0$であることが確認できる。よって、下記のように関数$f(x)$の増減表を作成することができる。
$$
\large
\begin{array}{|c|*3{c|}}\hline x & \cdots & 1 & \cdots \\
\hline f'(x) & + & 0 & – \\
\hline f(x) & \nearrow & \displaystyle \max & \searrow \\
\hline
\end{array}
$$
増減表より関数$f(x)=-x^2+2x$は$x=1$のときに最大値$1$を取ることが確認できる。
当項で確認したように、微分を元に増減表を作成することで最大値・最小値問題の解を得ることができる。①の平方完成の方法では$2$次関数以外では適用できない場合が多いが、微分に基づく手法は多くの関数に対し汎用的に用いることができるなど大変有用である。