当記事では「統計学を学ぶにあたって最低限抑えておきたい数学」の中から「$1$次関数・$2$次関数とその応用」に関して取り扱います。特に平方完成がよく出てくる一方で計算が複雑になることが多いので、具体的な応用事例なども合わせて取り扱いました。
取りまとめにあたっては数学の解説に関してはなるべくシンプルに取り扱いますが、統計学への応用に関連した複雑な内容に関しては目次に「*」をつけました。「*」がついているものはやや難しいので、読み飛ばしても問題ありません。
・基本数学まとめ
https://www.hello-statisticians.com/math_basic
Contents
$1$次関数
$1$次関数の概要
$f(x) = ax + b$で表される関数を$1$次関数といいます。また、$a$は傾き、$b$は切片などと呼ばれます。$1$次関数を理解するにあたってはグラフの描画を行うとわかりやすいです。以下、Pythonを用いてグラフの描画を行います。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-2,3,1)
a, b = np.array([1,1,2,-1]), np.array([1,0,0,1])
for i in range(a.shape[0]):
y = a[i]*x+b[i]
plt.subplot(2,2,i+1)
plt.title("a={}, b={}".format(a[i],b[i]))
plt.plot(x,y)
plt.scatter(x,y)
plt.plot(np.array([0,0]),np.array([-3*np.abs(a[i])+b[i],b[i]]),"k--")
plt.plot(np.array([-3,0]),np.array([b[i],b[i]]),"k--")
plt.show()・実行結果
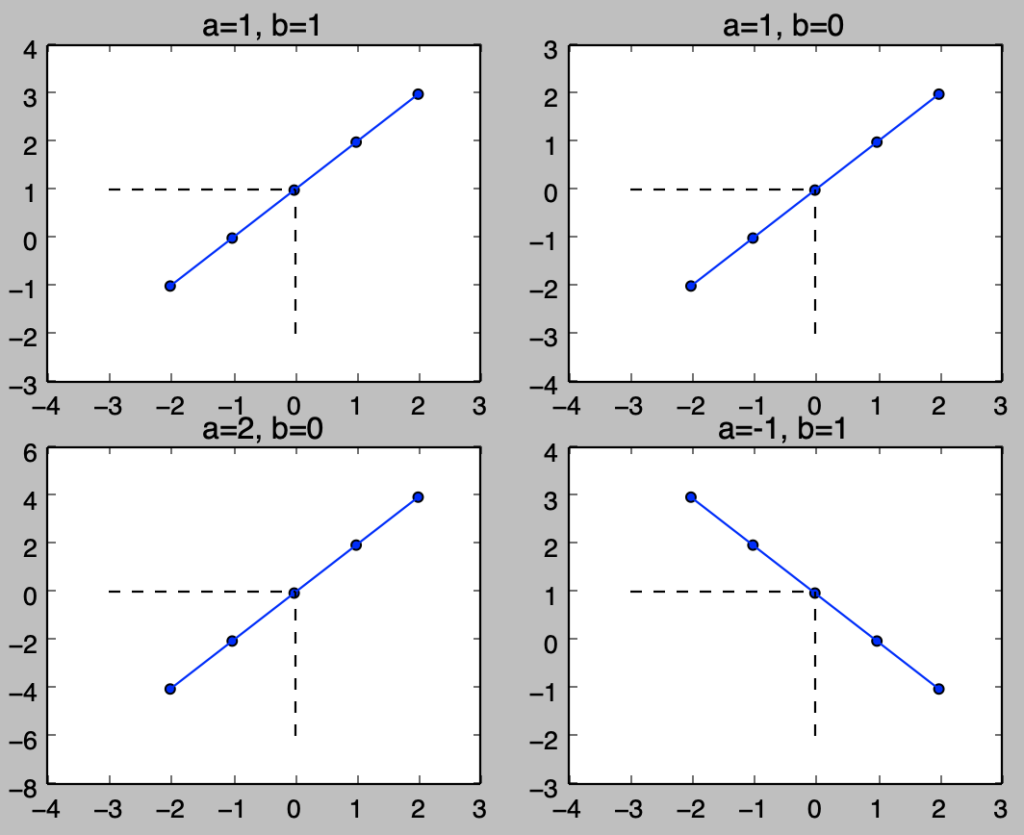
回帰
$2$次関数
$2$次関数の概要
$f(x)=ax^2+bx+c,a \neq 0$で表される関数を$2$次関数といいます。$f(x)=ax^2+bx+c$は次項で取り扱う平方完成の考え方を用いることで$a(x-p)^2+q$の式に変形できることから、以下当項では$f(x)=ax^2$のみを取り扱います。
$1$次関数と同様にグラフで確認するとわかりやすいので、下記では$a=1,2,-1,2$に対してそれぞれPythonを用いて$f(x)=ax^2$の描画を行います。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-2,3,1)
x_ = np.arange(-2,2.01,0.01)
a = np.array([1,2,-1,-2])
for i in range(a.shape[0]):
y, y_ = a[i]*x**2, a[i]*x_**2
plt.subplot(2,2,i+1)
plt.title("a={}".format(a[i]))
plt.plot(x_,y_)
plt.scatter(x,y)
plt.show()・実行結果
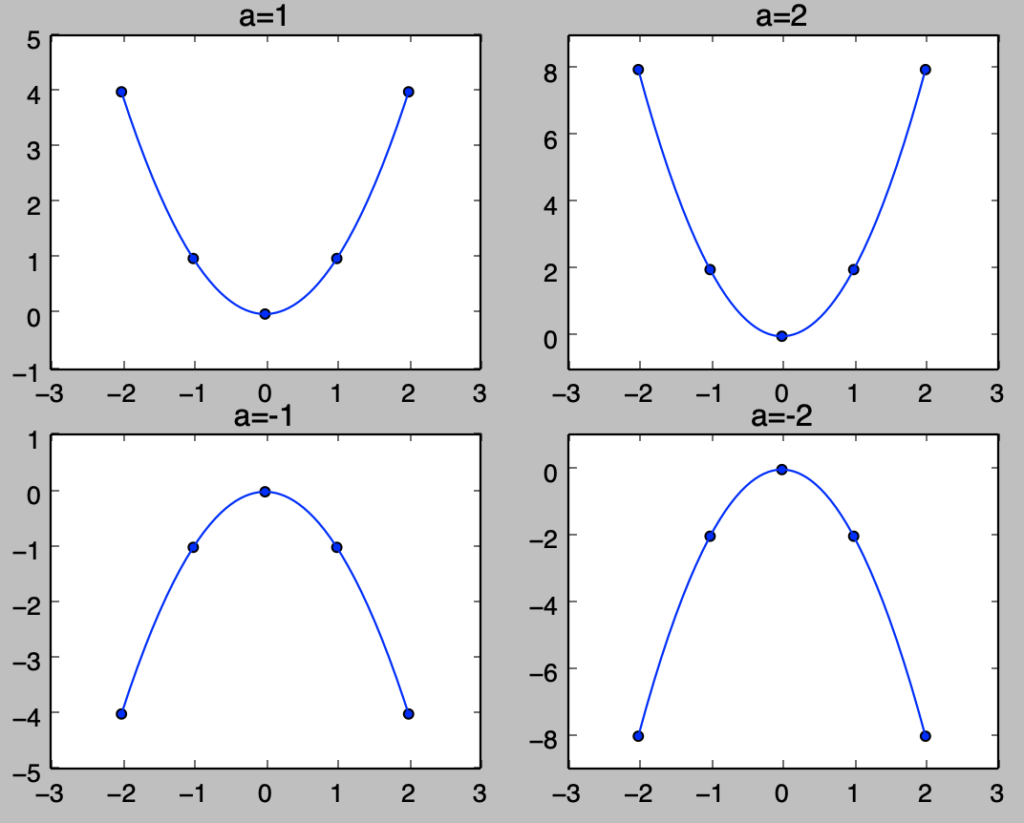
平方完成の概要
$f(x)=a(x-p)^2+q$は$f(x)=ax^2$を$x$方向に$p$、$y$方向に$q$平行移動させた関数です。式だけではわかりにくいので、前項の$a=1,2,-1,2$に対応する$f(x)=ax^2$に対し、$f(x)=a(x-1)^2+2$を描画することで$x$方向に$1$、$y$方向に$2$平行移動することを確認します。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-1,4,1)
x_ = np.arange(-1,3.01,0.01)
a = np.array([1,2,-1,-2])
for i in range(a.shape[0]):
y, y_ = a[i]*(x-1)**2+2, a[i]*(x_-1)**2+2
plt.subplot(2,2,i+1)
plt.title("a={}".format(a[i]))
plt.plot(x_,y_)
plt.scatter(x,y)
plt.show()・実行結果
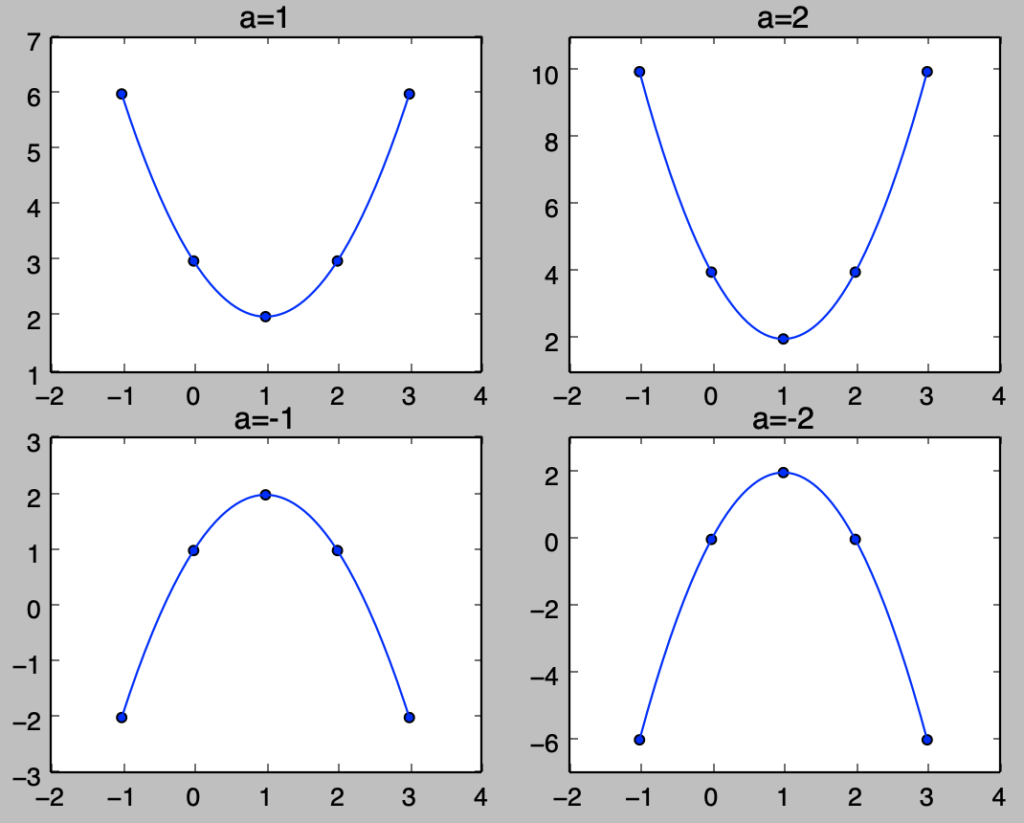
上記よりグラフが$x$方向に$1$、$y$方向に$2$平行移動されたことが確認できます。このことに基づいて$f(x)=ax^2+bx+c$を$f(x)=a(x-p)^2+q$に変形することで$f(x)=ax^2$の平行移動であると考えることができます。
このとき$f(x)=ax^2+bx+c$を$f(x)=a(x-p)^2+q$に式変形することを「平方完成」といいます。$f(x)=ax^2+bx+c$の平方完成の方法に関しては次項で取り扱います。
$f(x)=ax^2+bx+c$の平方完成
$f(x)=ax^2+bx+c$の平方完成は下記のように行うことができます。
$$
\large
\begin{align}
f(x) &= ax^2 + bx + c \\
&= a \left( x^2 + \frac{b}{a}x \right) + c \\
&= a \left( x^2 + 2 \times \frac{b}{2a}x + \left(\frac{b}{2a}\right)^2 – \left(\frac{b}{2a}\right)^2 \right) + c \\
&= a \left( x^2 + 2 \times \frac{b}{2a}x + \left(\frac{b}{2a}\right)^2 \right) + c – a \left(\frac{b}{2a}\right)^2 \\
&= a \left( x + \frac{b}{2a} \right)^2 + c – \frac{b^2}{4a}
\end{align}
$$
上記はなるべく変形がわかりやすいように丁寧に式変形を行いましたので、実際に行う場合は適宜省略して計算を行うと良いと思います。
平方完成を行う際の計算の簡略化のコツ*
平方完成を行うにあたって、前項のようにストレートな方法で計算を行う方法もありますが、複雑な計算になる場合も多いことから「$f(x)=a(x-p)^2+q$の展開式を元に公式のように理解する」という考え方も重要であるというのが筆者の見解です。
$f(x)=a(x-p)^2+q$の展開は下記のように行うことができます。
$$
\large
\begin{align}
f(x) &= a(x-p)^2 + q \\
&= a(x^2-2px+p^2) + q \\
&= ax^2 – 2apx + ap^2 + q
\end{align}
$$
上記を$f(x)=ax^2+bx+c$に対応させるにあたって、$p,q$を$a,b,c$を用いて表すことを考えます。
$$
\large
\begin{align}
-2ap &= b \\
p &= – \frac{b}{2a} \\
ap^2 + q &= c \\
q &= c – a \times \left( – \frac{b}{2a} \right) \\
&= c – \frac{ab}{4a^2} = c – \frac{b}{4a}
\end{align}
$$
上記の計算は前項で取り扱った計算とそれほど違いがあるように見えませんが、$f(x)=ax^2+bx+c$が$\displaystyle – \frac{1}{2 \sigma^2} \left( N \mu^2 – 2 N \mu_{ML} \mu + \sum_{n=1}^{N} x_n^2 \right) – \frac{(\mu-\mu_{0})^2}{2 \sigma_{0}^{2}}$を$\mu$に関して平方完成を行う場合などのように複雑な計算を直接的に計算するのはなかなか大変です。よって、ここで考えたように$p,q$を$a,b,c$で表した上で代入するという考え方も抑えておくと良いと思います。
また、定数項の$\displaystyle q = c – \frac{b^2}{4a}$が考察に必要ない際は、具体的な計算を行わないで$\mathrm{Const.}$のように表す場合もあることは抑えておくと良いです。たとえば$\displaystyle – \frac{1}{2 \sigma^2} \left( N \mu^2 – 2 N \mu_{ML} \mu + \sum_{n=1}^{N} x_n^2 \right) – \frac{(\mu-\mu_{0})^2}{2 \sigma_{0}^{2}}$などの計算を通して「正規分布」における「事後分布の導出」を行う際などは、$(\mu-\mu_N)^2$の$\mu_N$がわかればよく、定数項は$\mathrm{Const.}$を用いて計算を行わない場合が多いです。
正規分布の事後分布と平方完成*
正規分布に対してベイズ法を用いて「事前分布」と「観測されたサンプル」から「事後分布」を導出する際に平方完成の考え方を用います。「事前分布」を$p(\mu_{0},\sigma_{0}^2)$、「サンプルが観測される確率」を$p(x_1,…,x_n|\mu,\sigma^2)$とするとき、それぞれ下記のように式で表せます。
$$
\large
\begin{align}
p(\mu_{0},\sigma_{0}^2) &= \frac{1}{\sqrt{2 \pi \sigma_0^2}} \exp \left( -\frac{(x-\mu_0)^2}{2 \sigma_0^2} \right) \\
p(x_1,…,x_n|\mu,\sigma^2) &= \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(x_i-\mu)^2}{2 \sigma^2} \right)
\end{align}
$$
