当記事は「倉田+, 入門統計解析 (新世社)」の読解サポートにあたって5章「独立同一分布」の演習問題を解説します。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。(そのため著者の意図とは異なる解説となる可能性はあります)
演習問題解答例
5.1 多次元確率分布
5.1.1
(1) まず$X$の周辺分布$P(X=-1)$,$P(X=0)$,$P(X=1)$をそれぞれ求める.
表を横方向に足し合わせれば良い(行和)ので,
$P(X=-1) = 0.3$,$P(X=0) = 0.4$,$P(X=1) = 0.3$
である.したがって,$X$の期待値$E(X)$は
$$
E(X) = -1\times 0.3 + 0\times 0.4 + 1\times 0.3=0
$$
である.また,分散$V(X)$は
$$V(X) = E(X^2) – E(X)^2 = (-1)^2\times 0.3 + 0^2\times 0.4 + 1^2\times 0.3 – 0^2 = 0.6$$
(2) $Y$については表を縦方向に足し合わせる(列和).したがって,
$P(Y=-1) = 0.4$,$P(Y=0) = 0.2$,$P(Y=1) = 0.4$
であるから,期待値$E(Y)$は
$$E(Y) = -1\times 0.4 + 0\times 0.2 + 1\times 0.4 = 0$$
である.また分散$V(Y)$は
$$V(Y) = E(Y^2)-E(Y)^2 = (-1)^2\times 0.4 + 0^2 \times 0.2+ 1^2\times 0.4 – 0^2 = 0.8$$
である.
(3) $C(X,Y) = E(XY) – E(X)E(Y)$であるから,$E(XY)$を計算する.
$X$,$Y$はどちらも$-1,0,1$のいずれかの値をとるので,$XY$は$(-1)\times (-1), (-1)\times 0, (-1)\times 1, 0\times(-1), 0\times 0, 0\times 1, 1\times(-1), 1\times 0, 1\times1$のいずれかとなる.
それぞれの確率は表からわかるのでそれを用いて期待値$E(XY)$を計算すると,
$$
\begin{align*}
E(XY) &=& (-1)&\cdot(-1)\cdot 0.1 &+ (-1)&\cdot 0 \cdot 0.1 &+ (-1)&\cdot 1 \cdot 0.1 \\
& &+0&\cdot(-1)\cdot 0.2 &+ 0&\cdot 0 \cdot 0 &+ 0&\cdot 1 \cdot 0.2 \\
& &+1&\cdot(-1)\cdot 0.1 &+ 1&\cdot 0 \cdot 0.1 &+ 1&\cdot 1 \cdot 0.1 \\
&= 0
\end{align*}
$$
となる.したがって,共分散$C(X,Y)$は
$$C(X,Y) = E(XY)- E(X)E(Y) = 0 – 0 = 0$$
また,${\displaystyle \rho_{XY} = \frac{C(X,Y)}{\sqrt{V(X)}\sqrt{V(Y)}} = 0}$.
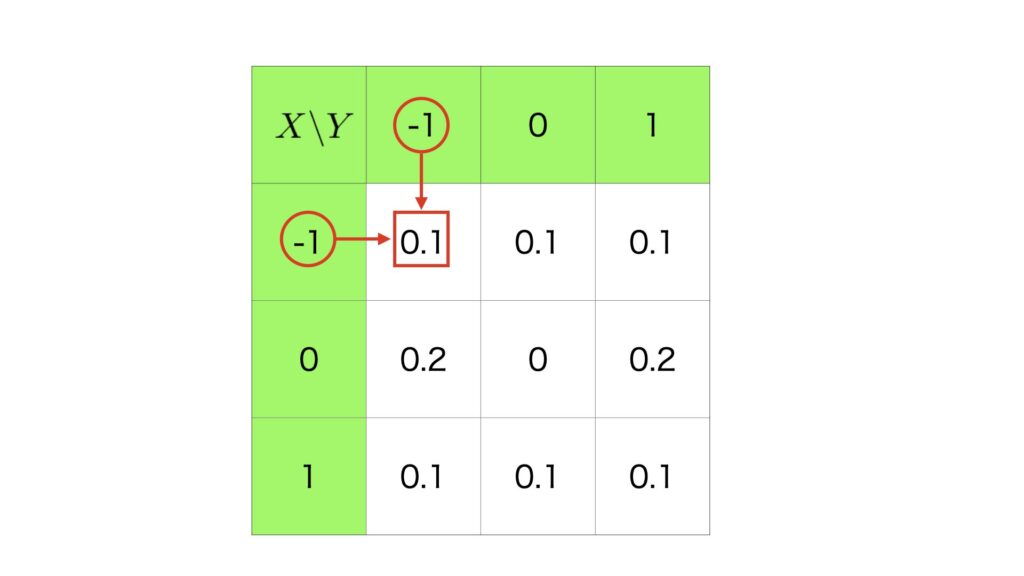
これを表の$9$箇所の値について計算して,その和をとれば$E(XY)$を求めることができる.
5.1.2
(1) $X$の周辺分布は横方向に和をとれば良い(行和).
$$ P(X = 0) = \frac{8}{20} , P(X=1) = \frac{4}{20} , P(X=2) = \frac{8}{20} $$
$Y$の周辺分布は縦方向に和をとれば良い(列和).
$$ P(Y=1) = \frac{8}{20} , P(Y=2) = \frac{4}{20} , P(Y=3) = \frac{8}{20} $$
(2) $E(X)$は(1)の結果を用いて計算すると,$E(X) = 1$.
また,${\displaystyle E(X^2)=\frac{9}{5} } $ であるから
$$ V(X) = E(X^2) – E(X)^2 = \frac{9}{5} – 1^2 = \frac{4}{5} $$
となる.
(3) $C(XY) = E(XY) – E(X)E(Y)$であるから,$E(XY)$と$E(Y)$を求める.
$E(XY)$はさきほどの$5.1.1$と同様に表から計算すればよく,その値は$E(XY) = 2$,$ E(Y) = 2$であるから,
$$ C(X,Y) = E(XY)-E(X)E(Y) = 2-1\cdot 2 = 0 $$
である.
(4) 各$x,y$に対して$P(X=x,Y=y) = P(X=x)P(Y=y)$が成り立つとき$X$と$Y$は独立であるという(テキストでは5.2節に定義の記載がある).
しかし,例えば$P(X=1,Y=2) = 0$,${\displaystyle P(X=1) = \frac{4}{20}}$,${\displaystyle P(Y=2) = \frac{2}{10}}$であり,$P(X=1,Y=2) \neq P(X=1)P(Y=2)$であるから,$X$と$Y$は独立ではない.
5.1.3
(1) 5.1.1と同様に$X$の周辺分布は$P(X=1)=0.3$,$P(X=2)=0.3$,$P(X=3) = 0.4$.
したがって,期待値$E(X)$は$E(X)=2.10$である.
また,$E(X^2) = 5.10$であるから,分散$V(X)$は$V(X) = E(X^2)-E(X)^2 = 5.10-4.41 = 0.69$.
(2) $Y$も同様に計算すればよい.
$Y$の周辺分布は$P(Y=90)=0.09$,$P(Y=100)=0.28$,$P(Y=110) = 0.28$,$P(Y=120) = 0.26$,$P(Y=130) = 0.09$.
したがって,期待値$E(Y)$は$E(Y) = 109.8$.
また,$E(Y^2) = 12182.0$であるから,分散$V(Y)$は$V(Y) = E(Y^2)-E(Y)^2 = 12182.0-12056.0 = 125.9$.
(3) 共分散$C(X,Y)$は$C(X,Y) = E(XY)-E(X)E(Y)$で求めることができる.
$E(XY)$は,やはり$5.1.1$と同様に,各$XY$の値とその確率が表から直ちにわかり,その値は$E(XY) = 236.4$である.
したがって,
$$ C(X,Y) = E(XY)-E(X)E(Y) = 236.4 – 230.58 = 5.82 $$
となる.
また,${\displaystyle\rho_{XY} = \frac{C(X,Y)}{\sqrt{V(X)}\sqrt{V(Y)}} }$なので,
$$ \rho_{XY} = \frac{5.82}{\sqrt{0.69}\sqrt{125.9}} = 0.62. $$
5.1.4
(1) ${\displaystyle P(Y=y|X=90) = \frac{P(Y=y,X=90)}{P(X=90)}}$である.
したがって,
$$ P(Y=250|X=90) = \frac{0.1}{0.7} = 0.14$$
$$ P(Y=300|X=90) = \frac{0.2}{0.7} = 0.29$$
$$ P(Y=350|X=90) = \frac{0.4}{0.7} = 0.57$$
となる.
(2) $(1)$の結果を用いて計算する.
$${\displaystyle E(Y=y|X=90) = 250\cdot\frac{1}{7} + 300\cdot \frac{2}{7} + 350\cdot \frac{4}{7} = 321.4}$$
(3) $(1)$における$X=90$を$X=110$として計算すればよい.
\[ P(Y=250|X=110) = \frac{0.1}{0.3} = 0.33\]
\[ P(Y=300|X=110) = \frac{0.1}{0.3} = 0.33\]
\[ P(Y=350|X=110) = \frac{0.1}{0.3} = 0.33\]
(4) $(2)$と同様.
${\displaystyle E(Y=y|X=110) = 250\cdot\frac{1}{3} + 300\cdot \frac{1}{3} + 350\cdot \frac{1}{3} = 300.0}$
5.1.5
(1) $i$を任意に$1$つ固定して考える.結果$C_i$が起こる確率が$p_i$なので,$C_i$以外の結果が起こることをまとめて$1$つの結果だと考えると,その確率は$1-p_i$である.これは成功確率$p_i$,長さ$n$のベルヌーイ試行とみなすことができる.
よって,$X_i$は二項分布$B(n,p_i)$に従う.したがって,$E(X_i)=np_i$である.
(ここで,$B(n,p)$の期待値は$np$であることを用いた.)
(2) $(1)$と同様に,二項分布$B(n,p_i)$の分散が$np(1-p)$であることを利用すると,$V(X)=np_i(1-p_i)$とわかる.
(3) $C(X_i,X_j) = E(X_iX_j)-E(X_i)E(X_j)$を利用する.$E(X_i)$,$E(X_j)$は$(1)$からわかるので,$E(X_iX_j)$を計算する.
$X_i=n_i$かつ$X_j=n_j$となる確率は
\[
P(X_i=n_i,X_j=n_j) = \frac{n!}{n_i!n_j!(n-n_i-n_j)!}p_i^{n_i}p_j^{n_j}(1-p_i-p_j)^{n-n_i-n_j}
\]
である.従って,$E(X_iX_j)$は
$$
\begin{align*}
&E(X_iX_j)\\
&= \sum_{\substack{ 1\leq n_i,n_j \leq n \\ n_i + n_j \leq n}} n_i n_j
\frac{n!}{n_i!n_j!(n-n_i-n_j)!}p_i^{n_i}p_j^{n_j}(1-p_i-p_j)^{n-n_i-n_j} \\
&=n(n-1)p_ip_j \times\\
& \quad \sum_{\substack{ 1\leq n_i,n_j \leq n \\ n_i + n_j \leq n}} \frac{(n-2)!}{(n_i-1)!(n_j-1)!(n-n_i-n_j)!}p_i^{n_i-1}p_j^{n_j-1}(1-p_i-p_j)^{n-n_i-n_j} \\
&= n(n-1)p_ip_j(p_i+p_j+(1-p_i-p_j))^{n-2}\\
&= n(n-1)p_ip_j
\end{align*}
$$
となる(ここで$3$行目から$4$行目の式変形には多項定理を利用した).以上から
$$
\begin{align*}
C(X_i,X_j) &= E(X_iX_j)-E(X_i)E(X_j)\\
&= n(n-1)p_ip_j – np_i \cdot np_j\\
&= -np_ip_j
\end{align*}
$$
となる.
(補足)多項定理
$(a+b+c)^n$の展開式における$a^p b^q c^r$の項の係数は${\displaystyle \frac{n!}{p!q!r!}}$である.ただし,$p+q+r = n $.
これを利用すると
\[
(a+b+c)^n = \sum_{\substack{0\leq p,q,r \leq n \\ p+q+r=n}}\frac{n!}{p!q!r!}a^p b^q c^r
\]
とわかる.
従って,$a = p_i$,$b = p_j$,$c = 1 – p_i – q_j$とし,また$n-2 = n + (n_i-1) + (n_j-1)$と考えて多項定理を適用すればよい.
