当記事は「統計学実践ワークブック(学術図書出版社)」の読解サポートにあたってChapter.8の「統計的推定の基礎」に関して演習問題を中心に解説を行います。統計量、推定量、推定値などは少々紛らわしいですが、概念を掴むと全体の理解がしやすくなるので演習を通して抑えておくと良いと思います。
Contents
本章のまとめ
有効推定量とクラメル・ラオの不等式
代表値を表すパラメータ$\theta$に基づいて標本$x_1,x_2,…,x_n$が得られたと考える。このとき代表値の推定量を表す標本の関数の統計量を$\hat{\theta} = T(x_1,x_2,…,x_n)$、$\hat{\theta}$の分散を$V[\hat{\theta}]$を下記のように表す。
$$
\large
\begin{align}
V[\hat{\theta}] &= V[T(X_1,X_2,…,X_n)] \\
&= V \left[ \frac{1}{n} \sum_{i=1}^{n} X_i \right] \\
&= \frac{1}{n^2} \times n V[X_i] = \frac{1}{n} V[X_i]
\end{align}
$$
また、下記のようにパラメータ$\theta$に関する尤度を$L(\theta)$とおく。
$$
\large
\begin{align}
L(\theta) &= P(X_1=x_1,X_2=x_2,…,X_n=x_n|\theta) \\
&= \prod_{i=1}^{n} P(X_i=x_i|\theta)
\end{align}
$$
上記に対し、対数尤度を$l(\theta) = \log{L(\theta)}$のようにおく。さらに対数尤度を元に$\theta$に関するフィッシャー情報量を下記のようにおく。
$$
\large
\begin{align}
I_{n}(\theta) = – E \left[ \frac{\partial^2}{\partial \theta^2} l(\theta) \right]
\end{align}
$$
このとき、下記で表すクラメル・ラオの不等式が$V[\hat{\theta}]$と$I_{n}(\theta)$に関して成立する。
$$
\large
\begin{align}
V[\hat{\theta}] \geq I_{n}(\theta)^{-1}
\end{align}
$$
また、上記で等号が成立するとき、$\hat{\theta}$を有効推定量(efficient estimator)と呼ぶ。有効推定量が一様最小分散不偏推定量であることも抑えておくと良い。
クラメル・ラオの不等式の取り扱いに関しては数式だけだと分かりにくいので一連の流れを下図にまとめた。
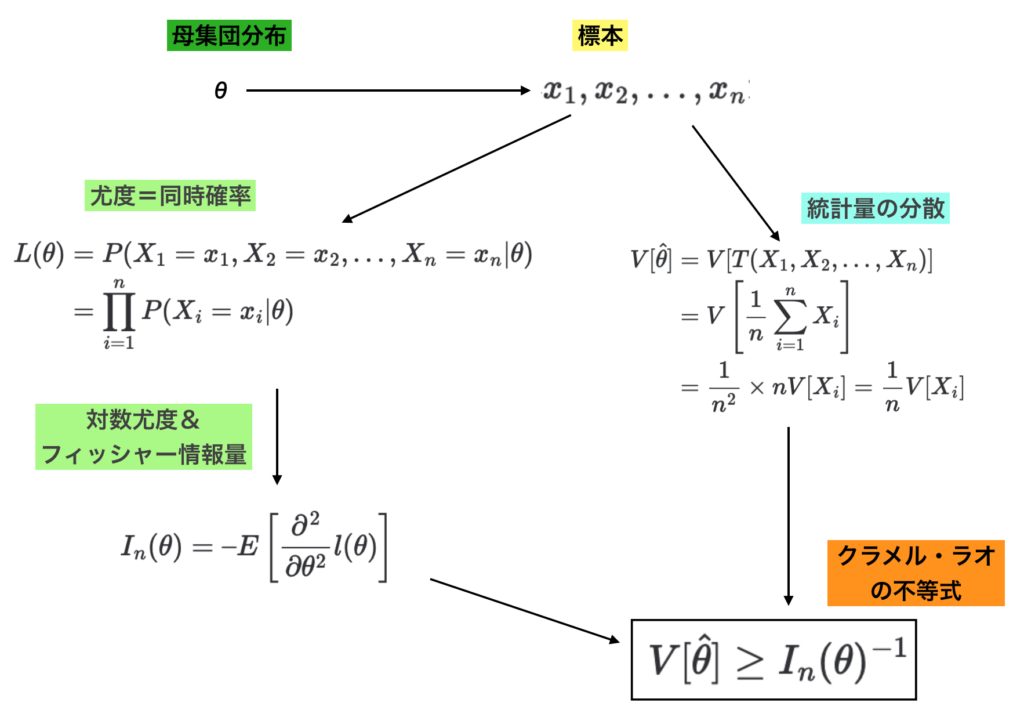
ここではわかりやすさの観点から$\theta$を正規分布の$\mu$やポアソン分布の$\lambda$に対応する代表値に限った議論を行なったが、代表値以外のパラメータも$\theta$で総称されるかつ代表値以外のパラメータでも同様の議論が成立することは抑えておくと良い。
漸近有効性・漸近正規性
パラメータ$\theta$に対して推定量$\hat{\theta}$を考えるとき、下記が成立するならば推定量$\hat{\theta}$は漸近有効性(asymptotic efficiency)を持つという。
$$
\large
\begin{align}
\lim_{n \to \infty} n V[\hat{\theta}] = J_{1}(\theta)^{-1}
\end{align}
$$
上記の数式はクラメル・ラオの不等式の統合が成立するときの$V[\hat{\theta}] = I_{n}(\theta)^{-1}$に類似した式である一方で、$J_{n}(\theta)^{-1}$ではなく$J_{1}(\theta)^{-1}$が用いられる分左辺に$n$がかけられていることは抑えておくと良い。
また、最尤推定量$\hat{\theta}$は漸近有効性をもちかつ、パラメータ$\theta$を$\hat{\theta}$から引いた$\hat{\theta}-\theta$を$\sqrt{n}$でスケーリングした$Z:=\sqrt{n}(\hat{\theta}-\theta)$は正規分布$N(0,J_{1}(\theta)^{-1})$に分布収束する。
このことを最尤推定量の漸近正規性(asymptotic normality)という。
ジャックナイフ推定量
推定量が不偏ではなくバイアスがある場合、標本を「再活用」して推定量のバイアスを補正する方法をジャックナイフ法(jackknife method)という。標本$X_1,…,X_n$から標本$X_{i}$を除いた部分標本を元に得られる推定量を$\hat{\theta}_{(i)}$とおく。
このとき下記のように$\hat{\theta}_{(i)}$の平均$\hat{\theta}_{(\cdot)}$を定義する。
$$
\large
\begin{align}
\hat{\theta}_{(\cdot)} = \frac{1}{n} \sum_{i=1}^{n} \hat{\theta}_{(i)}
\end{align}
$$
上記のように定めた$\hat{\theta}_{(\cdot)}$を元に推定量$\hat{\theta}$のバイアス$\hat{\mathrm{bias}}$は下記のように見積もられる。
$$
\large
\begin{align}
\hat{\mathrm{bias}} = (n-1)(\hat{\theta}_{(\cdot)}-\hat{\theta})
\end{align}
$$
また、$\hat{\mathrm{bias}}$を用いて$\hat{\theta}$の補正を行なったジャックナイフ推定量$\hat{\theta}_{jack}$は下記のように定められる。
$$
\large
\begin{align}
\hat{\theta}_{jack} = \hat{\theta} – \hat{\mathrm{bias}}
\end{align}
$$
演習問題解説
例8.1
統計量は未知のパラメータ$\theta$によらない標本の関数であるので、$\displaystyle \frac{1}{n} \sum_{i=1}^{n}(X_i-\mu)^2$以外は統計量である。
例8.2
尤度関数を$L(\mu,v)$と定めると、同時確率密度関数に一致することより、下記のように表すことができる。
$$
\large
\begin{align}
L(\mu,v) &= \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi v}} \exp \left[ -\frac{(x_i-\mu)^2}{2v} \right] \\
&= \left( \frac{1}{\sqrt{2 \pi v}} \right)^n \prod_{i=1}^{n} \exp \left[ -\frac{(x_i-\mu)^2}{2v} \right] \\
&= \left( \frac{1}{\sqrt{2 \pi v}} \right)^n \exp \left[ \sum_{i=1}^{n} -\frac{(x_i-\mu)^2}{2v} \right]
\end{align}
$$
このとき、対数尤度関数を$l(\mu,v)$と定めると、$l(\mu,v)=\log{L(\mu,v)}$より、下記のように表せる。
$$
\large
\begin{align}
l(\mu,v) &= \log{L(\mu,v)} \\
&= -\frac{n}{2} \log{(2 \pi v)} + \sum_{i=1}^{n} \left( -\frac{(x_i-\mu)^2}{2v} \right) \\
&= -\frac{n}{2} \log{(2 \pi v)} – \frac{1}{2v} \sum_{i=1}^{n} (x_i-\mu)^2
\end{align}
$$
ここで対数尤度$l(\mu,v)$の$\mu$に関する偏微分を考える。
$$
\large
\begin{align}
\frac{\partial l(\mu,v)}{\partial \mu} &= \frac{1}{2v} \sum_{i=1}^{n} 2(x_i-\mu) \\
&= \frac{1}{v} \sum_{i=1}^{n} (x_i-\mu) \\
&= \frac{n(\bar{x}-\mu)}{v}
\end{align}
$$
上記より、$v>0$の場合$v$の値に関わらず、$\mu=\bar{x}$のとき$l(\mu,v)$が最大となることがわかる。よって、$\mu$の最尤推定量は$\bar{x}$に一致する。
次に$\mu=\bar{x}$を元に$l(\bar{x},v)$の$v$に関する最大値を考える。$l(\bar{x},v)$を$v$に関して偏微分を行うと、標本分散を$\displaystyle S = \frac{1}{n} \sum_{i=1}^{n} (x_i-\bar{x})^2$とおいて、下記のように計算できる。
$$
\large
\begin{align}
\frac{\partial l(\bar{x},v)}{\partial v} &= \frac{\partial}{\partial v} \left( -\frac{n}{2} \log{(2 \pi v)} – \frac{1}{2v} \sum_{i=1}^{n} (x_i-\bar{x})^2 \right) \\
&= \frac{\partial}{\partial v} \left( -\frac{n}{2} \log{(2 \pi v)} – \frac{nS}{2v} \right) \\
&= -\frac{n \times 2 \pi}{2 \times 2 \pi v} + \frac{nS}{2v^2} \\
&= -\frac{n}{2v} + \frac{nS}{2v^2} \\
&= \frac{n}{2v} \left( \frac{S}{v}-1 \right)
\end{align}
$$
上記より、$v=S$のとき$l(\bar{x},v)$は最大値をとることがわかる。よって、標本分散$\displaystyle S = \frac{1}{n} \sum_{i=1}^{n} (x_i-\bar{x})^2$が$v$の最尤推定量であることがわかる。
以上の議論により、$\mu, v$の最尤推定量は標本平均$\displaystyle \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$と標本分散$\displaystyle S = \frac{1}{n} \sum_{i=1}^{n} (x_i-\bar{x})^2$であると考えることができる。
例8.3
ガンマ分布$Ga(\alpha,1/\lambda)$の期待値$\mu_1=E[X]$と分散$\mu_2=V[X]$はそれぞれ$\mu_1=E[X]=\alpha/\lambda$、$\mu_2=V[X]=\alpha/\lambda^2$である。これを$\alpha, \lambda$に関して解くと下記が得られる。
$$
\large
\begin{align}
\alpha &= \frac{\mu_1^2}{\mu_2} \\
\lambda &= \frac{\mu_1}{\mu_2}
\end{align}
$$
また、モーメント法では$\mu_1, \mu_2$の推定量に標本平均$\bar{X}$と標本分散$S$を用いて推定を行うと考えられる。よって、$\alpha$と$\lambda$の推定量$\hat{\alpha}, \hat{\lambda}$は下記のように表すことができる。
$$
\large
\begin{align}
\hat{\alpha} &= \frac{\bar{X}^2}{S} \\
\lambda &= \frac{\bar{X}}{S}
\end{align}
$$
・参考
ガンマ分布のモーメント母関数の導出と期待値・分散の計算
https://www.hello-statisticians.com/explain-terms-cat/gamma_distribution1.html
例8.4
$x_1,x_2,…,x_n$に関する同時確率密度関数の式を$f(x_1,…,x_n|\mu,\sigma^2)$とおくと、$f(x_1,…,x_n|\mu,\sigma^2)$の式は下記のように分解することができる。
$$
\large
\begin{align}
f(x_1,…,x_n|\mu,\sigma^2) &= \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( – \frac{(x_i-\mu)^2}{2 \sigma^2} \right) \\
&= (2 \pi \sigma^2)^{-n/2} \exp \left( – \sum_{i=1}^{n} \frac{((x_i-\bar{x})+(\bar{x}-\mu))^2}{2 \sigma^2} \right) \\
&= (2 \pi \sigma^2)^{-n/2} \exp \left( – \sum_{i=1}^{n} \frac{(x_i-\bar{x})^2}{2 \sigma^2} \right) \exp \left( – \sum_{i=1}^{n} \frac{(\bar{x}-\mu)^2}{2 \sigma^2} \right)
\end{align}
$$
上記にフィッシャーネイマンの分解定理を適用することで、$\left( \bar{x} , \sum_{i=1}^{n}(x_i-\bar{x})^2 \right)$が十分統計量であることがわかる。
・参考
十分統計量の定義・分解定理と証明の具体例
https://www.hello-statisticians.com/explain-terms-cat/sufficient_statistic1.html
問8.1
①、②、④が正しい。以下詳しく確認を行う。
① 正しい:統計量は標本もしくは既知のパラメータの関数で表されなければならない。
② 正しい:尤度関数における積は順序を入れ替えることができるので十分統計量であると考えることができる。
③ 正しくない:$\sigma^2$の不偏推定量には$\displaystyle \frac{1}{n-1} \sum_{i=1}^{n}(X_i-\bar{X})^2$が対応する。
④ 正しい:正規分布の標本分散は分散の最尤推定量である。母分散の推定量は不偏推定量と最尤推定量が異なることは抑えておくと良い。
⑤ 正しくない:標本分散は一致推定量かつ漸近有効推定量である。
問8.2
$[1]$
尤度関数を$L(\lambda)$とおくと、$L(\lambda)$は同時確率関数$f(X_1=x_1,…,X_n=x_n)$に一致することから下記のように表すことができる。
$$
\large
\begin{align}
L(\lambda) &= f(X_1=x_1,…,X_n=x_n) = \prod_{i=1}^{n} f(X_i=x_i) \\
&= \prod_{i=1}^{n} \frac{\lambda^{x_i} e^{-\lambda}}{x_i!}
\end{align}
$$
上記の対数尤度$\log{L(\lambda)}$は下記のように表せる。
$$
\large
\begin{align}
\log{L(\lambda)} = \sum_{i=1}^{n} x_i \log{\lambda} – n \lambda + \sum_{i=1}^{n} \log{x_i!}
\end{align}
$$
上記を$\lambda$で偏微分すると下記のようになる。
$$
\large
\begin{align}
\frac{\partial \log{L(\lambda)}}{\partial \lambda} = \frac{1}{\lambda} \sum_{i=1}^{n} x_i – n
\end{align}
$$
ここで$\lambda>0$において上記は$\lambda$に対して単調減少であるので$\displaystyle \frac{\partial \log{L(\lambda)}}{\partial \lambda} = 0$となる$\lambda$が対数尤度$\log{L(\lambda)}$を最大にする$\lambda$であることがわかる。
$$
\large
\begin{align}
\frac{\partial \log{L(\lambda)}}{\partial \lambda} &= 0 \\
\frac{1}{\lambda} \sum_{i=1}^{n} x_i – n &= 0 \\
\lambda = \frac{1}{n} \sum_{i=1}^{n} x_i
\end{align}
$$
上記より$\displaystyle \hat{\lambda} = \frac{1}{n} \sum_{i=1}^{n} x_i$が$\lambda$の最尤推定量であり、式より標本平均に一致することも合わせて確認できる。
$[2]$
$\lambda$に関するフィッシャー情報量を$J_{n}(\lambda)$とおくと、$J_{n}(\lambda)$は下記のように計算することができる。
$$
\large
\begin{align}
J_{n}(\lambda) &= – E \left[ \frac{\partial^2}{\partial \lambda^2} \log{L(\lambda)} \right] \\
&= – E \left[ \frac{\partial}{\partial \lambda} \left( \frac{1}{\lambda} \sum_{i=1}^{n} X_i – n \right) \right] \\
&= – E \left[ – \frac{1}{\lambda^2} \sum_{i=1}^{n} X_i \right] \\
&= \frac{n}{\lambda^2} E[X] \\
&= \frac{n}{\lambda^2} \lambda = \frac{n}{\lambda}
\end{align}
$$
$[3]$
$[1]$より$\lambda$の最尤推定量は標本平均であると考えることができる。ここで標本平均の分散$V[\bar{X}]$は下記のように表すことができる。
$$
\large
\begin{align}
V[\bar{X}] &= V \left[ \frac{1}{n} \sum_{i=1}^{n} X_i \right] \\
&= \frac{1}{n^2} \times n V[X] \\
&= \frac{\lambda}{n}
\end{align}
$$
上記が$[2]$で計算した$J_{n}(\lambda)$の逆数$J_{n}(\lambda)^{-1}$に一致することから、クラメル・ラオの不等式の下限と一致すると考えることができる。これにより、標本平均が有効推定量に一致すると考えられる。
$[4]$
標本平均$\bar{X}$に関して中心極限定理を考えることにより、$\sqrt{n}(\bar{X}-\lambda)$は正規分布$N(0,\lambda)$に分布収束することがわかる。これにより最尤推定量の漸近正規性を示すことができる。
また、この場合の漸近分散の$\lambda$がフィッシャー情報量の逆数の$J_{1}(\lambda)^{-1}=\lambda$と一致することから漸近有効性も成立していると考えることができる。
問8.3
$[1]$
推定量$T_1, T_2$の期待値$E[T_1], E[T_2]$はそれぞれ下記のように考えられる。
$$
\large
\begin{align}
E[T_1] &= E[\bar{X}^2] \\
&= E[\bar{X}]^2 + V[\bar{X}] \\
&= \mu^2 + \frac{\sigma^2}{n} \\
E[T_2] &= E \left[ \frac{1}{n} \sum_{i=1}^{n} X_i^2 \right] \\
&= \frac{1}{n} E \left[ \sum_{i=1}^{n} X_i^2 \right] \\
&= \frac{n}{n} E[X_i^2] \\
&= E[X_i]^2 + V[X_i] \\
&= \mu^2 + \sigma^2
\end{align}
$$
よって、$T_1,T_2$のバイアス$b_1(\mu,\sigma^2), b_2(\mu,\sigma^2)$はそれぞれ下記のように得られる。
$$
\large
\begin{align}
b_1(\mu,\sigma^2) &= E[T_1] – \mu^2 \\
&= \mu^2 + \frac{\sigma^2}{n} – \mu^2 \\
&= \frac{\sigma^2}{n} \\
b_2(\mu,\sigma^2) &= E[T_2] – \mu^2 \\
&= \mu^2 + \sigma^2 – \mu^2 \\
&= \sigma^2
\end{align}
$$
$[2]$
半径の計測値から各面積を計算しその平均値を推定に用いる場合、コインの面積$\pi r^2$の推定量に$\pi T_2$を用いることに一致する。$[1]$より推定量$T_2$のバイアスは$\sigma^2$であり、$n$を増やしてもこのバイアスは減らない。
一方で$T_1$のバイアスは$\displaystyle \frac{\sigma^2}{n}$であり、$n \to \infty$で$0$に収束する。このように推定量の選定にあたってはサンプル数の$n$が増大するに連れてバイアスが小さくなる推定量を選定しなければならないので、$T_2$の推定量を用いる当該手法には問題がある。
$[3]$
下記のように計算を行うことができる。
import numpy as np
x = np.array([8.4, 9.0, 8.2, 10.4, 9.2])
mean_x = np.mean(x)
s2 = np.sum((x-mean_x)**2)/(x.shape[0]-1)
modified_T1 = mean_x**2 - s2/x.shape[0]
estimate = np.pi*modified_T1
print("mean_x: {:.1f}".format(mean_x))
print("unbiased variance: {:.1f}".format(s2))
print("estimated value: {:.1f}".format(estimate))・実行結果
> print("mean_x: {:.1f}".format(mean_x))
mean_x: 9.0
> print("unbiased variance: {:.1f}".format(s2))
unbiased variance: 0.7
> print("estimated value: {:.1f}".format(estimate))
estimated value: 256.3$[4]$
下記を実行することで計算できる。
import numpy as np
x = np.array([8.4, 9.0, 8.2, 10.4, 9.2])
mean_x = np.mean(x)
x_sub = np.zeros(5)
for i in range(x.shape[0]):
a = 0
for j in range(x.shape[0]):
if i != j:
a += x[j]
x_sub[i] = (a/(x.shape[0]-1))**2
x_sub_mean = np.mean(x_sub)
bias = (x.shape[0]-1)*(x_sub_mean - mean_x**2)
est_jack = mean_x**2 - bias
estimated_value = np.pi*est_jack
print("modified estimated value: {:.1f}".format(estimated_value))・実行結果
> print("modified estimated value: {:.1f}".format(estimated_value))
modified estimated value: 256.3$[5]$
$\bar{X}$に関する中心極限定理により、$\sqrt{n}(\bar{X}-\mu)$は$\mathcal{N}(0,\sigma^2)$に分布収束する。ここで$f(x)=x^2$に対してデルタ法を適用することを考える。
このとき$\sqrt{n}(f(\bar{X})-f(\mu))$は$\mathcal{N}(0,\sigma^2(f'(\mu))^2) = \mathcal{N}(0,\sigma^2(2 \mu)^2) = \mathcal{N}(0,4\mu^2\sigma^2)$に分布収束すると考えられ、同時に漸近正規性が成立することが確かめられる。
・考察
ここで行なった結果が妥当かどうか確認するにあたって、下記で正規分布からの標本を元にPythonを用いて結果の検証を行なった。
https://www.hello-statisticians.com/explain-terms-cat/bias1.html
参考
・準$1$級関連まとめ
https://www.hello-statisticians.com/toukeikentei-semi1

[…] 「統計学実践ワークブック」の$8$章「統計的推定の基礎」のバイアスやジャックナイフ推定量に関する直感的な理解が難しいように思われたので、当記事では具体的に正規分布から標本を発生させることでいくつかの値の確認を行いました。ワークブック問$8.3$を主に参考に作成を行いました。 […]