ブログ

強化学習(Reinforcement Learning)は数式が多く一見難しそうに見えますが、統計学の確率分布の表記に慣れていれば実はそれほど難しくありません。そこで何回かにわけて強化学習の基本トピックに関して取り扱いを行います。
第$1$回は強化学習の問題設定を理解するにあたって「有限マルコフ決定過程(Finite Markov Decision Process)」を取り扱います。Richard S. Suttonの”Reinforcement Learning, second edition: An Introduction“のChapter$3$を参考に作成を行いました。

Reinforcement Learning, second edition: An Introduction (Adaptive Computation and Machine Learning s…

Sutton, Richard S., Barto, Andrew G.

16,437円(11/09 09:54時点)

Amazon

基本的な理論の確認

MDPの概要

有限マルコフ決定過程(Finite Markov Decision Process)は逐次的意思決定(sequential decision making)のよく用いられてきた定式化である。

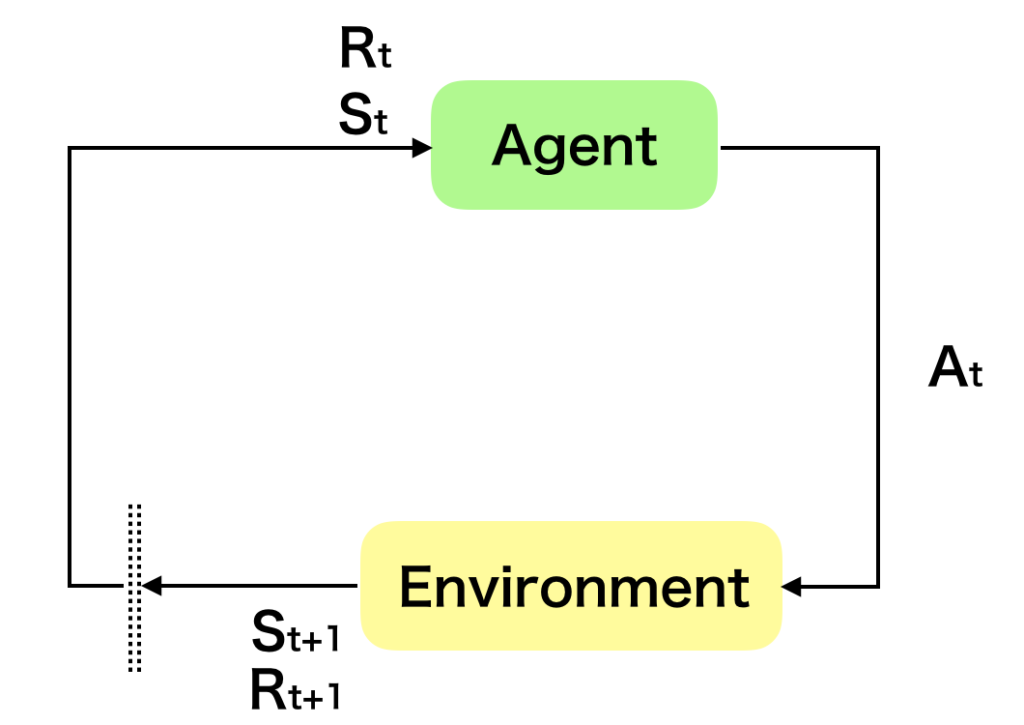
強化学習の図式化では上のような図がよく用いられるが、これは逐次的意思決定問題の$1$ステップを切り抜いたものであると理解すると良い。エージェント(Agent)が環境(Environment)から状態$S_t$と報酬$R_t$を観測し、行動$A_t$を行うことで次の状態$S_{t+1}$と次の報酬$R_{t+1}$を観測するというのが一連の流れである。ここで$S_{t}$に対して$A_{t}$を実行した際の報酬を$R_t$と定義するか$R_{t+1}$と定義するかは議論の余地があるように思われるが、参照した”Reinforcement Learning, second edition: An Introduction”では$R_{t+1}$を用いているので以下では$R_{t+1}$を用いる。

このように状態$S_t$、報酬$R_t$、行動$A_t$を定義し、実際に一連のプロセスを実行すると下記のような系列(trajectory)が得られる。
$$
\large
\begin{align}
S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, …
\end{align}
$$

上記のように考える場合、行列形式で系列を保存することが難しいならば、$R_0=0$とおいて$R_0, S_0, A_0, …$とすることもできると考えられる。また、$S_t, A_t, R_t$はそれぞれ集合表記を用いて下記のように表すことができることも抑えておくと良い。
$$
\large
\begin{align}
S_{t} & \in \mathcal{S} \\
A_{t} & \in \mathcal{A} \\
R_{t} & \in \mathcal{R} \subset \mathbb{R}
\end{align}
$$

状態遷移確率と方策

強化学習を考える上で数式が難しくなりがちなのが状態遷移確率(state-transition probabilities)と方策(policy)である。どちらもエージェントの行動に基づいて状態が遷移する際に用いられる確率分布であるが、「方策」が状態に対するエージェントの行動の確率分布である一方で、「状態遷移確率」はエージェントの行動を受けて環境が状態を変化させるときの確率分布であることは抑えておく必要がある。

方策$\pi(a|s)$は確率分布を表す$P$を用いて下記のように表すことができる。
$$
\large
\begin{align}
\pi(a|s) = P(A_t=a|S_t=s)
\end{align}
$$

また、状態遷移確率$p(s’,r|s,a)$は同様に$P$を用いて下記のように表すことができる。
$$
\large
\begin{align}
p(s’,r|s,a) = P(S_{t+1}=s’,R_{t+1}=r|S_t=s,A_{t}=a)
\end{align}
$$

状態遷移確率$p(s’,r|s,a)$と方策$\pi(a|s)$は価値関数を定義する際にどちらも出てくるのでそれぞれ抑えておく必要がある。方策はエージェント、状態遷移確率は環境が持つ確率分布であると把握しておくとわかりやすいと思われる。

エピソードと報酬和(return)

強化学習の目的は一連の逐次的意思決定$S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, …$が完了するまでの獲得報酬を最大化することにある。この一連の意思決定$1$回の単位はエピソード(episode)とされることが多い。

$1$エピソードにおける$t$以降の報酬の和$G_{t}$を下記のように定義することを考える。
$$
\large
\begin{align}
G_{t} & \equiv R_{t+1} + \gamma R_{t+2} + … \\
&= \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \quad (1)
\end{align}
$$

上記の$\gamma$は$0 \leq \gamma \leq 1$を定義域に取り、割引率(discount rate)と呼ばれる。割引率は即時(immediate)に得られる報酬を将来的に得られる報酬よりも重視するという考え方である。

また、$G_{t}$に関して下記のような変形を行うことができる。
$$
\large
\begin{align}
G_{t} & \equiv R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + … \\
&= R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + … ) \\
&= R_{t+1} + \gamma (R_{(t+1)+1} + \gamma R_{(t+1)+2} + … ) \\
&= R_{t+1} + \gamma \sum_{k=0}^{\infty} \gamma^{k} R_{(t+1)+k} \\
&= R_{t+1} + \gamma G_{t+1} \quad (2)
\end{align}
$$

上記で表した$(2)$は数列における漸化式と同様に理解すると良い。$(1)$式、$(2)$式はそれぞれ、数列${ a_{n} }$の$a_{n}$和を$S_{n}$のようにおいた際の下記の式にそれぞれ対応する。
$$
\large
\begin{align}
S_{n} &= \sum_{n}^{\infty} a_x \quad (1)’ \\
S_{n} &= \sum_{n}^{\infty} a_x = a_{n} + a_{n+1} + … \\
&= a_{n} + (a_{n+1} + a_{n}+2 + …) = a_{n} + \sum_{n+1}^{\infty} a_x \quad (2)’
\end{align}
$$

価値関数(value function)・ベルマン方程式(Bellman equation)

強化学習のほぼ全てのアルゴリズムは価値関数(value function)の推定に関係する。

価値関数は状態の価値(how good)を評価する関数だが、状態の価値は以後の報酬和の期待値(expected return)の点から定義される。

方策$\pi(a|s)$に対応する状態$s$の状態価値関数(state-value function)を$v_{\pi}(s)$とおくと、$v_{\pi}(s)$は下記のように定義される。
$$
\large
\begin{align}
v_{\pi}(s) & \equiv \mathbb{E}_{\pi} [G_{t}|S_{t}(s)] \\
&= \mathbb{E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \Bigr| S_{t}=(s) \right], \quad s^{\forall} \in \mathcal{S} \quad (3)
\end{align}
$$

また、状態$s$の価値と同様に状態$s$における行動$a$の価値を計算できると良い場合も多い。よって、状態$s$における行動$a$の価値を表す行動価値関数(action-value function)を$q_{\pi}(s,a)$とおき、下記のように定義される。
$$
\large
\begin{align}
q_{\pi}(s,a) & \equiv \mathbb{E}_{\pi} [G_{t}|S_{t}(s)] \\
&= \mathbb{E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \Bigr| S_{t}=(s),A_{t}=(a) \right]
\end{align}
$$

$(3)$式は前項で取り扱った報酬和に関する変形に基づいて下記のように変形を行うことができる。
$$
\large
\begin{align}
v_{\pi}(s) &= \mathbb{E}_{\pi} [G_{t}|S_{t}(s)] \\
&= \mathbb{E}_{\pi} [R_{t+1} + \gamma G_{t+1}|S_{t}(s)] \\
&= \sum_{a} \pi(a|s) \sum_{s’,r} p(s’,r|s,a) \left[ r + \gamma v_{\pi}(s’) \right], \quad s^{\forall} \in \mathcal{S}
\end{align}
$$

上記を$v_{\pi}$に関するベルマン方程式(Bellman equation)という。

最適方策・最適状態価値関数

強化学習の目的は推定した価値関数などを元に報酬を最大化する方策を見つけることにある。これを最適方策(optimal policy)と定義する。

ここで方策$\pi_{*}$が最適方策であるということは、全ての状態$s$に対して下記が成立することに対応する。
$$
\large
\begin{align}
v_{\pi_{*}}(s) \geq v_{\pi}(s), \quad s^{\forall} \in \mathcal{S}
\end{align}
$$

最適方策に対応する状態価値関数を最適状態価値関数(optimal state-value function)という。ここで、最適状態価値関数を$v_{*}$と定めるとき、$v_{*}(s)$は下記のように表すことができる。
$$
\large
\begin{align}
v_{*}(s) = v_{\pi_{*}}(s) = \max_{\pi} v_{\pi}(s)
\end{align}
$$

上記の数式の解釈にあたっては$\displaystyle \max_{\pi} v_{\pi}(s)$が$v_{\pi}(s)$を最大化する$\pi$に基づく$v_{\pi}(s)$の値を表すことは抑えておくと良い。

また、最適方策に対応する行動価値関数を最適行動価値関数(optimal action-value function)という。ここで、最適行動価値関数を$q_{*}$と定めるとき、$q_{*}(s,a)$は下記のように表すことができる。
$$
\large
\begin{align}
q_{*}(s,a) = q_{\pi_{*}}(s,a) = \max_{\pi} q_{\pi}(s,a)
\end{align}
$$

具体例の確認

ワイブル分布(Weibul distribution)は瞬間故障率の変化を表す際によく用いられる分布であり、瞬間故障率が一定である指数分布の拡張であると考えることもできる。当記事ではワイブル分布の定義や、期待値・分散・瞬間故障率などの導出に関して取り扱った。
「基礎統計学Ⅰ 統計学入門(東京大学出版会)」の$6.13$節の「ワイブル分布」や「統計学実践ワークブック」の$19$章の「回帰分析その他」を参考に作成を行なった。

統計学入門 (基礎統計学Ⅰ)

3,080円(11/09 03:56時点)

Amazon

日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック

3,080円(11/09 13:11時点)

Amazon

ワイブル分布の定義とその理解

ワイブル分布の定義

パラメータ$\lambda, p$のワイブル分布(Weibul distribution)の確率密度関数を$f(t)$とおくと、定義域$t \geq 0$における$f(t)$は下記のように表される。
$$
\large
\begin{align}
f(t) = \lambda p (\lambda t)^{p-1} e^{-(\lambda t)^p}, \quad t \geq 0
\end{align}
$$

上記は「統計学実践ワークブック」の$19$章の定義であるが、「基礎統計学Ⅰ 統計学入門(東京大学出版会)」では$\displaystyle a = \frac{1}{\lambda}, b=p$と置き換えることで下記のように定義される。
$$
\large
\begin{align}
f(t) &= \lambda p (\lambda t)^{p-1} e^{-(\lambda t)^p} \\
&= \frac{b}{a} \times \frac{t^{p-1}}{a^{p-1}} \exp \left( -\frac{t^{b}}{a^{b}} \right) \\
&= \frac{b t^{p-1}}{a^{p}} \exp \left[ – \left( \frac{t^{b}}{a^{b}} \right)^{p} \right], \quad t \geq 0
\end{align}
$$

ワイブル分布と指数分布

ワイブル分布は指数分布の拡張であるので、逆に指数分布はワイブル分布の一例に相当する。このことは前項で確認した確率密度関数$f(t)$に対し、$p=1$を代入することで確認できる。
$$
\large
\begin{align}
f(t) &= \lambda p (\lambda t)^{p-1} e^{-(\lambda t)^p} \\
&= \lambda \times 1 \times (\lambda t)^{1-1} e^{-(\lambda t)^1} \\
&= \lambda e^{-\lambda t}
\end{align}
$$

上記が指数分布の確率密度関数の式に一致する。よって、指数分布はワイブル分布を考えた際に$p=1$となる確率分布であるということが確認できる。

微分方程式を用いた指数分布・ワイブル分布の確率密度関数の導出

累積分布関数$F(t)$や確率密度関数$f(t)$はハザード関数$h(t)$に関する下記の微分方程式を$F(0)=0$の条件下で解くことで導出することができる。
$$
\large
\begin{align}
\frac{d}{dx} (\log{(1-F(x))}) = -h(x)
\end{align}
$$

上記の詳しい導出は「統計学ワークブック19章のまとめ」の「ハザード関数と微分方程式」で取り扱った。

指数分布の方が取り扱いやすいので以下、「指数分布」、「ワイブル分布」の順に導出の確認を行う。

・指数分布
指数分布におけるハザード関数は$h(t)=\lambda$のように表される。このとき微分方程式$\displaystyle \frac{d}{dx} (\log{(1-F(x))}) = -h(x)$は下記のように変形できる。
$$
\large
\begin{align}
\frac{d}{dx} (\log{(1-F(x))}) &= -h(x) \\
\log{(1-F(x))} &= – \int h(x) dx \\
\log{(1-F(x))} &= – \int \lambda dx \\
\log{(1-F(x))} &= – \lambda x + C
\end{align}
$$

上記に対し$x=0, F(0)=0$を代入すると積分定数$C$に関して下記が得られる。
$$
\large
\begin{align}
\log{(1-F(x))} &= – \lambda x + C \\
\log{(1-0)} &= – \lambda \times 0 + C \\
C &= 0
\end{align}
$$

よって、$\log{(1-F(x))} = – \lambda x$のように表すことができ、この式に基づいて$F(x)$と$f(x)$は下記のように導出できる。
$$
\large
\begin{align}
\log{(1-F(x))} &= – \lambda x \\
1 – F(x) &= e^{-\lambda x} \\
F(x) &= 1 – e^{-\lambda x} \\
f(x) &= \frac{d}{dx} F(x) \\
&= \lambda e^{-\lambda x}
\end{align}
$$

上記は指数分布の累積分布関数と確率密度関数の式に一致する。

・ワイブル分布
ワイブル分布におけるハザード関数は$h(t)=\lambda p (\lambda t)^{p-1}$のように表される。このとき微分方程式$\displaystyle \frac{d}{dx} (\log{(1-F(x))}) = -h(x)$は下記のように変形できる。
$$
\large
\begin{align}
\frac{d}{dx} (\log{(1-F(x))}) &= -h(x) \\
\log{(1-F(x))} &= – \int h(x) dx \\
\log{(1-F(x))} &= – \int \lambda p (\lambda x)^{p-1} dx \\
\log{(1-F(x))} &= – \frac{1}{p} \lambda^{p} p x^{p} + C \\
&= -(\lambda x)^{p} + C
\end{align}
$$

上記に対し$x=0, F(0)=0$を代入すると積分定数$C$に関して下記が得られる。
$$
\large
\begin{align}
\log{(1-F(x))} &= -(\lambda x)^{p}+ C \\
\log{(1-0)} &= – 0 + C \\
C &= 0
\end{align}
$$

よって、$\log{(1-F(x))} = -(\lambda x)^{p}$のように表すことができ、この式に基づいて$F(x)$と$f(x)$は下記のように導出できる。
$$
\large
\begin{align}
\log{(1-F(x))} &= -(\lambda x)^{p} \\
1 – F(x) &= e^{-(\lambda x)^{p}} \\
F(x) &= 1 – e^{-(\lambda x)^{p}} \\
f(x) &= \frac{d}{dx} F(x) \\
&= – e^{-(\lambda x)^{p}} \times (-p(\lambda x)^{p-1}) \times \lambda \\
&= \lambda p (\lambda x)^{p-1} e^{-(\lambda x)^{p}}
\end{align}
$$

上記はワイブル分布の累積分布関数と確率密度関数の式に一致する。

・参考

日本統計学会公式認定 統計検定1級対応 統計学

3,520円(11/09 17:03時点)

Amazon

ワイブル分布の期待値・分散・瞬間故障率の計算

ワイブル分布の期待値$E[X]$の計算

ワイブル分布の期待値$E[X]$は確率密度関数$f(x)$を用いて下記のように表すことができる。
$$
\large
\begin{align}
E[X] &= \int_{0}^{\infty} x \times f(x) dx \\
&= \int_{0}^{\infty} x \times \lambda p (\lambda x)^{p-1} e^{-(\lambda x)^p} dx \\
&= \int_{0}^{\infty} p (\lambda x)^{p} e^{-(\lambda x)^p} dx \quad (1)
\end{align}
$$

上記の積分に対し、$u = (\lambda x)^{p}$を定め変数変換を行うことを考える。$u = (\lambda x)^{p}$を$x$について解き$u$で微分を行うと下記がそれぞれ得られる。
$$
\large
\begin{align}
(\lambda x)^{p} &= u \\
\lambda x &= u^{\frac{1}{p}} \\
x &= \frac{u^{\frac{1}{p}}}{\lambda} \quad (2) \\
\frac{dx}{du} &= \frac{d}{du} \left( \frac{u^{\frac{1}{p}}}{\lambda} \right) \\
&= \frac{u^{\frac{1}{p}-1}}{p \lambda} \quad (3)
\end{align}
$$

$(2)$式、$(3)$式を元に$(1)$式は下記のように変数変換できる。
$$
\large
\begin{align}
E[X] &= \int_{0}^{\infty} p (\lambda x)^{p} e^{-(\lambda x)^p} dx \\
&= \int_{0}^{\infty} p u e^{-u} \times \frac{u^{\frac{1}{p}-1}}{p \lambda} du \\
&= \frac{1}{\lambda} \int_{0}^{\infty} u^{1+\frac{1}{p}-1} e^{-u} du = \frac{1}{\lambda} \Gamma \left( 1+\frac{1}{p} \right) \quad (4)
\end{align}
$$

上記の変形にあたっては下記のガンマ関数$\Gamma(a)$の定義を用いた。
$$
\large
\begin{align}
\Gamma(a) = \int_{0}^{\infty} x^{a-1} e^{-x} dx
\end{align}
$$

・参考
ガンマ分布
https://www.hello-statisticians.com/explain-terms-cat/gamma_distribution1.html
変数変換
https://www.hello-statisticians.com/practice/stat_practice15.html

ワイブル分布の分散$V[X]$の計算

分散$V[X]$の計算にあたっては$V[X]=E[X^2]-E[X]^2$を元に考えることで前項の$(4)$式の結果を活用することができる。以下、$E[X^2]$の導出の確認を行う。
$$
\large
\begin{align}
E[X^2] &= \int_{0}^{\infty} x^2 \times f(x) dx \\
&= \int_{0}^{\infty} x^2 \times \lambda p (\lambda x)^{p-1} e^{-(\lambda x)^p} dx \\
&= \int_{0}^{\infty} p (\lambda x)^{p} x e^{-(\lambda x)^p} dx \quad (5)
\end{align}
$$

上記の積分に対し、前項と同様に$u = (\lambda x)^{p}$を定め変数変換を行うことを考える。前項で導出を行なった$(2)$式、$(3)$式を元に$(5)$式は下記のように変数変換できる。
$$
\large
\begin{align}
E[X] &= \int_{0}^{\infty} p (\lambda x)^{p} x e^{-(\lambda x)^p} dx \\
&= \int_{0}^{\infty} p u \frac{u^{\frac{1}{p}}}{\lambda} e^{-u} \times \frac{u^{\frac{1}{p}-1}}{p \lambda} du \\
&= \frac{1}{\lambda^2} \int_{0}^{\infty} u^{1+\frac{2}{p}-1} e^{-u} du = \frac{1}{\lambda^2} \Gamma \left( 1+\frac{2}{p} \right)
\end{align}
$$

$(4)$式、$(6)$式に基づいて$V[X]$は下記のように表すことができる。
$$
\large
\begin{align}
V[X] &= E[X^2] – E[X]^2 \\
&= \frac{1}{\lambda^2} \Gamma \left( 1+\frac{2}{p} \right) – \left( \frac{1}{\lambda} \Gamma \left( 1+\frac{1}{p} \right) \right)^2 \\
&= \frac{1}{\lambda^2} \left[ \Gamma \left( 1+\frac{2}{p} \right) – \Gamma \left( 1+\frac{1}{p} \right)^2 \right]
\end{align}
$$

・参考
期待値、分散の公式
https://www.hello-statisticians.com/explain-terms-cat/expectation-variance-covariance.html
ガンマ分布
https://www.hello-statisticians.com/explain-terms-cat/gamma_distribution1.html
変数変換
https://www.hello-statisticians.com/practice/stat_practice15.html

ワイブル分布の瞬間故障率$h(t)$の計算

$$
\large
\begin{align}
f(t) = \lambda p (\lambda t)^{p-1} e^{-(\lambda t)^p}, \quad t \geq 0
\end{align}
$$
上記で表したワイブル分布の確率密度関数$f(t)$を元に、累積分布関数$F(t)$、生存関数$S(t)$、ハザード関数$h(t)$を導出する。なお、ハザード関数は瞬間故障率と呼ばれることもある。

・累積分布関数$F(t)$
$$
\large
\begin{align}
F(t) &= \int_{0}^{t} f(x) dx \\
&= \int_{0}^{t} \lambda p (\lambda x)^{p-1} e^{-(\lambda x)^p} dx \\
&= \int_{0}^{t} \frac{d}{dx} \left( – e^{-(\lambda x)^p} \right) dx \\
&= \left[ – e^{-(\lambda x)^p} \right]_{0}^{t} \\
&= 1 – e^{-(\lambda t)^p}
\end{align}
$$

・生存関数$S(t)$
$$
\large
\begin{align}
S(t) &= 1 – F(t) \\
&= 1 – (1 – e^{-(\lambda t)^p}) \\
&= e^{-(\lambda t)^p}
\end{align}
$$

・ハザード関数、瞬間故障率$h(t)$
$$
\large
\begin{align}
h(t) &= \frac{f(t)}{S(t)} \\
&= \frac{\lambda p (\lambda t)^{p-1} e^{-(\lambda t)^p}}{e^{-(\lambda t)^p}} \\
&= \lambda p (\lambda t)^{p-1}
\end{align}
$$

ハザード関数$h(t)$の解釈にあたっては、まず$p=1$のとき$h(t)=\lambda$となり、指数関数のハザード関数と一致することは抑えておくと良い。また、ハザード関数が$t$の増加に伴い増大するか減少するかを確認することで機械の劣化による故障率の増加を表すことができる。

ここで$h(t) = \lambda p (\lambda t)^{p-1}$の関数は、$p>1$であれば$t$の増加に伴い$h(t)$が増大し、$p<1$であれば$t$の増加に伴い$h(t)$が減少することが関数を確認することでわかる。

「$t$の増加に伴い$h(t)$が増大すること」をIFR(Increasing Failure Rate)、「$t$の増加に伴い$h(t)$が減少すること」をDFR(Decreasing Failure Rate)ということも合わせて抑えておくと良い。

参考

・統計学実践ワークブック19章： 回帰分析その他
・赤本 章末課題6.6： 指数分布の瞬間故障率
・統計検定 1級 理工学 出題問題

乱数を用いたモンテカルロ法はモンテカルロ積分やMCMCなど、様々な応用に用いられます。モンテカルロ積分の計算手順自体はそれほど難しくない一方で、数式上は難しそうな表記がなされることが多いので当記事では直感的な理解ができるように取り扱いを行いました。
作成にあたっては「統計学実践ワークブック」の数式表記やWikipediaの定義などを参考に取りまとめを行いました。

日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック

3,080円(11/09 13:11時点)

Amazon

モンテカルロ積分の概要

モンテカルロ法とモンテカルロ積分

「統計学実践ワークブック」ではモンテカルロ法とモンテカルロ積分の使い分けがわかりにくいので、Wikipediaの内容の参照を行う。

In mathematics, Monte Carlo integration is a technique for numerical integration using random numbers. It is a particular Monte Carlo method that numerically computes a definite integral.

https://en.wikipedia.org/wiki/Monte_Carlo_integration

モンテカルロ積分(Monte Carlo integration)はモンテカルロ法(a particular Monte Carlo method)の一種とあり、「モンテカルロ法に内包される手法である」と考えると良い。

「モンテカルロ法」は「乱数を用いた計算」を指すので、「モンテカルロ積分」は「乱数を用いた積分値の計算」に対応すると理解しておくと良いと思われる。具体的な積分の式表示に関しては次項で取りまとめを行う。

$0 \leq x \leq 1$区間のモンテカルロ積分

$$
\large
\begin{align}
\theta = \int_{0}^{1} g(x) dx
\end{align}
$$

モンテカルロ積分は一様乱数を用いて上記の$\theta$の推定を行う手法である。ここでの積分の区間が$0 \leq x \leq 1$であることから、一様分布$U[0,1]$に基づいて乱数を生成し、これを用いて$\theta$を推定することを考える。

確率変数$X$が$X \sim U[0,1]$であるとき、$g(X)$の期待値$E[g(X)]$に関して下記が成立する。
$$
\large
\begin{align}
E[g(X)] &= \int_{0}^{1} g(x) f(x) dx \\
&= \int_{0}^{1} g(x) \times 1 dx = \int_{0}^{1} g(x) dx
\end{align}
$$

上記で用いた$f(x)$は一様分布$U[0,1]$の確率密度関数であるので、$0 \leq x \leq 1$の区間では$f(x)=1$であることを元に代入を行なった。ここで下記のように$g(X_1),…,g(X_m)$の標本平均$\hat{\theta}$を考える。
$$
\large
\begin{align}
\hat{\theta} = \frac{1}{m} \sum_{i=1}^{m} g(X_i)
\end{align}
$$

ここで$m \to \infty$のとき、大数の弱法則より$\displaystyle \frac{1}{m} \sum_{i=1}^{m} g(X_i) \to E[g(X)]$が成立する。これは$\displaystyle \lim_{m \to \infty} \hat{\theta} = \theta$と同義である。

ここまでは原理の確認を行なったが、実際にモンテカルロ積分を行う際は$U[0,1]$にしたがって$x_1,…,x_n$のサンプリングを行なったのちに、$g(x_1),…,g(x_n)$の標本平均を計算することで$\theta$の推定を行うと考えておくとよい。

下記にPythonを用いた$\displaystyle \theta = \int_{0}^{1} e^x dx$の推定の例を示す。

import numpy as np

np.random.seed(20)

x_100 = np.random.rand(100)
x_1000 = np.random.rand(1000)
x_10000 = np.random.rand(10000)
x_100000 = np.random.rand(100000)
y_100 = np.e**x_100
y_1000 = np.e**x_1000
y_10000 = np.e**x_10000
y_100000 = np.e**x_100000


print("Population theta: {:.5f}".format(np.e-1))
print("n=100, Estimated theta: {:.5f}".format(np.mean(y_100)))
print("n=1000, Estimated theta: {:.5f}".format(np.mean(y_1000)))
print("n=10000, Estimated theta: {:.5f}".format(np.mean(y_10000)))
print("n=100000, Estimated theta: {:.5f}".format(np.mean(y_100000)))

・実行結果

Population theta: 1.71828
n=100, Estimated theta: 1.73545
n=1000, Estimated theta: 1.70142
n=10000, Estimated theta: 1.73034
n=100000, Estimated theta: 1.71785

実行結果より$n=100,000$の精度が一番高いことが確認できる。また、$n=10000$の精度はあまり良くないが、乱数の設定によっては十分生じうると考えておくと良いと思われる。

区間が$0 \leq x \leq 1$でない場合のモンテカルロ積分

前項では$0 \leq x \leq 1$区間におけるモンテカルロ積分に関して確認を行なったが、当項では区間を変えた際のモンテカルロ積分をどのように計算するかについて確認を行う。

$$
\large
\begin{align}
\theta = \int_{0}^{3} e^{x} dx
\end{align}
$$
以下、具体的に上記のように$g(x)=e^{x}$の$0 \leq x \leq 3$の区間での積分値の推定に関して考える。

$$
\large
\begin{align}
\int_{0}^{3} e^{x} dx = \int_{0}^{1} e^{x} dx + \int_{1}^{2} e^{x} dx + \int_{2}^{3} e^{x} dx
\end{align}
$$
積分値の推定にあたっては上記のように積分の式を分解して考えることで、モンテカルロ積分を行う際に用いる確率密度関数を該当区間で$f(x)=1$となる一様分布に設定することができ、そのまま推定値を計算するだけで良いのでシンプルに考えることができる。

前項のPythonの処理に基づいて$\displaystyle \theta = \int_{0}^{3} e^x dx$の推定の例を示す。

import numpy as np

np.random.seed(20)

theta = 0
for i in range(3):
    x = np.random.rand(100000) + i
    y = np.e**x
    theta += np.mean(y)


print("Population theta: {:.5f}".format(np.e**3-1))
print("Estimated theta: {:.5f}".format(theta))

・実行結果

Population theta: 19.08554
Estimated theta: 19.09739

モンテカルロ積分の精度

推定値の分散・標準偏差の計算

$$
\large
\begin{align}
\hat{\theta} = \frac{1}{m} \sum_{i=1}^{m} g(X_i)
\end{align}
$$

モンテカルロ積分は上記の式を元にパラメータ$\hat{\theta}$の推定値を計算する手法である。これは$\theta$は$\displaystyle \lim_{m \to \infty} \hat{\theta} = \theta = E[g(X_i)] = E[g(X)]$のように考えることができることに基づくが、ここで推定量・推定値に対応する$\hat{\theta}$に対して、$\hat{\theta}$の分散$V[\hat{\theta}]$や標準偏差$SD[\hat{\theta}]$は推定値の精度に対応すると考えることができることは抑えておくと良い。

以下$g(x) = e^x$に対して$X_1,…,X_m \sim U[0,1]$を用いて$\displaystyle \theta = \int_{0}^{1} e^x dx$を推定する際の標準偏差に関して考える。先に$g(X)$の分散$V[g(X)]$の計算を行う。
$$
\large
\begin{align}
V[g(X)] &= E[(g(X)-E[g(x)])^2] \\
&= \int_{0}^{1} \left( g(x) – \int_{0}^{1} g(x) dx \right)^2 dx \\
&= \int_{0}^{1} \left( e^x – \int_{0}^{1} e^x dx \right)^2 dx \\
&= \int_{0}^{1} \left( e^x – \left[ e^x \right]_{0}^{1} \right)^2 dx \\
&= \int_{0}^{1} ( e^x – e + 1 )^2 dx \\
&= \sigma_g^2
\end{align}
$$
上記では結果を$\sigma_g^2$のようにおいたが、推定値の標準偏差を考える場合は実際には値が与えられる場合や推定を行なった値を用いると考えておくとよい。

次に$X_1,…,X_n$が$i.i.d.$のとき、分散$V[\hat{\theta}]$を上記の$\sigma_g^2$を用いて表すことを考える。
$$
\large
\begin{align}
V[\hat{\theta}] &= V \left[ \frac{1}{m} \sum_{i=1}^{m} g(X_i) \right] \\
&= \frac{1}{m^2} V \left[ \sum_{i=1}^{m} g(X_i) \right] \\
&= \frac{1}{m^2} \times m \times V[g(X_i)] \\
&= \frac{1}{m} V[g(X_i)] \\
&= \frac{\sigma_g^2}{m}
\end{align}
$$

上記より、推定量・推定値の標準偏差$SD[\hat{\theta}]$は下記のように表すことができる。
$$
\large
\begin{align}
SD[\hat{\theta}] &= \sqrt{V[\hat{\theta}]} \\
&= \frac{\sigma_g}{\sqrt{m}}
\end{align}
$$

・参考
期待値、分散の公式

精度の向上

参考

・自然科学の統計学 解答
・統計学実践ワークブック 解答