Pythonを用いたMCMCのプログラミング〜メトロポリス法、HMC法、NUTS etc〜

数式だけの解説ではわかりにくい場合もあると思われるので、統計学の手法や関連する概念をPythonのプログラミングで表現します。当記事ではMCMCを取扱う際に出てくるメトロポリスヘイスティングス法、HMC法、NUTSなどの手法に関して取り扱います。

・Pythonを用いた統計学のプログラミングまとめ
https://www.hello-statisticians.com/stat_program

Contents

1 基本的な手法
2 発展的な手法

基本的な手法

メトロポリス法

$$
\large
\begin{align}
f(x) &= 0.1 \phi(-2) + 0.7 \phi(0) + 0.1 \phi(5) \\
\phi(\mu) &= \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{(x-\mu)^2}{2} \right)
\end{align}
$$
上記の数式に基づく混合分布を目標分布と考えるとき、下記を実行することで混合分布の描画を行うことができる。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

x = np.arange(-10.,10.01,0.01)
f_x = 0.2*stats.norm.pdf(x,-2.,1.) + 0.7*stats.norm.pdf(x,0.,1.) + 0.2*stats.norm.pdf(x,5.,1.)

plt.plot(x,0.1*stats.norm.pdf(x,-2.,1.),"b--")
plt.plot(x,0.7*stats.norm.pdf(x,0.,1.),"b--")
plt.plot(x,0.2*stats.norm.pdf(x,5.,1.),"b--")
plt.plot(x,f_x,color="green")
plt.show()

・実行結果

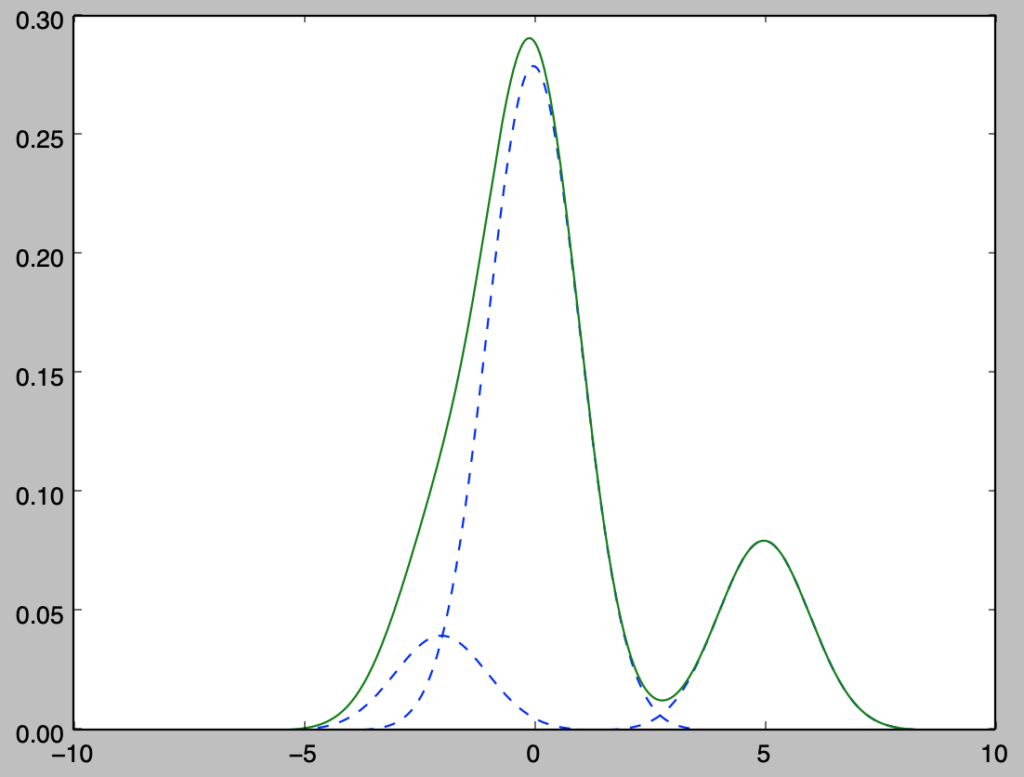
以下、ここまでで定義を行なった$f(x)$をメトロポリス法によるサンプリングを元に再現することを考える。下記を実行することでメトロポリス法に基づいてサンプリングや結果の描画を行うことができる。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

np.random.seed(0)

def f(x):
    return 0.2*stats.norm.pdf(x,-2.,1.) + 0.7*stats.norm.pdf(x,0.,1.) + 0.2*stats.norm.pdf(x,5.,1.)

x = np.arange(-10.,10.01,0.01)
f_x = f(x)

burn_in = 1000
res = np.zeros(10000)
y = 0.
for i in range(burn_in+res.shape[0]):
    y_candidate = y + 0.5*stats.norm.rvs()
    r = f(y_candidate) / f(y)
    u = np.random.rand()
    if u < r:
        y = y_candidate
        if i > burn_in:
            res[i-burn_in] = y

plt.hist(res,bins=20,color="limegreen")
plt.show()

・実行結果

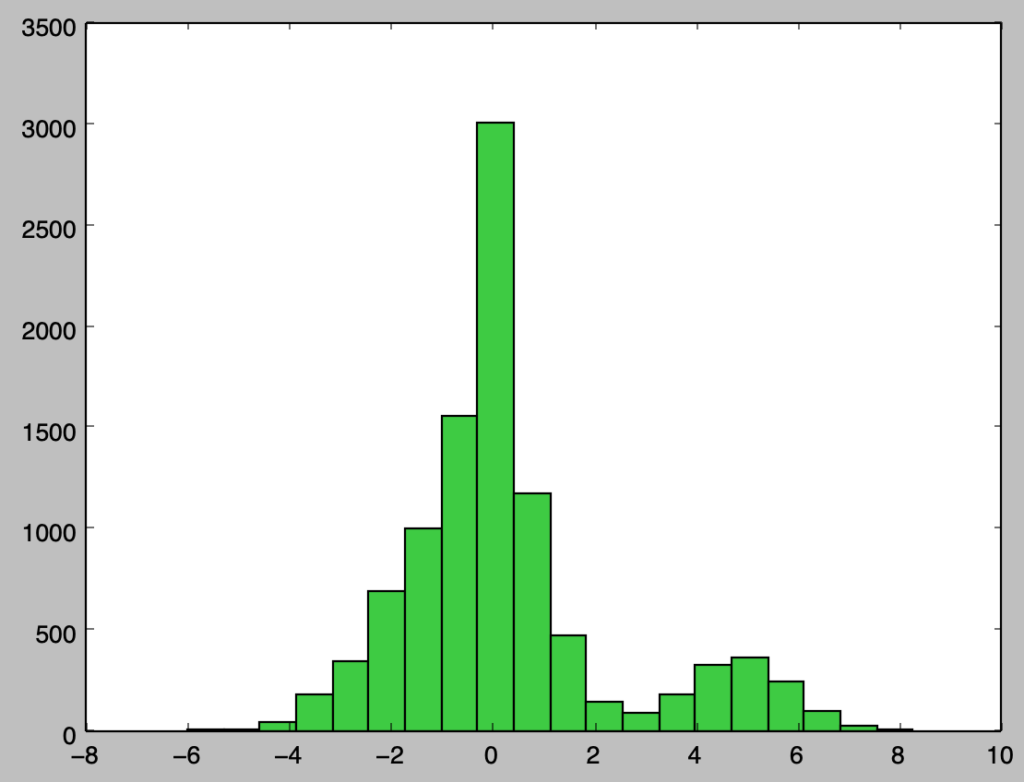
メトロポリスヘイスティングス法

ギブスサンプラー

発展的な手法

ハミルトニアンモンテカルロ法

下記で詳しく取り扱った。
・PyMC$3$、Pyroで学ぶ統計モデリング発展

NUTS(No U-Turn Sampler)