下記などで取り扱った、MCMCについて問題演習を通した理解ができるように問題・解答・解説をそれぞれ作成しました。
・標準演習$100$選
https://www.hello-statisticians.com/practice_100
Contents
基本問題
メトロポリス・ヘイスティングス法
ギブス・サンプリング
発展問題
最尤法・ベイズ推定・MCMCの活用
・問題
入門書などでのMCMC法の解説は通常の最尤法やベイズ推定と同時に取り扱われることが少ないので、この問題では以下、最尤法やベイズ推定と並行でMCMC法の基本的な流れを演習形式で具体的に確認を行う。下記の問いにそれぞれ答えよ。
i) ポアソン分布$\mathrm{Po}(\lambda)$に基づいて観測値$x_1,\cdots,x_n$が得られたと考えられる際に、パラメータ$\lambda$の推定を試みる。$x_1,\cdots,x_n$を元に尤度$L(\lambda)$を表せ。ポアソン分布の確率関数$p(x)$は下記のように表されることを用いて良い。
$$
\begin{align}
p(x) &= \frac{\lambda^{x} e^{-\lambda}}{x!} \\
&= \exp{(x \log{\lambda} – \lambda – \log{x!})}
\end{align}
$$
ⅱ) i)で確認を行なった尤度$L(\lambda)$を元に対数尤度$\log{L(\lambda)}$を計算し、$\lambda$で微分を行うことで$L(\lambda)$を最大にする$\lambda$を求めよ。
ⅲ) ⅱ)では最尤法に基づいて$\lambda$の点推定を行なったが、サンプルが少ない場合は$\lambda$の事前分布を元に事後分布を得るベイズ法を用いる場合が多い。ベイズ法を行う際にポアソン分布に基づく推定のようにシンプルな場合は共役事前分布を用いることで式変形に基づいて結果を得ることができる。
得られる観測値がポアソン分布に従う場合、パラメータ$\lambda$の共役事前分布はガンマ分布に従う。ガンマ分布$\mathrm{Ga}(\alpha,\beta)$の確率密度関数を変数$\lambda$に関して$f(\lambda)$とおくとき、$f(\lambda)$を表せ。
iv) パラメータ$\lambda$の事後分布を$P(\lambda|x_1,\cdots,x_n)$とおくとベイズの定理に基づいて$P(\lambda|x_1,\cdots,x_n) \propto L(\lambda)f(\lambda)$が成立する。i)とⅲ)の結果を用いて$P(\lambda|x_1,\cdots,x_n)$を計算し、$\lambda$の事後分布を答えよ。
v) ⅲ)、iv)ではパラメータ$\lambda$の共役事前分布$\mathrm{Ga}(\alpha,\beta)$を元に事後分布の導出を行なったが、実際は複雑な式を仮定することが多く共役事前分布が得られることが少ない。このような場合にMCMC法を用いる。
観測値$x_1=2, x_2=3, x_3=1$が得られた時、i)の式を目標分布、$\lambda$の初期値を$\lambda_0=2$、提案分布を$\lambda_{n+1} \sim \mathcal{N}(\lambda_{n},0.2^2)$とおく。このときMCMC法を用いて実際にサンプルを生成せよ。
・解答
i)
尤度$L(\lambda)$は下記のように表せる。
$$
\large
\begin{align}
L(\lambda) &= \prod_{i=1}^{n} p(x_i) \\
&= \prod_{i=1}^{n} \exp{(x_i \log{\lambda} – \lambda – \log{x_i!})} \\
&= \exp{\left( \sum_{i=1}^{n} (x_i \log{\lambda} – \lambda – \log{x_i!}) \right)}
\end{align}
$$
別解
下記のように表しても良い。
$$
\large
\begin{align}
L(\lambda) &= \prod_{i=1}^{n} p(x_i) \\
&= \prod_{i=1}^{n} \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} \\
&= \lambda^{\sum_{i=1}^{n} x_i} e^{-n \lambda} \left( \prod_{i=1}^{n} x_i! \right)^{-1}
\end{align}
$$
ⅱ)
対数尤度$\log{L(\lambda)}$は下記のように表せる。
$$
\large
\begin{align}
\log{L(\lambda)} &= \log{\left[ \exp{\left( \sum_{i=1}^{n} (x_i \log{\lambda} – \lambda – \log{x_i!}) \right)} \right]} \\
&= \sum_{i=1}^{n} (x_i \log{\lambda} – \lambda – \log{x_i!})
\end{align}
$$
上記を$\lambda$で偏微分を行うと下記が得られる。
$$
\large
\begin{align}
\frac{\partial \log{L(\lambda)}}{\partial \lambda} &= \frac{\partial}{\partial \lambda} \sum_{i=1}^{n} (x_i \log{\lambda} – \lambda – \log{x_i!}) \\
&= \sum_{i=1}^{n} \left( \frac{x_i}{\lambda} – 1 \right) \\
&= \frac{n(\bar{x}-\lambda)}{\lambda}
\end{align}
$$
上記の式変形にあたっては$\displaystyle \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$を用いた。上記が$\lambda$に関して単調減少であることから、$\lambda=\bar{x}$で$\log{L(\lambda)}$は最大値を取る。よって$L(\lambda)$を最大にする$\lambda$は$\lambda=\bar{x}$である。
ⅲ)
変数$\lambda$に関する確率密度関数$f(\lambda)$は下記のように表せる。
$$
\large
\begin{align}
f(\lambda) = \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \lambda^{\alpha-1} \exp{\left( -\frac{\lambda}{\beta} \right)}
\end{align}
$$
iv)
パラメータ$\lambda$の事後分布$P(\lambda|x_1,\cdots,x_n) \propto L(\lambda)f(\lambda)$は下記のように計算できる。
$$
\large
\begin{align}
P(\lambda|x_1,\cdots,x_n) & \propto L(\lambda)f(\lambda) \\
&= \lambda^{\sum_{i=1}^{n} x_i} e^{-n \lambda} \left( \prod_{i=1}^{n} x_i! \right)^{-1} \times \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \lambda^{\alpha-1} \exp{\left( -\frac{\lambda}{\beta} \right)} \\
& \propto \lambda^{\alpha + \sum_{i=1}^{n} x_i – 1} \exp{\left[ -\left( n+\frac{1}{\beta} \right) \lambda \right]} \\
&= \lambda^{\alpha + \sum_{i=1}^{n} x_i – 1} \exp{\left[ -\left( \frac{n \beta + 1}{\beta} \right) \lambda \right]} \\
&= \lambda^{\alpha + \sum_{i=1}^{n} x_i – 1} \exp{\left[ – \frac{\lambda}{\beta/(n \beta + 1)} \right]}
\end{align}
$$
よってパラメータ$\lambda$の事後分布はガンマ分布$\displaystyle \mathrm{Ga} \left( \alpha + \sum_{i=1}^{n} x_i , \frac{\beta}{n \beta + 1} \right)$である。
v)
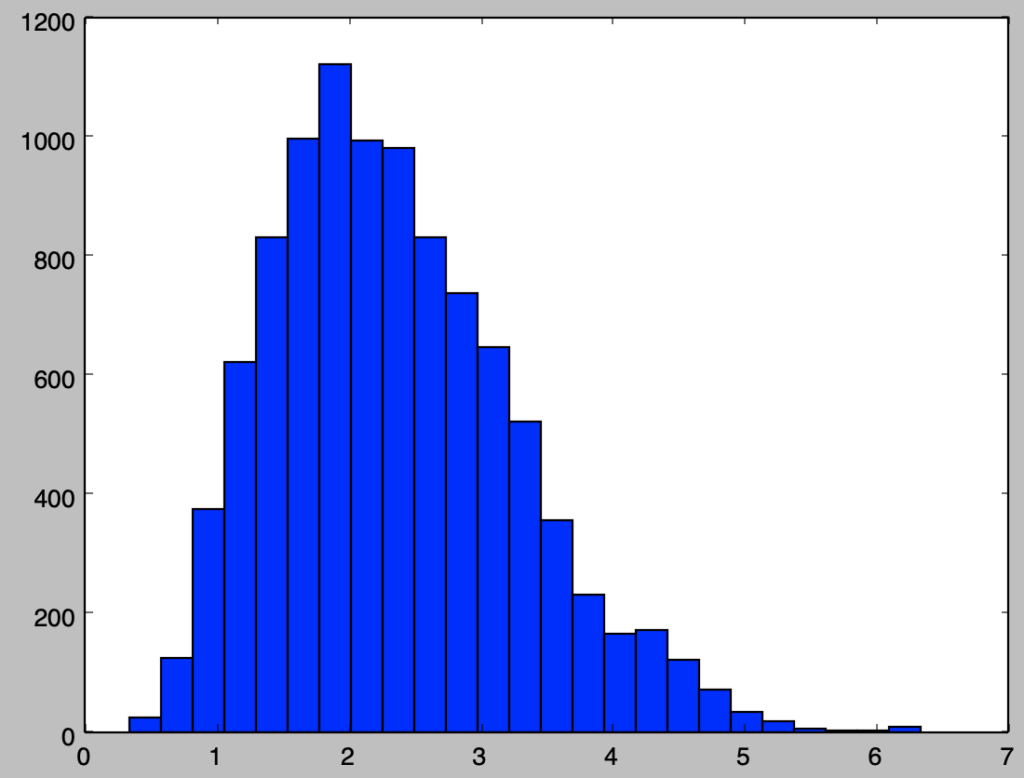
下記より、MCMC法に基づいてパラメータの分布を得ることができる。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
lamb = 2.
x = np.array([2., 3., 1.])
def calc_target_dist(lamb):
return lamb**(np.sum(x)) * np.e**(-x.shape[0]*lamb)
lambs = np.zeros(10000)
for i in range(11000):
y = stats.norm.rvs(0,0.2)
alpha = np.min([1.,calc_target_dist(lamb+y)/calc_target_dist(lamb)])
u = np.random.rand()
if alpha > u:
lamb = lamb+y
if (i+1)>1000:
lambs[i-1000] = lamb
plt.hist(lambs,bins=25)
plt.show()実行結果
・解説
下記などを参考に作成を行いました。
