統計検定1級 統計応用 問題解説 ～2019年11月実施 理工学 問1～

統計検定1級の2019年11月の「統計応用、理工学」の問1の解答例と解説について取り扱いました。他の問題の解答に関しては下記よりご確認ください。
https://www.hello-statisticians.com/stat_certifi_1_app

問題

詳しくは統計検定公式よりご確認ください。

日本統計学会公式認定 統計検定 1級・準1級 公式問題集［2018〜2019年］

3,300円(04/25 13:07時点)

Amazon

解答

$[1]$
累積分布関数$F(t)$、確率密度関数$f(t)=F'(t)$、生存関数$S(t)=1-F(t)$より、$f(t)$と$S(t)$に関して下記が成立する。
$$
\large
\begin{align}
f(t) &= \frac{d}{dt} F(t) = \frac{d}{dt} (1-S(t)) \\
&= – \frac{d}{dt} S(t)
\end{align}
$$

上記に基づいて$T$の期待値$\displaystyle E[T] = \int_{0}^{\infty} tf(t) dt$は下記のように変形を行うことができる。
$$
\large
\begin{align}
E[T] &= \int_{0}^{\infty} tf(t) dt \\
&= \left[ -t S(t) \right]_{0}^{\infty} + \int_{0}^{\infty} S(t) dt \\
&= \int_{0}^{\infty} S(t) dt
\end{align}
$$

これより、$\displaystyle E[T] = \int_{0}^{\infty} S(t) dt$を示すことができる。また、上記の計算にあたっては$\displaystyle \lim_{n \to \infty} tS(t)=0$を用いた。

$[2]$
・$\displaystyle m(t) = \frac{\int_{t}^{\infty} S(x) dx}{S(t)}$の導出
下記のように数式変形を行うことができる。
$$
\large
\begin{align}
\int_{t}^{\infty} S(x) dx &= \left[ xS(x) \right]_{t}^{\infty} + \int_{t}^{\infty} x f(x) dx \\
&= -t S(t) + S(t) \int_{t}^{\infty} x \frac{f(x)}{S(t)} dx \\
&= S(t) \left[ \int_{t}^{\infty} x \frac{f(x)}{S(t)} dx – t \right] \\
&= S(t) (E[T|T>t] – t) \\
&= S(t) E[T-t|T>t] = S(t) m(t)
\end{align}
$$

上記より、$\displaystyle m(t) = \frac{\int_{t}^{\infty} S(x) dx}{S(t)}$が成立することが示せる。

・$\displaystyle m(t) = \int_{0}^{\infty} \exp \left[ H(t) – H(t+x) \right] dx$の導出
$\displaystyle h(t) = – \frac{t}{dt} \log{S(t)}$より、$H(t) = – \log{S(t)}$が成立する。これより$\displaystyle \int_{0}^{\infty} \exp \left[ H(t) – H(t+x) \right] dx$は下記のように変形できる。
$$
\large
\begin{align}
\int_{0}^{\infty} \exp \left[ H(t) – H(t+x) \right] dx &= \int_{0}^{\infty} \exp \left[ – \log{S(t)} + \log{S(t+x)} \right] dx \\
&= \int_{0}^{\infty} \exp \left[ \frac{S(t+x)}{S(t)} \right] dx \\
&= \frac{1}{S(t)} \int_{0}^{\infty} \exp [ S(t+x) ] dx \\
&= \frac{1}{S(t)} \int_{t}^{\infty} \exp [ S(y) ] dy \\
&= E[T-t|T>t] = m(t)
\end{align}
$$

上記より、$\displaystyle m(t) = \int_{0}^{\infty} \exp \left[ H(t) – H(t+x) \right] dx$が成立することがわかる。

・$\displaystyle S(t) = \exp \left[ – \int_{0}^{t} \frac{1+m'(x)}{m(x)} \right]$の導出
$\displaystyle \int_{t}^{\infty} S(x) dx = m(t)S(t)$の両辺を$t$で微分し、整理すると下記のように変形を行うことができる。
$$
\large
\begin{align}
\frac{d}{dt} \left( \int_{t}^{\infty} S(x) dx \right) &= \frac{d}{dt} \left( m(t)S(t) \right) \\
-S(t) &= m'(t)S(t) + m(t)S'(t) \\
-m(t)S'(t) &= S(t) + m'(t)S(t) \\
-m(t)S'(t) &= (1 + m'(t))S(t) \\
\frac{S'(t)}{S(t)} &= -\frac{1+m'(t)}{m(t)}
\end{align}
$$

上記の両辺を$0$から$t$の区間で積分すると下記が得られる。
$$
\large
\begin{align}
\int_{0}^{t} \frac{S'(x)}{S(x)} dx &= -\int_{0}^{t} \frac{1+m'(x)}{m(x)} dx \\
\left[ \log{S(x)} \right]_{0}^{t} &= -\int_{0}^{t} \frac{1+m'(x)}{m(x)} dx \\
\log{S(t)} &= -\int_{0}^{t} \frac{1+m'(x)}{m(x)} dx
\end{align}
$$

$[3]$
$(1)$
$$
\large
\begin{align}
h(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T \leq t + \Delta t | T \geq t)}{\Delta t}
\end{align}
$$
上記の数式で表されるように、ハザード関数$h(t)$は$t$まで稼働していた製品が$t$で故障する瞬間故障率を表す。

$(2)$
累積ハザード関数$H(t)$が凸関数であることは$H(t)$の$1$階微分であるハザード関数$h(t)$の微分が増加関数であることを表す。同様に$H(t)$が凹関数であることは$h(t)$が減少関数であることを表す。

$[4]$
$(1)$
$g_{\beta}(t)$の累積分布関数$G_{\beta}(t)$とおくと、$T=X^{1/\beta}$より$G_{\beta}(t)$は下記のように表すことができる。
$$
\large
\begin{align}
G_{\beta}(t) &= P(T \leq t) = P(X^{1/\beta} \leq t) \\
&= P(X \leq t^{\beta}) = F(t^{\beta}) = 1 – e^{-t^{\beta}}
\end{align}
$$

上記より、$g_{\beta}(t)$は下記のように導出できる。
$$
\large
\begin{align}
g_{\beta}(t) &= \frac{d}{dt} G_{\beta}(t) \\
&= \beta t^{\beta-1} e^{-t^{\beta}}
\end{align}
$$

次に、$S_{\beta}(t)=1-G_{\beta}(t)=e^{-t^{\beta}}$より、ハザード関数$h_{\beta}(t)$は下記のようになる。
$$
\large
\begin{align}
h_{\beta}(t) &= \frac{g_{\beta}(t)}{S_{\beta}(t)} \\
&= \frac{\beta t^{\beta-1} e^{-t^{\beta}}}{e^{-t^{\beta}}} = \beta t^{\beta-1}
\end{align}
$$

また、ここで$h_{\beta}(t)=\beta t^{\beta-1}$より、$\beta>1$で分布はIFR、$\beta<1$でDFRとなることがわかる。$\beta=1$の場合はIFRかつDFRでこれは指数分布に一致する。

・別解
$g_{\beta}(t)$は確率密度関数の変数変換の考え方を用いて導出することもできる。

$(2)$
$h_{1/2}(t), h_{2}(t)$はそれぞれ下記のように表される。
$$
\large
\begin{align}
h_{1/2}(t) &= \frac{1}{2} t^{-1/2} \\
h_{2}(t) &= 2t
\end{align}
$$

これらのグラフは下記のように描くことができる。

import numpy as np
import matplotlib.pyplot as plt

t = np.arange(0,3,0.01)
h_1_2 = t**(-0.5) / 2.
h_2 = 2*t

plt.plot(t,h_1_2)
plt.plot(t,h_2)

plt.show()

・実行結果

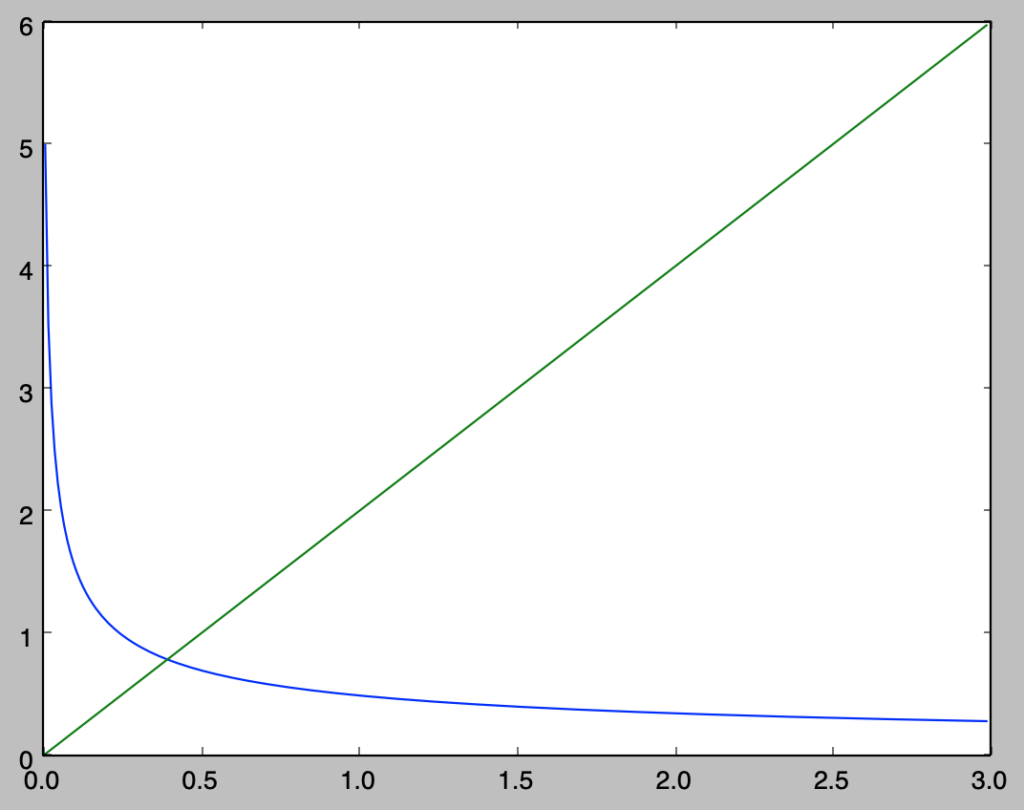
解説

ハザード関数はよく出題されるので、抑えておくと良いと思います。また、$[4]$の$(1)$のような変数変換では確率密度関数の変数変換を用いて導出することもできますが、累積分布関数、生存関数、ハザード関数などが出てくる際は累積分布関数から考えた方がシンプルだと思います。