強化学習まとめ① 〜有限マルコフ決定過程(Finite MDP)〜

強化学習(Reinforcement Learning)は数式が多く一見難しそうに見えますが、統計学の確率分布の表記に慣れていれば実はそれほど難しくありません。そこで何回かにわけて強化学習の基本トピックに関して取り扱いを行います。
第$1$回は強化学習の問題設定を理解するにあたって「有限マルコフ決定過程(Finite Markov Decision Process)」を取り扱います。Richard S. Suttonの”Reinforcement Learning, second edition: An Introduction“のChapter$3$を参考に作成を行いました。

基本的な理論の確認

MDPの概要

有限マルコフ決定過程(Finite Markov Decision Process)は逐次的意思決定(sequential decision making)のよく用いられてきた定式化である。

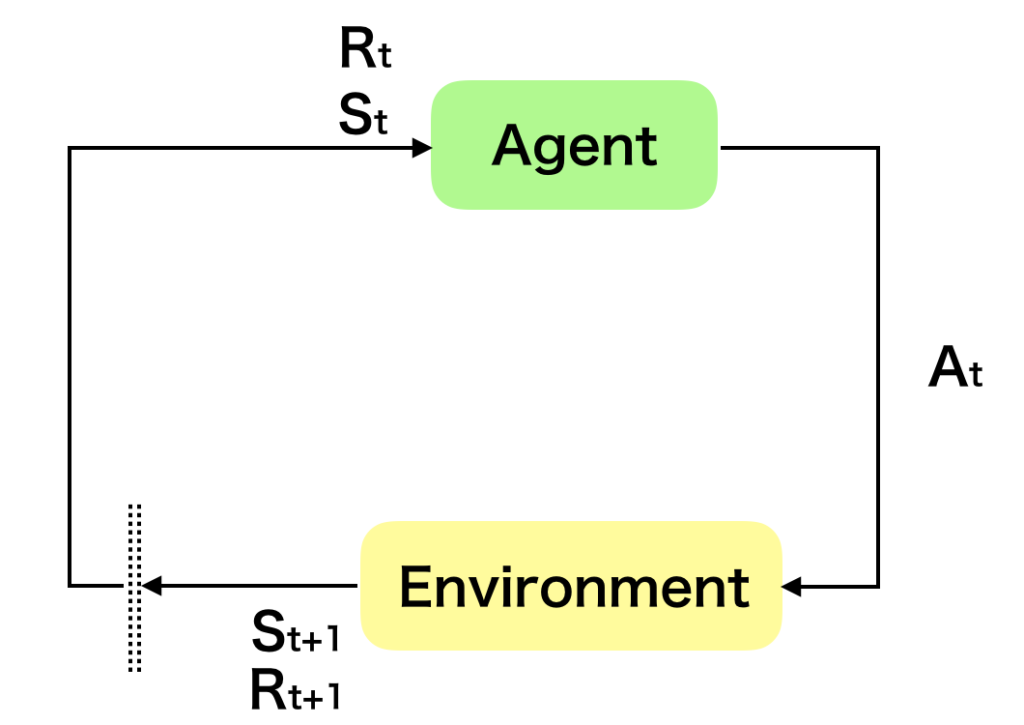
強化学習の図式化では上のような図がよく用いられるが、これは逐次的意思決定問題の$1$ステップを切り抜いたものであると理解すると良い。エージェント(Agent)が環境(Environment)から状態$S_t$と報酬$R_t$を観測し、行動$A_t$を行うことで次の状態$S_{t+1}$と次の報酬$R_{t+1}$を観測するというのが一連の流れである。ここで$S_{t}$に対して$A_{t}$を実行した際の報酬を$R_t$と定義するか$R_{t+1}$と定義するかは議論の余地があるように思われるが、参照した”Reinforcement Learning, second edition: An Introduction”では$R_{t+1}$を用いているので以下では$R_{t+1}$を用いる。

このように状態$S_t$、報酬$R_t$、行動$A_t$を定義し、実際に一連のプロセスを実行すると下記のような系列(trajectory)が得られる。
$$
\large
\begin{align}
S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, …
\end{align}
$$

上記のように考える場合、行列形式で系列を保存することが難しいならば、$R_0=0$とおいて$R_0, S_0, A_0, …$とすることもできると考えられる。また、$S_t, A_t, R_t$はそれぞれ集合表記を用いて下記のように表すことができることも抑えておくと良い。
$$
\large
\begin{align}
S_{t} & \in \mathcal{S} \\
A_{t} & \in \mathcal{A} \\
R_{t} & \in \mathcal{R} \subset \mathbb{R}
\end{align}
$$

状態遷移確率と方策

強化学習を考える上で数式が難しくなりがちなのが状態遷移確率(state-transition probabilities)と方策(policy)である。どちらもエージェントの行動に基づいて状態が遷移する際に用いられる確率分布であるが、「方策」が状態に対するエージェントの行動の確率分布である一方で、「状態遷移確率」はエージェントの行動を受けて環境が状態を変化させるときの確率分布であることは抑えておく必要がある。

方策$\pi(a|s)$は確率分布を表す$P$を用いて下記のように表すことができる。
$$
\large
\begin{align}
\pi(a|s) = P(A_t=a|S_t=s)
\end{align}
$$

また、状態遷移確率$p(s’,r|s,a)$は同様に$P$を用いて下記のように表すことができる。
$$
\large
\begin{align}
p(s’,r|s,a) = P(S_{t+1}=s’,R_{t+1}=r|S_t=s,A_{t}=a)
\end{align}
$$

状態遷移確率$p(s’,r|s,a)$と方策$\pi(a|s)$は価値関数を定義する際にどちらも出てくるのでそれぞれ抑えておく必要がある。方策はエージェント、状態遷移確率は環境が持つ確率分布であると把握しておくとわかりやすいと思われる。

エピソードと報酬和(return)

強化学習の目的は一連の逐次的意思決定$S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, …$が完了するまでの獲得報酬を最大化することにある。この一連の意思決定$1$回の単位はエピソード(episode)とされることが多い。

$1$エピソードにおける$t$以降の報酬の和$G_{t}$を下記のように定義することを考える。
$$
\large
\begin{align}
G_{t} & \equiv R_{t+1} + \gamma R_{t+2} + … \\
&= \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \quad (1)
\end{align}
$$

上記の$\gamma$は$0 \leq \gamma \leq 1$を定義域に取り、割引率(discount rate)と呼ばれる。割引率は即時(immediate)に得られる報酬を将来的に得られる報酬よりも重視するという考え方である。

また、$G_{t}$に関して下記のような変形を行うことができる。
$$
\large
\begin{align}
G_{t} & \equiv R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + … \\
&= R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + … ) \\
&= R_{t+1} + \gamma (R_{(t+1)+1} + \gamma R_{(t+1)+2} + … ) \\
&= R_{t+1} + \gamma \sum_{k=0}^{\infty} \gamma^{k} R_{(t+1)+k} \\
&= R_{t+1} + \gamma G_{t+1} \quad (2)
\end{align}
$$

上記で表した$(2)$は数列における漸化式と同様に理解すると良い。$(1)$式、$(2)$式はそれぞれ、数列${ a_{n} }$の$a_{n}$和を$S_{n}$のようにおいた際の下記の式にそれぞれ対応する。
$$
\large
\begin{align}
S_{n} &= \sum_{n}^{\infty} a_x \quad (1)’ \\
S_{n} &= \sum_{n}^{\infty} a_x = a_{n} + a_{n+1} + … \\
&= a_{n} + (a_{n+1} + a_{n}+2 + …) = a_{n} + \sum_{n+1}^{\infty} a_x \quad (2)’
\end{align}
$$

価値関数(value function)・ベルマン方程式(Bellman equation)

強化学習のほぼ全てのアルゴリズムは価値関数(value function)の推定に関係する。

価値関数は状態の価値(how good)を評価する関数だが、状態の価値は以後の報酬和の期待値(expected return)の点から定義される。

方策$\pi(a|s)$に対応する状態$s$の状態価値関数(state-value function)を$v_{\pi}(s)$とおくと、$v_{\pi}(s)$は下記のように定義される。
$$
\large
\begin{align}
v_{\pi}(s) & \equiv \mathbb{E}_{\pi} [G_{t}|S_{t}(s)] \\
&= \mathbb{E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \Bigr| S_{t}=(s) \right], \quad s^{\forall} \in \mathcal{S} \quad (3)
\end{align}
$$

また、状態$s$の価値と同様に状態$s$における行動$a$の価値を計算できると良い場合も多い。よって、状態$s$における行動$a$の価値を表す行動価値関数(action-value function)を$q_{\pi}(s,a)$とおき、下記のように定義される。
$$
\large
\begin{align}
q_{\pi}(s,a) & \equiv \mathbb{E}_{\pi} [G_{t}|S_{t}(s)] \\
&= \mathbb{E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \Bigr| S_{t}=(s),A_{t}=(a) \right]
\end{align}
$$

$(3)$式は前項で取り扱った報酬和に関する変形に基づいて下記のように変形を行うことができる。
$$
\large
\begin{align}
v_{\pi}(s) &= \mathbb{E}_{\pi} [G_{t}|S_{t}(s)] \\
&= \mathbb{E}_{\pi} [R_{t+1} + \gamma G_{t+1}|S_{t}(s)] \\
&= \sum_{a} \pi(a|s) \sum_{s’,r} p(s’,r|s,a) \left[ r + \gamma v_{\pi}(s’) \right], \quad s^{\forall} \in \mathcal{S}
\end{align}
$$

上記を$v_{\pi}$に関するベルマン方程式(Bellman equation)という。

最適方策・最適状態価値関数

強化学習の目的は推定した価値関数などを元に報酬を最大化する方策を見つけることにある。これを最適方策(optimal policy)と定義する。

ここで方策$\pi_{*}$が最適方策であるということは、全ての状態$s$に対して下記が成立することに対応する。
$$
\large
\begin{align}
v_{\pi_{*}}(s) \geq v_{\pi}(s), \quad s^{\forall} \in \mathcal{S}
\end{align}
$$

最適方策に対応する状態価値関数を最適状態価値関数(optimal state-value function)という。ここで、最適状態価値関数を$v_{*}$と定めるとき、$v_{*}(s)$は下記のように表すことができる。
$$
\large
\begin{align}
v_{*}(s) = v_{\pi_{*}}(s) = \max_{\pi} v_{\pi}(s)
\end{align}
$$

上記の数式の解釈にあたっては$\displaystyle \max_{\pi} v_{\pi}(s)$が$v_{\pi}(s)$を最大化する$\pi$に基づく$v_{\pi}(s)$の値を表すことは抑えておくと良い。

また、最適方策に対応する行動価値関数を最適行動価値関数(optimal action-value function)という。ここで、最適行動価値関数を$q_{*}$と定めるとき、$q_{*}(s,a)$は下記のように表すことができる。
$$
\large
\begin{align}
q_{*}(s,a) = q_{\pi_{*}}(s,a) = \max_{\pi} q_{\pi}(s,a)
\end{align}
$$

具体例の確認