データの可視化(data visualization)は、データを様々な角度から確認し、データ自体を理解する目的で行われることが多い印象です。探索的データ分析(EDA)と呼ばれることもあります。pythonを使ってデータを可視化する際に、手軽に静的なデータの可視化ができるライブラリとしてmatplotlibがよく使われていると思います。ここでは、matplotlibで手軽にデータを可視化するために覚えておくと良いと思われる基礎的な項目をまとめます。
Contents
matplotlib
matplotlibは、pythonにおけるデータ可視化のためのライブラリです。matplotlibを利用すると、簡潔に様々なグラフをプロットできます。主に静的なグラフのプロットに使われることが多い印象です。詳細なドキュメント以下の公式ドキュメントを参照してください。
matplotlibの導入
インストール
インストールについては、公式ドキュメントで解説されています。特にこだわりがなければ、pipを使ってインストールできます。
> pip install matplotlibmatplotlibの始めの一歩
matplotlibを利用したシンプルな例を紹介します。
import matplotlib.pyplot as plt
x = [0, 1, 2, 3, 4, 5]
y = [0, 2, 1, 3, 2, 4]
plt.plot(x, y)
plt.show()このコードを実行すると以下のグラフがプロットされます。
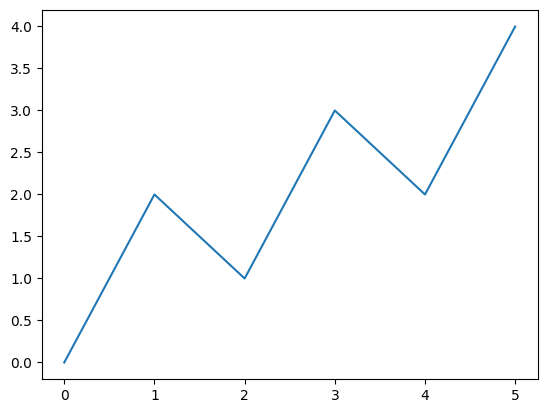
ここで重要なポイントは、以下で説明する2点です。
ライブラリのimport
import matplotlib.pyplot as pltこの文で、matplotlibのpyplotモジュールをpltという名前でインポートしています。pyplotモジュールというのは、matplotlibにおけるグラフ描画のためのインターフェースです。pyplotモジュールの配下に散布図やヒストグラムなどを描画するための関数が用意されています。
pyplotモジュールについては後述の「matplotlibでの描画方針」に追加で説明を記載します。
プロットの実行
plt.plot(x, y)この文で折れ線グラフを描画しています。matplotlib.pyplotではこのように、描画したいグラフに対応する関数を呼び出すだけでグラフを描画することが出来ます。
matplotlibでの描画方針
matplotlibでグラフを描画するには以下の二つの方針があります。
- グラフ要素のオブジェクトを生成してグラフ描画していく方針(object-oriented interface)
- pyplotモジュールを利用して予め用意された関数を利用してグラフ描画をしていく方針(state-based interface)
1のobject-orientedな方針では、グラフ描画にあたって細かい指定ができるのですが、その分コードは複雑になります。2のstate-basedな方針では、matplotlibのpyplotモジュールで提供されている関数を呼び出すだけなので簡単に描画を実行できます。
本稿では、基本的には2の方針での解説を行います。ですが、複数のグラフを1枚にまとめる(subplot)などでオブジェクト思考的な利用をすることがあります。
matplotlibでの描画要素
matplotlibにおける描画要素(描画オブジェクト)は、pyplotモジュールを単純に利用するだけの場合はあまり意識する必要はありません。しかし、軸の調整や複数グラフをまとめる場合などで意識しておくとより理解が深まります。
このmatplotlibにおけるオブジェクトを理解する上で公式ドキュメントにある図(こちらを参照)がとてもわかりやすいです。ただ、基礎を理解するという視点では、少々複雑なので、必要な要素を抽出すると、以下の3点を覚えておくと良いです。
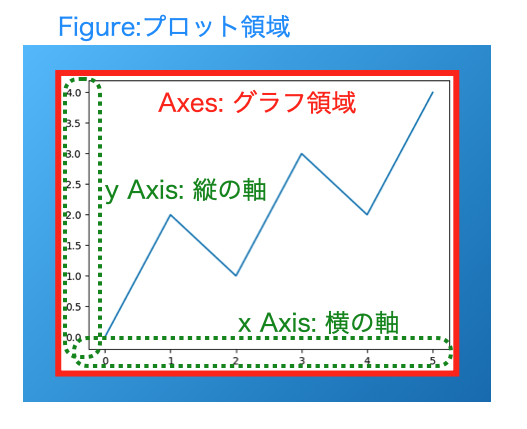
- Figure: グラフをプロットする全体の領域。ここに下記のAxesオブジェクトを配置していくイメージ。
- Axes: グラフ自体。Figureの中に複数のAxesを配置することが可能。
- Axis: 軸。軸の大きさや表示範囲、スケールなどを定義する。AxesとAxis紛らわしいが別物なので注意。
基本的なグラフ描画
散布図
| プロットの概要 | 縦軸と横軸にそれぞれ対応する量を割り当て、データを点でプロットしたもの。 |
| プロットから主に確認できるポイント | 縦軸と横軸に割り当てた量の相関関係。2次元のデータの分布。 |
| 向いているデータ | データの順番に意味がないデータ(独立なデータ) |
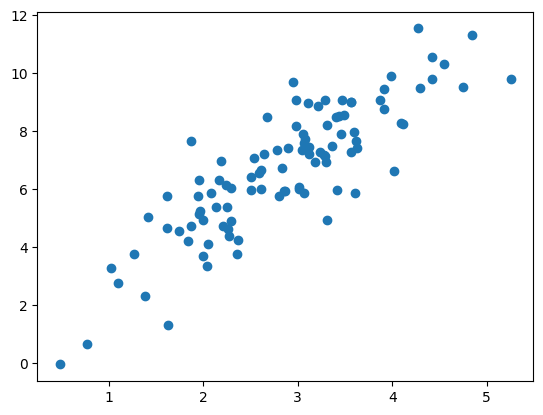
例として、y=2x+1に従ってランダムノイズが加わった線型モデルからランダムにサンプルしたデータを散布図で確認してみます。
N = 100
x = np.random.randn(N) * 1.0 + 3.0 # N(3, 1)からランダムに生成
y = 2. * x + 1 + np.random.randn(N)
plt.scatter(x, y)上記コードを実行すると以下のような図が作成されます。
折れ線グラフ
| プロットの概要 | 散布図の一種で、データ間を線で結んだもの。 横軸に設定する量を基準にデータを並べることが多い。 |
| プロットから主に確認できるポイント | 時間経過での変化など、データがどのように変わっていったかを確認できる。 |
| 向いているデータ | 時系列データに代表される、データ間の順番に意味のあるデータ |
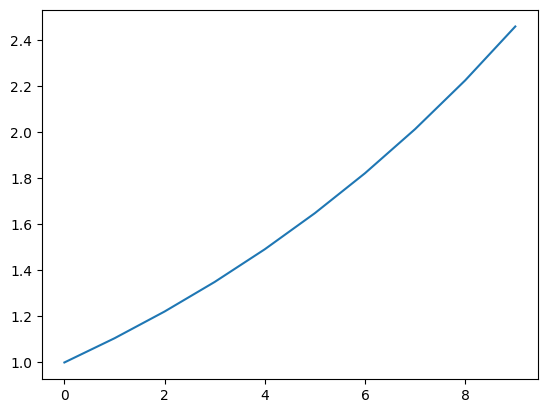
例として、横軸(時間)に対して指数関数に従って値が上昇していくようなデータをプロットして確認してみます。
t = np.arange(0, 10)
y = np.exp(0.1 * t)
plt.plot(t, y)上記コードを実行すると以下のような図が作成されます。
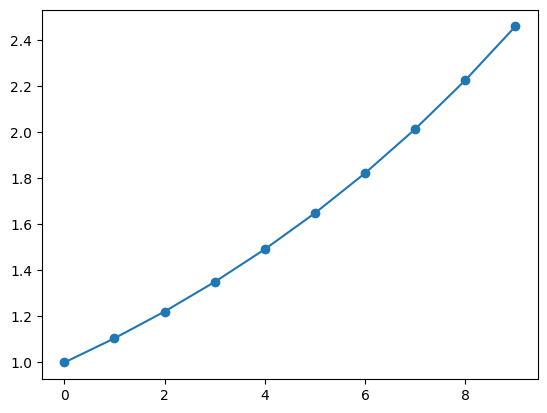
折れ線グラフでは、データポイントを明示するように記号をつけることも多いです。下記のようにpyplt.plotのオプションを設定することで実現できます。
t = np.arange(0, 10)
y = np.exp(0.1 * t)
plt.plot(t, y, "-o")コード例では、pyplot.plot の3つ目の引数として、フォーマットを指定しています。このフォーマットで線の色なども設定できます。詳しくはドキュメントを参照してください。
棒グラフ
| プロットの概要 | データの大きさを棒(長方形)の高さで表現したグラフ。 横軸には特に既定はないが、カテゴリ(質的)データを使うことが多い印象(e.g. 営業員毎の売り上げなど)。 |
| プロットから主に確認できるポイント | 横軸に設定する値ごとの量の比較 |
| 向いているデータ | 質的なデータとその量 |
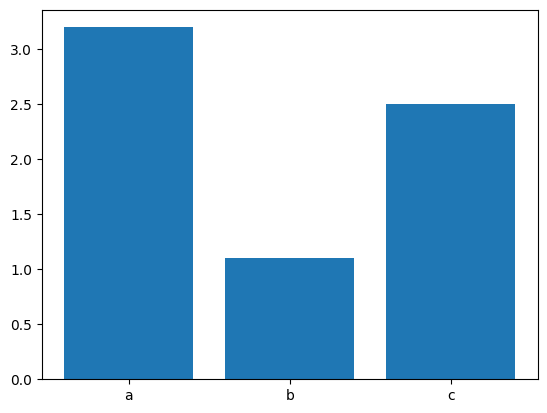
例として、3つのカテゴリの量を比較する棒グラフを描いてみます。
x = np.array(["a", "b", "c"])
y = np.array([3.2, 1.1, 2.5])
plt.bar(x, y)上記コードを実行すると以下のような図が作成されます。
ヒストグラム
| プロットの概要 | 度数分布表の度数を棒の高さで表現したグラフ。横軸には階級をとる。 |
| プロットから主に確認できるポイント | データの分布状況を可視化する。 |
| 向いているデータ | 1次元の数量データ |
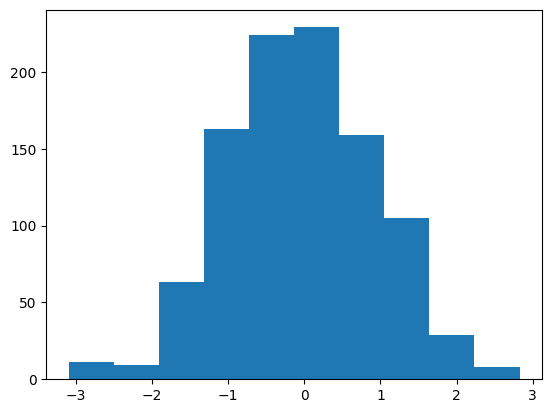
例として、正規分布に従う乱数のヒストグラムを描いてみます。
x = np.random.randn(1000) * 1.0 + 0.0
plt.hist(x)上記コードを実行すると以下のような図が作成されます。
ヒストグラムにとって、横軸(階級)は重要です。階級の幅を適切に設定しないとデータの解釈をミスリードする場合があります。例えば、上記のヒストグラムの階級幅を細かく設定してみます。matplotlibでは、pyploy.hist のbins に数値を設定するとデータの最大最小範囲を設定した値で均等に分割してくれます。
plt.hist(x, bins=100)上記コードを実行すると以下のような図が作成されます。
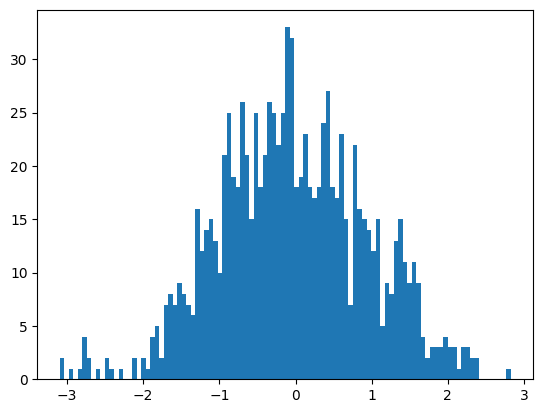
単純な標準正規分布$\mathcal{N}\left(0, 1 \right)$から乱数を生成したのですが、上記の図ではいくつか山があるように見えないこともないですよね。適切な解像度でデータを確認しないとノイズに過度に適合してしまうデータ解釈をしてしまうことがあります。
なお、pyploy.hist のbins にlistやnumpy.arrayなどを設定すると、任意の階級を設定することができます。
グラフの修飾
色の変更
軸の変更
スケール、描画範囲、対数軸
日本語の利用
日本語などの文字を利用したい場合、フォントを指定する必要があります。matplotlibで日本語フォントを利用するには複数の方法があります(下記)。
- 設定ファイルを作成してフォントを指定する
- 日本語フォントに対応したFontPropertyを作成し、日本語を使う箇所で都度指定する
- japanize-matplotlibを利用する
1と2の方法は似ていますが、1の方法では予め設定ファイルを作成し、その中でデフォルトフォントを設定します。2の方法では、ソースコード単位でFont Propertyを作成します。3の方法ではmatplotlibを日本語化するライブラリが公開されており、そちらを利用する方法です。3の方法が最も手間が少なく簡単だと思います。
ここでは、2の方法について、フォントファイルの入手から手順を解説します。
まずフォントファイルのダウンロードと展開をします。フォントファイルはシステムにインストールされているフォントファイルを使っても良いですが、Linux環境などシステムフォントがインストールされていないケースもあると思います。
wget https://moji.or.jp/wp-content/ipafont/IPAexfont/ipaexg00401.zip
unzip ipaexg00401.zip上記の例では、ターミナルでのコマンド実行を想定していますが、jupyterlabなどから実行する場合には、システムコマンドを利用するために各文の先頭に ! をつけます。
FontPropertyの作成と利用について、以下に例を示します。
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
font_path = './ipaexg00401/ipaexg.ttf'
fp = fm.FontProperties(fname=font_path)
x = [0, 1, 2, 3, 4, 5]
y = [0, 2, 1, 3, 2, 4]
plt.plot(x, y, label="日本語描画の例")
plt.title("日本語タイトル", fontproperties=fp)
plt.legend(prop=fp)
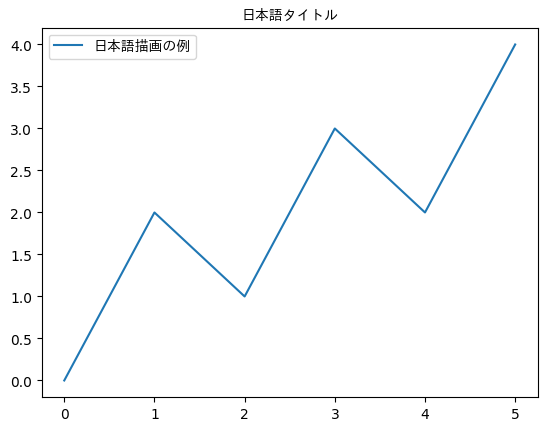
plt.show()上記のコードを実行すると、以下の図が出力されます。
上記のコードにおける重要なポイントを解説します。
import matplotlib.font_manager as fm
font_path = './ipaexg00401/ipaexg.ttf'
fp = fm.FontProperties(fname=font_path)matplotlib.font_manager.FontPropertiesにフォントファイルを指定します。これで指定したフォントファイルを使うことが出来ます。なおこの例にあるように、フォントファイルはどこに展開したものでも構いません。フォントなどのインストールが自由に出来ない環境などに有効だと思います。
plt.plot(x, y, label="日本語描画の例")
plt.title("日本語タイトル", fontproperties=fp)
plt.legend(prop=fp)plotのlabelとタイトルに日本語を利用しています。フォントを指定しない場合、日本語が表示できず四角で置き換わってしまうと思いますが、上図の通り、日本語表示できるようになっています。
pyplot.titleとpyplot.legendでフォントを指定するオプショナル引数が異なっているので注意してください。
[参考]
応用的な利用方法
3次元のデータの可視化
scatterplot, heatmap
複数のグラフをまとめる
1枚のFigureに複数のグラフをまとめたいケースはいくつか考えられると思います。このような場合、pyplotのsubplots関数を利用すると比較的容易に実現できます。複数のグラフをどのように配置するかという考え方については、上記「matplotlibでの描画要素」におけるFigure要素とAxes要素を意識すると良いです。
まず具体例を以下に示します。
x = np.random.randn(100) * 1.0 + 3.0 # N(3, 1)の分布から50個のデータを取得
y = 2. * x + 0.5
z = y + np.random.randn(100)
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs[0].hist(x)
axs[1].scatter(x, z)
fig.show()上記のコードを実行すると、以下の図が出力されます。なお乱数を利用しているため、実行毎に結果は変わります。
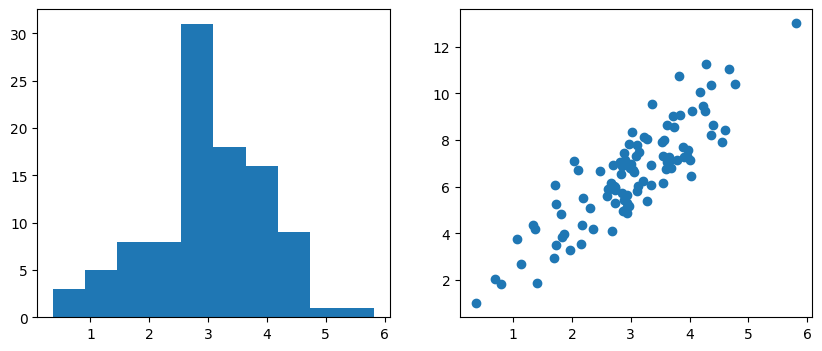
上記のコードにおける重要なポイントを解説します。
fig, axs = plt.subplots(1, 2, figsize=(10, 4))まずここで、pyplot.subplotsを呼び出し、グラフを描画するFigure要素とAxes要素のオブジェクトを生成します。この時、subplotsの第1引数として行数(nrows)、第2引数に列数(ncols)を指定しているので、axsには二つのAxesオブジェクトのリストが返ってきます。
axs[0].hist(x)
axs[1].scatter(x, z)二つのAxesオブジェクトそれぞれで、ヒストグラム(hist)と散布図(scatter)を描画しています。
[参考]
軸(Axis)を共有して複数のグラフをまとめる
一つのFigureに独立したグラフを並べるだけでは、複数のグラフをそれぞれ描画するのと変わりません。ここでは、複数のグラフの軸のを合わせて描画する方法について解説します。
まず、具体例を示します。
x1 = np.random.randn(500) * 1.0 + 0.0 # N(0, 1)の分布から500個のデータを取得
x2 = np.random.randn(500) * 2.0 + 5.0 # N(5, 2)の分布から500個のデータを取得
fig, axs = plt.subplots(2, 1, sharex=True)
axs[0].hist(x1)
axs[1].hist(x2)
fig.show()上記のコードを実行すると、以下の図が出力されます。なお乱数を利用しているため、実行毎に結果は変わります。
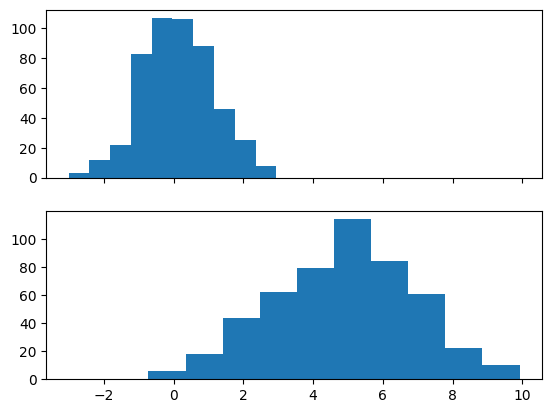
上記のコードにおける重要なポイントを解説します。
fig, axs = plt.subplots(2, 1, sharex=True)pyplot.subplotsのオプショナル引数である sharex=True を指定しています。これで、二つのグラフにおけるx軸が共有されたことになります。同様に、y軸を共有するには sharey=True を指定します。
[参考]
まとめ
参考
- 統計学を学ぶにあたって知っておくと良いMatplotlibの用法
- 1問1答形式でmatplotlibの事例を解説