数学検定2級 解説　〜過去問題① 解答例・解説　1次：計算技能検定・2次：数理技能検定〜

数学検定$2$級は数ⅡBまで相当の数学の基本トピックに関して取り扱った検定であり、統計学に必要な数学を身につける際の目安になります。当記事では「日本数学検定協会 監修」の「数学検定問題集 $2$級」の数学検定$2$級の内容に基づき、過去問題①の解答例と解説の作成を行いました。

・数学検定$2$級まとめ
https://www.hello-statisticians.com/math_certificate_2

$1$次：計算技能検定

問題$1 \,$ 多項式の展開

下記のように式の展開を行うことができる。
$$
\large
\begin{align}
(x^2-1)(1+x^2+x^4+x^6) &= (\cancel{x^2}+\cancel{x^4}+\cancel{x^6}+x^8) – (1+\cancel{x^2}+\cancel{x^4}+\cancel{x^6}) \\
&= x^8 – 1
\end{align}
$$

・参考
$(A-B)(A^2+AB+B^2)=A^3-B^3$と同様な式であることは抑えておくと良い。

問題$2 \,$ 因数分解

下記のように因数分解を行うことができる。
$$
\large
\begin{align}
x^3 – \frac{3}{10}x^2y + \frac{3}{100}xy^2 – \frac{1}{1000}y^3 &= x^3 – 3x^2\left( \frac{y}{10} \right) + 3x\left( \frac{y}{10} \right)^2 – \left( \frac{y}{10} \right)^3 \\
&= \left( x – \frac{y}{10} \right)^3
\end{align}
$$

問題$3 \,$ 展開の公式と分数関数

$\displaystyle x-\frac{1}{x}=3$より、$\displaystyle \left( x-\frac{1}{x} \right)^2=9$が成立し、下記のように変形できる。
$$
\large
\begin{align}
\left( x-\frac{1}{x} \right)^2 &= 9 \\
x^2 + \frac{1}{x^2} – 2 x \cdot \frac{1}{x} &= 9 \\
x^2 + \frac{1}{x^2} &= 11
\end{align}
$$

問題$4 \,$ 三角比と三角形の面積

面積を$S$とおくと三角形の公式に基づいて下記のように計算できる。
$$
\large
\begin{align}
S &= \frac{1}{2} \times 8 \times 5 \sin{60^{\circ}} \\
&= \frac{1}{2} \times 8 \times 5 \times \frac{\sqrt{3}}{2} \\
&= 10 \sqrt{3}
\end{align}
$$

問題$5 \,$ 組み合わせ

$10$人から赤組$5$人を選ぶ組み合わせ${}_{10} C_{5}$を計算すれば良い。
$$
\large
\begin{align}
{}_{10} C_{5} &= \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6}{5!} \\
&= 252
\end{align}
$$

よって$252$通りの分け方が存在する。

問題$6 \,$

問題$7 \,$ 三角関数の倍角の公式と二次方程式

$[1]$
$\cos{2 \theta} = \sin{\theta}$は下記のように解くことができる。
$$
\large
\begin{align}
\cos{2 \theta} &= \sin{\theta} \\
\cos^{2}{\theta}-\sin^{2}{\theta} &= \sin{\theta} \\
(\cos^{2}{\theta}+\sin^{2}{\theta})-\sin^{2}{\theta}-\sin^{2}{\theta} &= \sin{\theta} \\
1 – 2 \sin^{2}{\theta} &= \sin{\theta} \\
2 \sin^{2}{\theta} + \sin{\theta} – 1 &= 0 \\
(2 \sin{\theta} – 1)(\sin{\theta} + 1) &= 0 \\
\sin{\theta} &= \frac{1}{2}, \, -1
\end{align}
$$

$[2]$
$\displaystyle \sin{\theta} = \frac{1}{2}, \, -1$と$0^{\circ} \leq \theta \leq 360^{\circ}$より$\theta = 30^{\circ}, 150^{\circ}, 270^{\circ}$が得られる。

問題$8 \,$ 円の方程式

中心が$(2,2)$の円の方程式は下記のように表すことができる。
$$
\large
\begin{align}
(x-2)^2 + (y-2)^2 = r^2
\end{align}
$$

ここで上記は$(0,0)$を通るので下記が成立する。
$$
\large
\begin{align}
(0-2)^2 + (0-2)^2 &= r^2 \\
r^2 &= 8
\end{align}
$$

よって、円の方程式は下記のように表せる。
$$
\large
\begin{align}
(x-2)^2 + (y-2)^2 = 8
\end{align}
$$

問題$9 \,$ 二次方程式の複素数解

$x^2-4x+5=0$の複素数解は二次方程式の解の公式を用いることで下記のように得られる。
$$
\large
\begin{align}
x^2 – 4x + 5 &= 0 \\
x &= 2 \pm \sqrt{2^2-5} \\
&= 2 \pm \sqrt{-1} = 2 \pm i
\end{align}
$$

問題$10 \,$ 等差数列の一般項

等差数列$\{ a_n \}$の一般項を$a_n = a_0 + nd$とおく。$a_{1000}=-256, a_{3000}=1024$より下記が成立する。
$$
\large
\begin{align}
a_{1000} &= a_{0} + 1000d = -256 \\
a_{3000} &= a_{0} + 3000d = 1024
\end{align}
$$

上記より$d=0.64, a_0=-896$が得られるので$a_{2000}$は下記のように計算できる。
$$
\large
\begin{align}
a_{2000} &= a_{0} + 2000d \\
&= -896 + 2000 \cdot 0.64 \\
&= 1280 – 896 = 384
\end{align}
$$

問題$11 \,$ 指数法則

下記のように計算できる。
$$
\large
\begin{align}
2^{\frac{1}{6}} \times 4^{\frac{1}{6}} \times 8^{\frac{1}{6}} &= 2^{\frac{1}{6}} \times 2^{\frac{2}{6}} \times 2^{\frac{3}{6}} \\
&= 2^{\frac{1+2+3}{6}} \\
&= 2^1 = 2
\end{align}
$$

問題$12 \,$ 判別式と二次方程式の解

$x^2 – 4kx – k + 5 = 0$の判別式$D$に関して$D<0$が成立すれば良い。
$$
\large
\begin{align}
\frac{D}{4} &= (2k)^{2} – (-k+5) < 0 \\
4k^2 + k – 5 & < 0 \\
(4k+5)(k-1) & < 0
\end{align}
$$

上記より$\displaystyle -\frac{5}{4} < k < 1$が得られる。

問題$13 \,$ 空間ベクトルの成分表示

$\overrightarrow{OA}, \overrightarrow{OB}$はそれぞれ下記のように表すことができる。
$$
\large
\begin{align}
\overrightarrow{OA} &= \left( \begin{array}{c} -1 \\ 4 \\ -2 \end{array} \right) \\
\overrightarrow{OB} &= \left( \begin{array}{c} -3 \\ -3 \\ 1 \end{array} \right)
\end{align}
$$

このとき$\overrightarrow{OB} – \overrightarrow{OA}$は下記のように計算できる。
$$
\large
\begin{align}
\overrightarrow{OB} – \overrightarrow{OA} &= \left( \begin{array}{c} -3 \\ -3 \\ 1 \end{array} \right) – \left( \begin{array}{c} -1 \\ 4 \\ -2 \end{array} \right) \\
&= \left( \begin{array}{c} -2 \\ -7 \\ 3 \end{array} \right)
\end{align}
$$

問題$14 \,$ 多項式関数の定積分

下記のように計算を行うことができる。
$$
\large
\begin{align}
\int_{1}^{2} (6x^2 – 6x + 6) dx &= \left[ 2x^3 – 3x^2 + 6x \right]_{1}^{2} \\
&= (16 – 12 + 12) – (2 – 3 + 6) \\
&= 11
\end{align}
$$

問題$15 \,$ 多項式関数の除算

$2x^3 – 4x + 3$は下記のように表すことができる。
$$
\large
\begin{align}
2x^3 – 4x + 3 = (x+2)(2x^2-4x+4) – 5
\end{align}
$$

上記より商は$2x^2-4x+4$、余りは$-5$である。

$2$次：数理技能検定

問題$1 \,$

問題$2 \,$ 組み合わせと確率

${}_{9} C_{k}$が最大になる$k$が正答率を最小にするので、$k=4, 5$が該当する。

問題$3 \,$ 二項係数とΣの公式

${}_{2} C_{2} + \cdots {}_{n} C_{2}$は下記のように計算できる。
$$
\large
\begin{align}
{}_{2} C_{2} + \cdots {}_{n} C_{2} &= \sum_{k=1}^{n-1} {}_{k+1} C_{2} \\
&= \sum_{k=1}^{n-1} \frac{k(k-1)}{2} \\
&= \frac{1}{2} \sum_{k=1}^{n-1} (k^2 – k) \\
&= \frac{1}{2} \left( \frac{1}{6}(n-1)(n-1+1)(2(n-1)+1) – \frac{1}{2}(n-1)(n-1+1) \right) \\
&= \frac{1}{2} \left( \frac{1}{6}n(n-1)(2n-1) – \frac{1}{2}n(n-1) \right) \\
&= \frac{1}{12} n(n-1)(2n-1-1) \\
&= \frac{1}{6}n(n-1)(n+1)
\end{align}
$$

問題$4 \,$ 三角関数の加法定理

$\sin{2011^{\circ}}$は加法定理などを用いることで下記のように計算できる。
$$
\large
\begin{align}
\sin{2011^{\circ}} &= \sin{(5 \times 360^{\circ} + 211^{\circ})} \\
&= \sin{211^{\circ}} \\
&= \sin{(210^{\circ}+1^{\circ})} \\
&= \sin{210^{\circ}} \cos{1^{\circ}} + \cos{210^{\circ}} \sin{1^{\circ}} \\
&= -\frac{1}{2} \cdot 0.9998 – \frac{\sqrt{3}}{2} \cdot 0.0175 \\
&= -0.515055
\end{align}
$$

・参考
加法定理の公式は下図などを元に抑えておくと良い。

三角関数の加法定理・倍角の公式・極限、微分の公式の簡易的な導出とその直感的理解

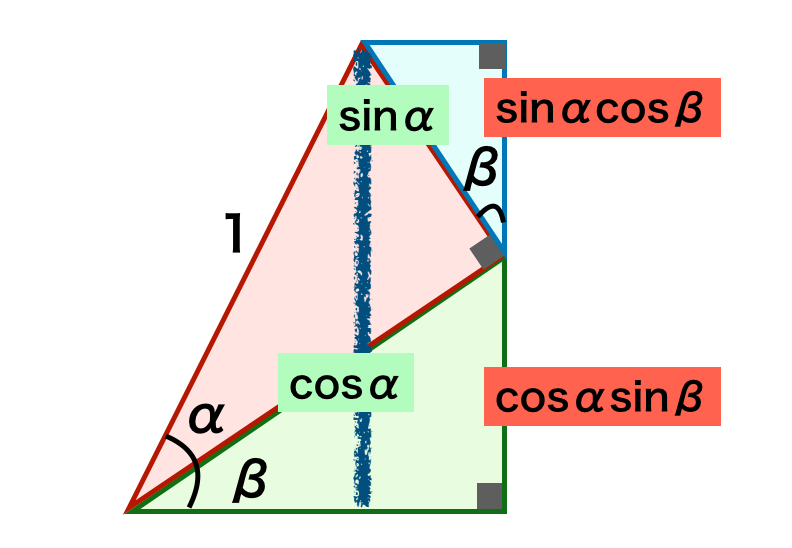
問題$5 \,$ 整数と魔法陣

魔法陣の数字を下記のように$x_1$〜$x_9$を用いて表す。
$$
\large
\begin{align}
\begin{array}{cc} x_1 & x_2 & x_3 \\ x_4 & x_5 & x_6 \\ x_7 & x_8 & x_9 \end{array}
\end{align}
$$

$[1]$
$$
\large
\begin{align}
& x_1 + x_2 + x_3 = x_4 + x_5 + x_6 = x_7 + x_8 + x_9 \\
& x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7 + x_8 + x_9 = 45
\end{align}
$$

上記より、$x_1 + x_2 + x_3 = x_4 + x_5 + x_6 = x_7 + x_8 + x_9 = 15$が得られる。よって魔法陣が成立する場合、数の和は$15$である。

$[2]$
$[1]$より下記が成立する。
$$
\large
\begin{align}
x_1 + x_5 + x_9 = x_3 + x_5 + x_7 = x_2 + x_5 + x_8 = x_4 + x_5 + x_6 = 15
\end{align}
$$

よって下記が得られる。
$$
\large
\begin{align}
(x_1 + x_5 + x_9) + (x_3 + x_5 + x_7) + (x_2 + x_5 + x_8) + (x_4 + x_5 + x_6) &= 60 \\
\sum_{k=1}^{9} x_k + 3x_5 &= 60 \\
45 + 3x_5 &= 60 \\
3x_5 &= 15 \\
x_5 &= 5
\end{align}
$$

上記より$x_5=5$である。

問題$6 \,$ 三角形の相似と$2$次方程式の解の公式・判別式

$[1]$
$BD:AD=AD:CD$が成立するが、$BD, AD, CD$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
BD &= b-x \\
AD &= a \\
CD &= x
\end{align}
$$

よって下記が成立する。
$$
\large
\begin{align}
BD:AD &= AD:CD \\
(b-x):a &= a:x \\
a^2 &= x(b-x) \\
a^2 &= bx – x^2 \\
x^2 – bx + a^2 &= 0
\end{align}
$$

上記より$2$次方程式$x^2 – bx + a^2 = 0$が得られる。

$[2]$
$[1]$で得られた$2$次方程式$x^2 – bx + a^2 = 0$が実数解を持つことから方程式の判別式$D$について$D \geq 0$が成立する。よって下記が成立する。
$$
\large
\begin{align}
D = b^2 – 4 a^2 & \geq 0 \\
b^2 & \geq 4a^2
\end{align}
$$

ここで$a>0, b>0$より$b \geq 2a$が成立する。

$[3]$
$2$次方程式$x^2 – bx + a^2 = 0$は公式より下記のように得られる。
$$
\large
\begin{align}
x = \frac{b \pm \sqrt{b^2-4a^2}}{2}
\end{align}
$$

ここで$BD \geq CD, BD+CD=BC=b$より、$BD$と$CD$はそれぞれ下記のように表すことができる。
$$
\large
\begin{align}
BD &= \frac{b + \sqrt{b^2-4a^2}}{2} \\
CD &= \frac{b – \sqrt{b^2-4a^2}}{2}
\end{align}
$$

問題$7 \,$ 対数関数に基づく関数の最小値・最大値

$[1]$
$1 \leq x \leq 8$のとき$\log_{2}{1} \leq t \leq \log_{2}{8}$であるので$t$の変域は$0 \leq t \leq 3$である。

$[2]$
$y = (\log_{2}{x})^{3} – 3(\log_{2}{x})^{2} + 1$は$t$を用いて下記のように表せる。
$$
\large
\begin{align}
(\log_{2}{x})^{3} – 3(\log_{2}{x})^{2} + 1 = t^3 – 3t^2 + 1
\end{align}
$$

ここで$f(t) = t^3 – 3t^2 + 1$とおくと、$f'(t) = 3t^2-6t = 3t(t-2)$より、$0 \leq t \leq 3$における増減表は下記のようにかける。
$$
\large
\begin{array}{|c|*5{c|}}\hline x & 0 & \cdots & 2 & \cdots & 3 \\
\hline f'(x) & & – & 0 & + & \\
\hline f(x) & 1 & \searrow & -3 & \nearrow & 1 \\
\hline
\end{array}
$$

上記より$\log_{2}{x}=0,3$すなわち$x=1,8$のとき最小値、$\log_{2}{x}=2$すなわち$x=4$のとき最大値をとる。