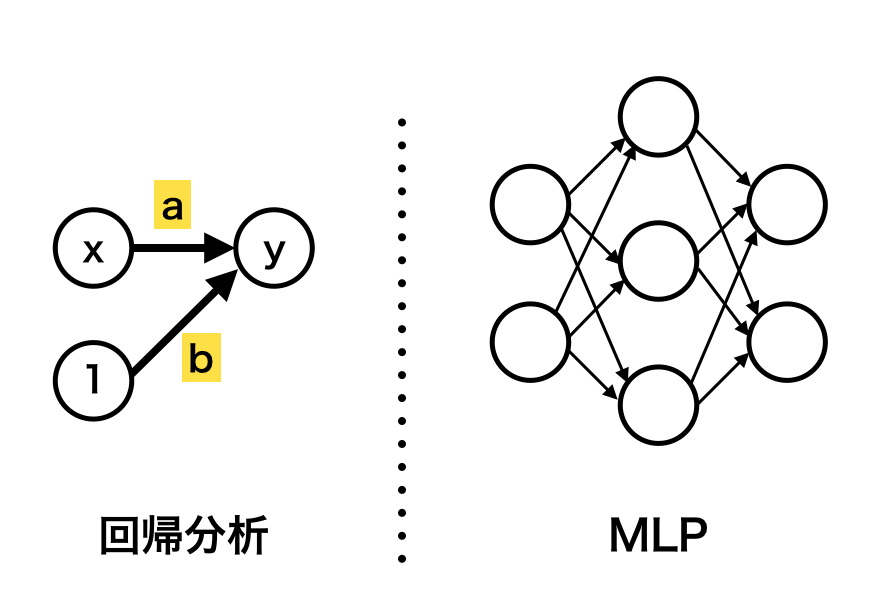
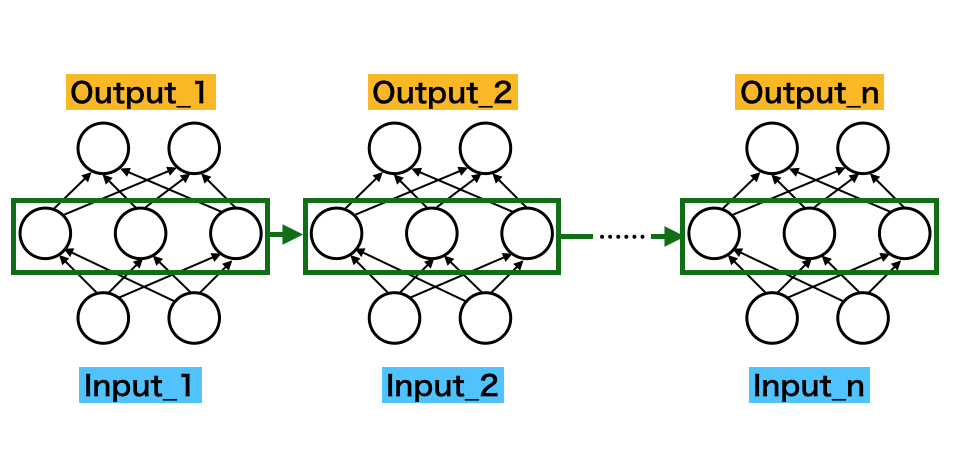
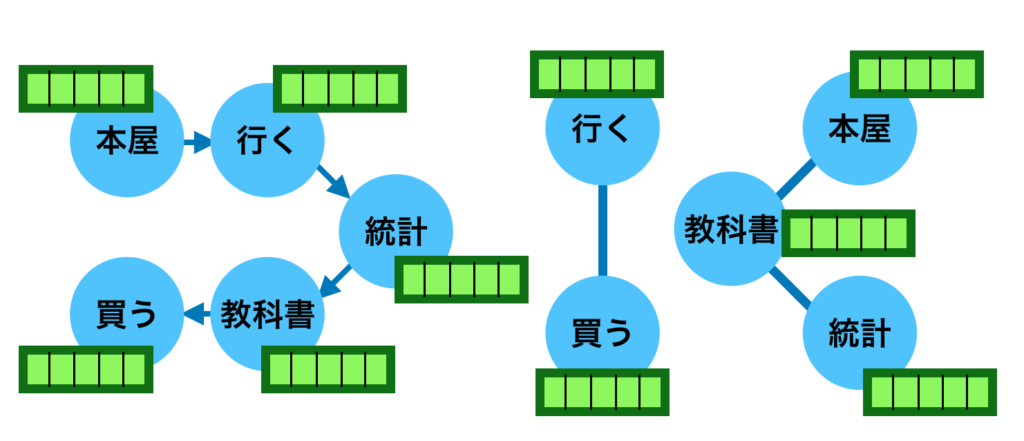
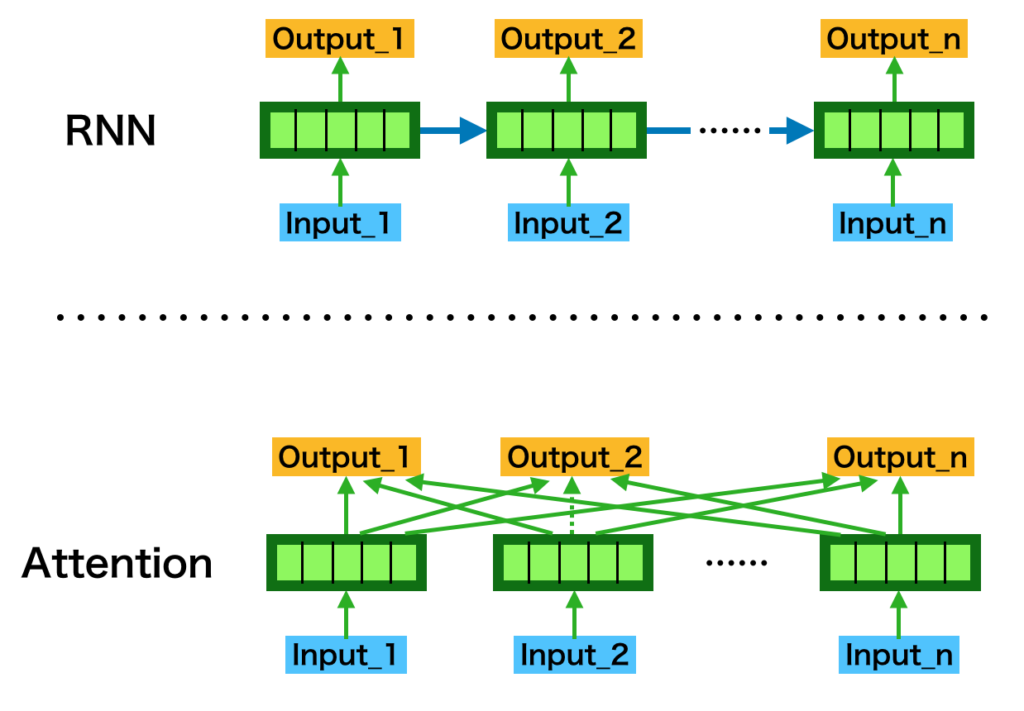
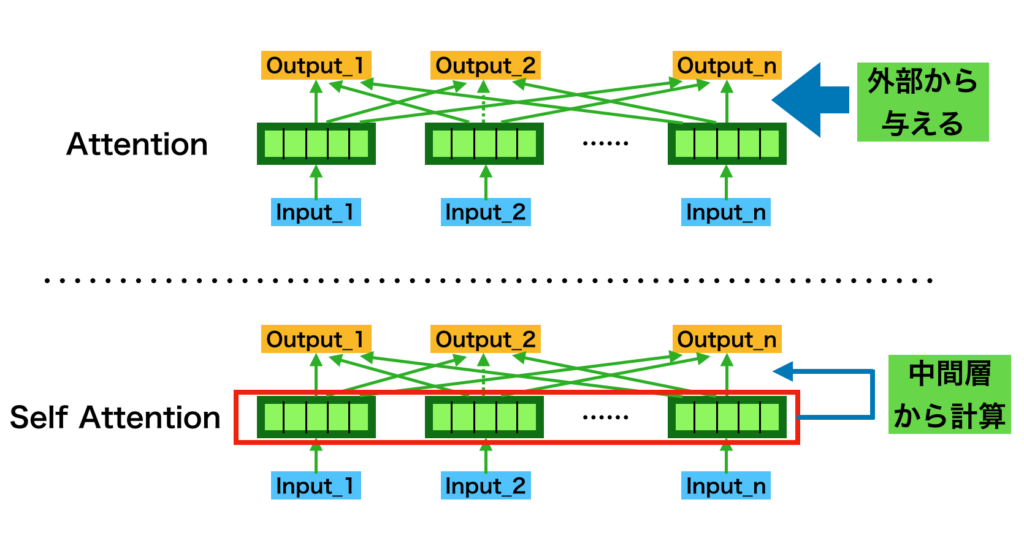
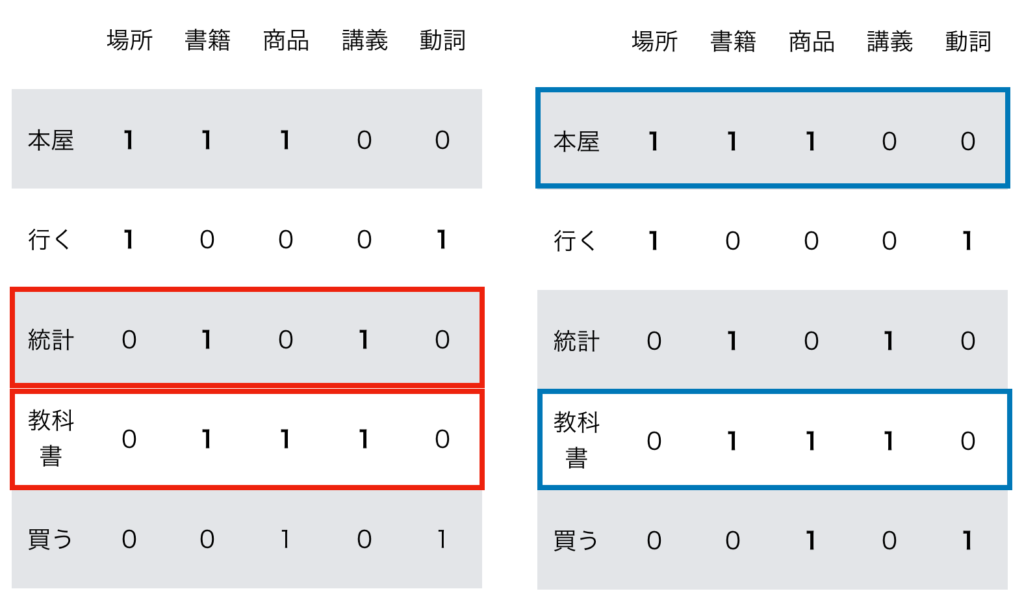
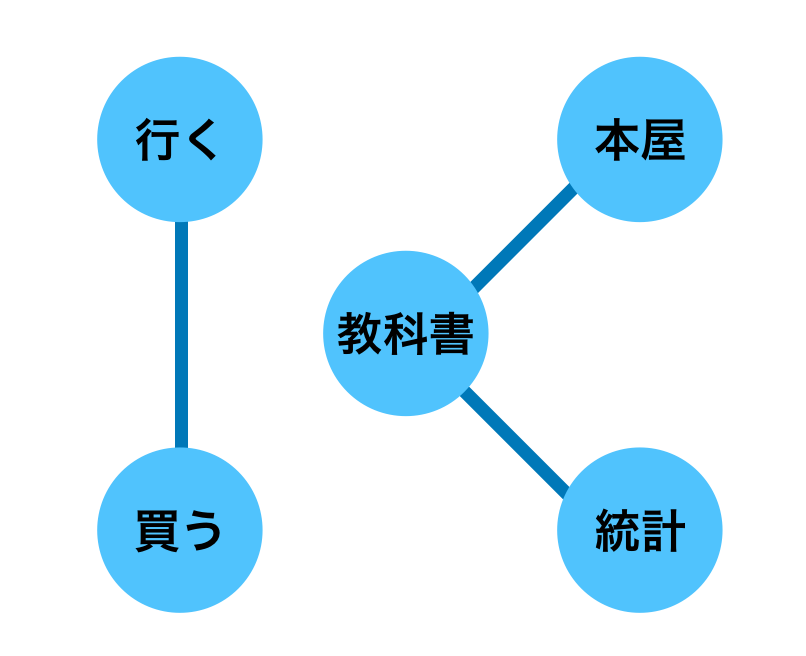
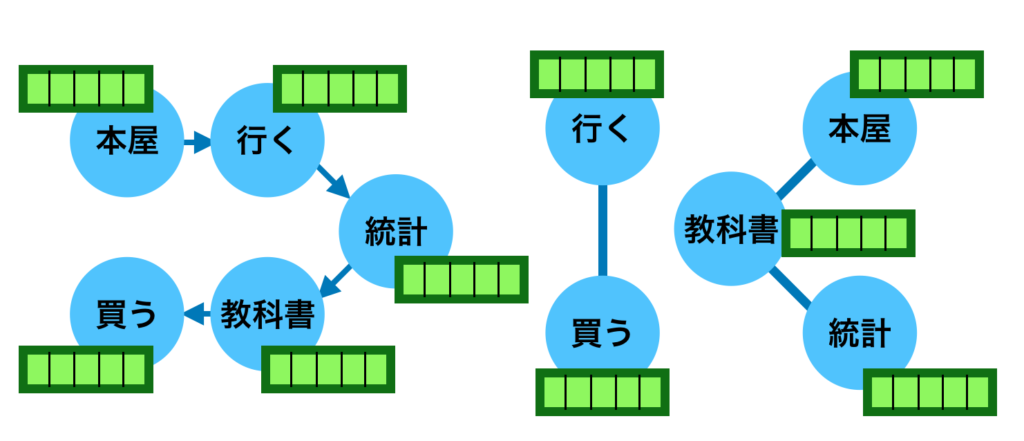
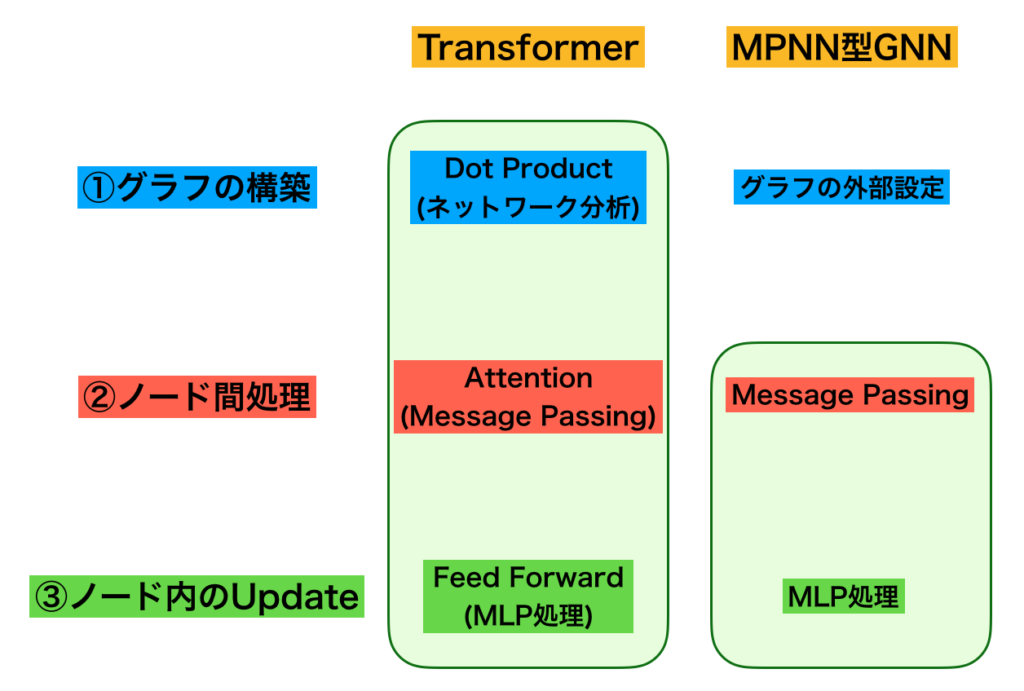
自動微分(Automatic Differentiation)は大規模なニューラルネットワークであるDeepLearningの学習における誤差逆伝播などに用いられる手法です。当記事ではAttention処理とグラフニューラルネットワーク(GNN; Graph Neural Network)の実装について取り扱いました。
作成にあたっては「ゼロから作るDeep Learning②」の第$8$章「Attention」の内容を元に大幅に改変を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
・GNN入門
Contents
MessagePassing
NumPy.repeat
AttentionのようなMessagePassing処理を取り扱う際に係数のベクトルへの掛け算などを行列積で取り扱うのはなかなか難しいので、NumPy.repeatを用いることで要素積の計算を行うというのも一つの手段である。NumPy.repeatはたとえば下記のように使用することができる。
import numpy as np
x1 = np.array([[1., 2., 3.]])
print(x1.shape)
print(x1.repeat(2, axis=0).shape)
print(x1.repeat(2, axis=1).shape)
print(x1.repeat(2, axis=0))
print(x1.repeat(2, axis=1))・実行結果
(1, 3)
(2, 3)
(1, 6)
[[1. 2. 3.]
[1. 2. 3.]]
[[1. 1. 2. 2. 3. 3.]]上記は$2$次元配列の場合であるが、$3$次元の場合も下記のように繰り返し操作を行える。
x2 = np.array([[[1., 2., 3.]]])
print(x2.shape)
print(x2.repeat(2, axis=0).shape)
print(x2.repeat(2, axis=1).shape)
print(x2.repeat(2, axis=2).shape)
print(x2.repeat(2, axis=0))
print(x2.repeat(2, axis=1))
print(x2.repeat(2, axis=2))・実行結果
(1, 1, 3)
(2, 1, 3)
(1, 2, 3)
(1, 1, 6)
[[[1. 2. 3.]]
[[1. 2. 3.]]]
[[[1. 2. 3.]
[1. 2. 3.]]]
[[[1. 1. 2. 2. 3. 3.]]]Attentionの実装
Attentionの基本処理
「ゼロから作るDeepLearning②」ではAttentionの重み付け和の計算にあたって、下記のようなWeightSumクラスを定義する。
class WeightSum:
def __init__(self):
self.params, self.grads = [], []
self.cache = None
def forward(self, hs, a):
N, T, H = hs.shape
ar = a.reshape(N, T, 1).repeat(H, axis=2)
t = hs * ar
c = np.sum(t, axis=1)
self.cache = (hs, ar)
return c
def backward(self, dc):
hs, ar = self.cache
N, T, H = hs.shape
dt = dc.reshape(N, 1, H).repeat(T, axis=1)
dar = dt * hs
dhs = dt * ar
da = np.sum(dar, axis=2)
return dhs, da順伝播の実行例
a = np.array([[1., 0.5], [0.2, 0.5]])
hs = np.ones([2, 2, 3])
calc_weight_sum = WeightSum()
c = calc_weight_sum.forward(hs, a)
print(c)・実行結果
[[1.5 1.5 1.5]
[0.7 0.7 0.7]]逆伝播の実行例
dc = np.ones([2, 3])
dhs, da = calc_weight_sum.backward(dc)
print(dhs.shape)
print(dhs)
print("===")
print(da.shape)
print(da)・実行結果
(2, 2, 3)
[[[1. 1. 1. ]
[0.5 0.5 0.5]]
[[0.2 0.2 0.2]
[0.5 0.5 0.5]]]
===
(2, 2)
[[3. 3.]
[3. 3.]]MessagePassingの実装
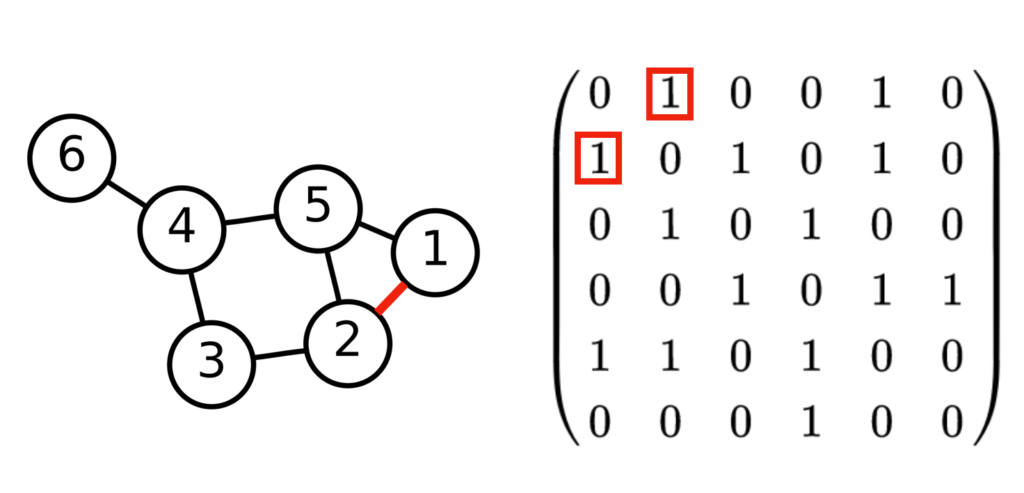
隣接行列:グラフの定義
$5$ノードのグラフの隣接行列は下記のように定義することができる。
adj_mat = np.array([[1, 0, 1, 1, 0], [0, 1, 1, 0, 1], [1, 1, 1, 0, 1], [1, 0, 0, 1, 1], [0, 1, 1, 1, 1]])
print(adj_mat)
print(adj_mat==adj_mat.T)・実行結果
[[1 0 1 1 0]
[0 1 1 0 1]
[1 1 1 0 1]
[1 0 0 1 1]
[0 1 1 1 1]]
[[ True True True True True]
[ True True True True True]
[ True True True True True]
[ True True True True True]
[ True True True True True]]ここでは無向グラフを取り扱うので、隣接行列が対称行列であることも合わせて確認しておくと良い。
MessagePassingクラスの実装
WeightSumクラスを改変することで下記のようにMessagePassingクラスの実装を行なった。
class MessagePassing:
def __init__(self, adj_mat):
self.params, self.grads = [], []
self.graph = adj_mat
self.cache = None
def forward(self, h):
N, T, H = h.shape
m_t = np.zeros_like(h)
for i in range(self.graph.shape[0]):
ar = self.graph[i,:].reshape(1, T, 1).repeat(N, axis=0).repeat(H, axis=2)
t = h * ar
m_t[:, i, :] = np.sum(t, axis=1)
self.cache = h
return m_t
def backward(self, dc):
h = self.cache
N, T, H = h.shape
dh = np.zeros_like(h)
for i in range(self.graph.shape[0]):
ar = self.graph[i, :].reshape(1, T, 1).repeat(N, axis=0).repeat(H, axis=2)
dt = dc.reshape(N, 1, H).repeat(T, axis=1)
dh[:, i, :] = np.sum(dt * ar, axis=1)
return dh上記のMessagePassingクラスではWeightSumクラスの重み付け和の計算にあたって、隣接行列を用いるように改変を行なった。
MessagePassingクラスの実行例
■ 順伝播
順伝播の計算は下記のように実行することができる。
calc_mp = MessagePassing(adj_mat)
h = np.ones([2, 5, 3])
h[0,0,0] = 5
m_t = calc_mp.forward(h)
print(m_t.shape)
print(m_t)・実行結果
(2, 5, 3)
[[[7. 3. 3.]
[3. 3. 3.]
[8. 4. 4.]
[7. 3. 3.]
[4. 4. 4.]]
[[3. 3. 3.]
[3. 3. 3.]
[4. 4. 4.]
[3. 3. 3.]
[4. 4. 4.]]]上記の結果が正しいかどうかは、下記のような計算を行うことで確認できる。
print(np.sum(h[0, :, 0] * adj_mat[0, :]))
print(np.sum(h[0, :, 0] * adj_mat[2, :]))
print(np.sum(h[0, :, 0] * adj_mat[3, :]))・実行結果
7.0
8.0
7.0■ 逆伝播
dc = np.ones([2, 3])
dh = calc_mp.backward(dc)
print(dh)・実行結果
[[[3. 3. 3.]
[3. 3. 3.]
[4. 4. 4.]
[3. 3. 3.]
[4. 4. 4.]]
[[3. 3. 3.]
[3. 3. 3.]
[4. 4. 4.]
[3. 3. 3.]
[4. 4. 4.]]]GNNの実装
GNNのレイヤーの実装
クラスの実装
■ Affineクラス
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx■ GNN_Layerクラス
class GNN_Layer:
def __init__(self, W, b, adj_mat):
self.W = W
self.b = b
self.dW = np.zeros_like(W)
self.db = np.zeros_like(b)
self.h = None
self.graph = adj_mat
def forward(self, h):
N, T, H = h.shape
self.h = h
self.affines = []
self.calc_mp = MessagePassing(self.graph)
m_t = self.calc_mp.forward(h)
h_next = np.zeros_like(h)
for i in range(self.graph.shape[0]):
affine = Affine(self.W, self.b)
h_next[:, i, :] = affine.forward(m_t[:, i, :])
self.affines.append(affine)
return h_next
def backward(self, dh_next):
N, T, H = self.h.shape
dh = np.zeros_like(self.h)
for i in range(self.graph.shape[0]):
dh[:, i, :] = self.affines[i].backward(dh_next[:, i, :])
self.dW += self.affines[i].dW
self.db += self.affines[i].db
dh = self.calc_mp.backward(dh)
return dh使用例
■ 順伝播
N, T, H = 2, 5, 3
h = np.ones([2, 5, 3])
W = np.ones([H, H])
b = np.ones(H)
adj_mat = np.array([[1, 0, 1, 1, 0], [0, 1, 1, 0, 1], [1, 1, 1, 0, 1], [1, 0, 0, 1, 1], [0, 1, 1, 1, 1]])
gnn_layer = GNN_Layer(W, b, adj_mat)
h_next = gnn_layer.forward(h)
print(h_next)・実行例
[[[10. 10. 10.]
[10. 10. 10.]
[13. 13. 13.]
[10. 10. 10.]
[13. 13. 13.]]
[[10. 10. 10.]
[10. 10. 10.]
[13. 13. 13.]
[10. 10. 10.]
[13. 13. 13.]]]■ 逆伝播
dh_next = np.ones([2, 5, 3])
dh = gnn_layer.backward(dh_next)
print(dh)・実行結果
[[[ 9. 9. 9.]
[ 9. 9. 9.]
[12. 12. 12.]
[ 9. 9. 9.]
[12. 12. 12.]]
[[ 9. 9. 9.]
[ 9. 9. 9.]
[12. 12. 12.]
[ 9. 9. 9.]
[12. 12. 12.]]]$2$層GNNの実装
関数・クラスの実装
■ 活性化関数・誤差関数
def softmax(a): # a is 2D-Array
c = np.max(a, axis=1)
exp_a = np.exp(a.T-c)
sum_exp_a = np.sum(exp_a, axis=0)
y = (exp_a / sum_exp_a).T
return y
def softmax_3D(a): # a is 3D-Array
N, L, H = a.shape
c = np.max(a, axis=2)
exp_a = np.exp(a-c.reshape([N, L, 1]).repeat(H, axis=2))
sum_exp_a = np.sum(exp_a, axis=2)
y = exp_a / sum_exp_a.reshape([N, L, 1]).repeat(H, axis=2)
return y
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum(t * np.log(y+delta))
class Softmax:
def __init__(self):
self.loss = None
self.y = None
def forward(self, x):
self.y = softmax_3D(x)
return self.y
def backward(self, dout):
dx = dout * self.y * (1-self.y)
return dx
class Aggregate:
def __init__(self):
self.h = None
self.y = None
def forward(self, h):
self.h = h
self.y = np.sum(h, axis=1)
return self.y
def backward(self, dy):
N, T, H = self.h.shape
dh = dy.reshape(N, 1, H).repeat(T, axis=1)
return dh
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1.):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
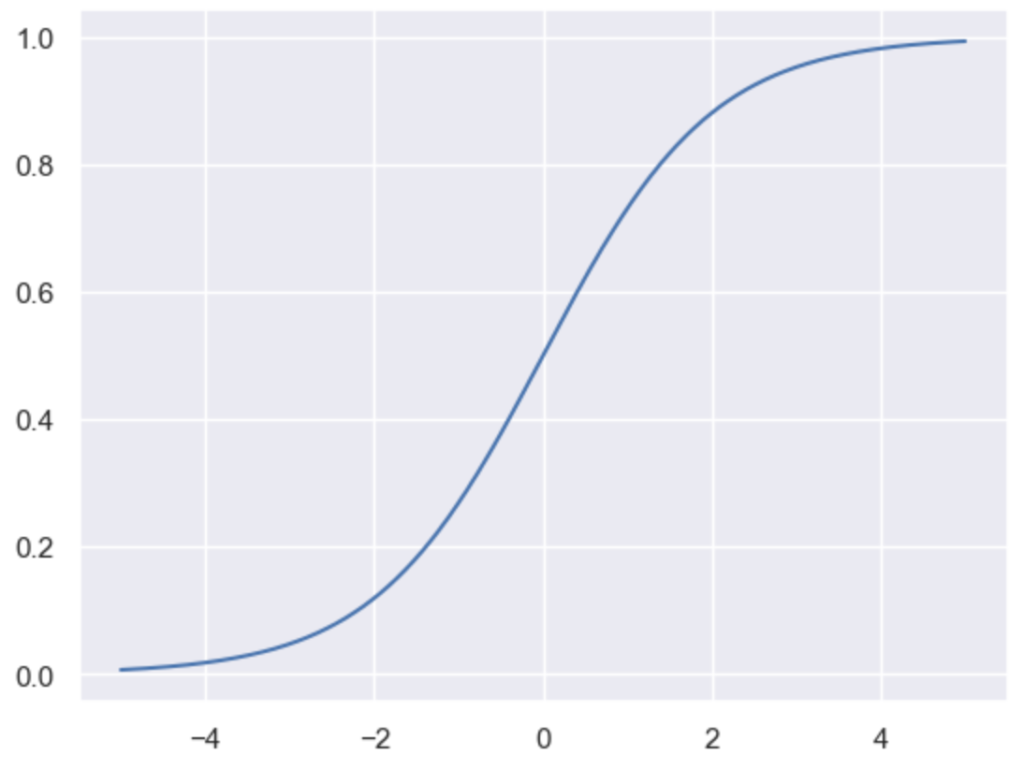
return dx途中で用いたソフトマックス関数は下記のように定義される。
$$
\large
\begin{align}
y_k &= \mathrm{Softmax}(x_k) = \frac{\exp{(x_k)}}{S} \\
S &= \sum_{j} \exp{(x_j)}
\end{align}
$$
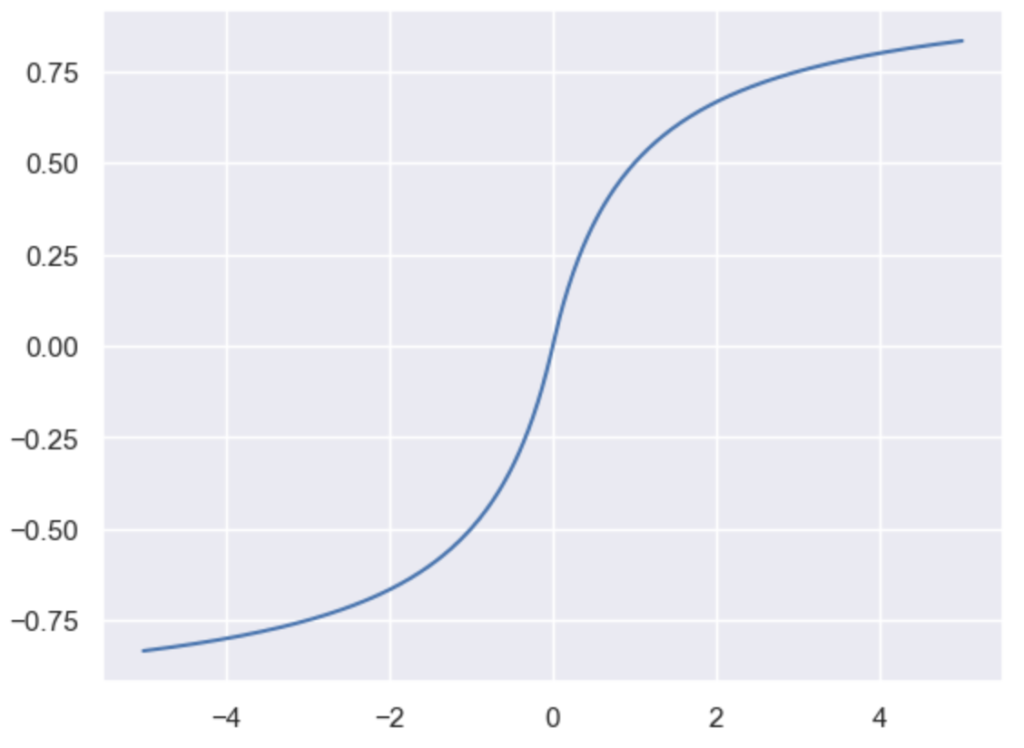
上記の$x_k$に関する偏微分は分数関数の微分の公式を元に下記のように計算できる。
$$
\large
\begin{align}
\frac{\partial y_k}{\partial x_k} &= \frac{\exp{(x_k)}S – \exp{(x_k)} \cdot \exp{(x_k)}}{S^{2}} \\
&= \frac{\exp{(x_k)}(S – \exp{(x_k)})}{S^{2}} \\
&= \frac{\exp{(x_k)}}{S} \cdot \left( 1 – \frac{\exp{(x_k)}}{S} \right) = y_k(1-y_k)
\end{align}
$$
上記に基づいてSoftmaxクラスのbackwardメソッドの実装を行なった。
■ $2$層GNN
from collections import OrderedDict
class TwoLayerGNN:
def __init__(self, input_size, hidden_size, output_size, adj_mat, weight_init_std=0.01):
self.params = {}
self.params["W1"] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params["b1"] = np.zeros(hidden_size)
self.params["W2"] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params["b2"] = np.zeros(output_size)
# generate layers
self.layers = OrderedDict()
self.layers["GNN_layer1"] = GNN_Layer(self.params["W1"], self.params["b1"], adj_mat)
self.layers["Softmax1"] = Softmax()
self.layers["GNN_layer2"] = GNN_Layer(self.params["W2"], self.params["b2"], adj_mat)
self.layers["Aggregate"] = Aggregate()
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def calc_gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = self.lastLayer.backward(1.)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# output
grads = {}
grads["W1"] = self.layers["GNN_layer1"].dW
grads["b1"] = self.layers["GNN_layer1"].db
grads["W2"] = self.layers["GNN_layer2"].dW
grads["b2"] = self.layers["GNN_layer2"].db
return grads実行例
■ softmax_3D関数
x = np.ones([2,5,3])
x[:, :, 1] = 2
softmax_3D(x)・実行結果
array([[[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156]],
[[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156],
[0.21194156, 0.57611688, 0.21194156]]])■ 学習の実行
np.random.seed(0)
alpha = 0.1
adj_mat = np.array([[1, 0, 1, 1, 0], [0, 1, 1, 0, 1], [1, 1, 1, 0, 1], [1, 0, 0, 1, 1], [0, 1, 1, 1, 1]])
x = np.ones([2, 5, 2])
x[0, :, :1] = -1.
t = np.array([[1., 0.], [0., 1.]])
network = TwoLayerGNN(2, 2, 2, adj_mat)
for i in range(10):
grad = network.calc_gradient(x, t)
for key in ("W1", "b1", "W2", "b2"):
network.params[key] -= alpha * grad[key]
if (i+1)%2==0:
print(softmax(network.predict(x)))・実行結果
[[9.99882931e-01 1.17068837e-04]
[9.99882862e-01 1.17138203e-04]]
[[2.09556970e-08 9.99999979e-01]
[3.65517109e-09 9.99999996e-01]]
[[9.99966650e-01 3.33497863e-05]
[1.24346800e-12 1.00000000e+00]]
[[1.00000000e+00 1.81375702e-28]
[1.59424189e-14 1.00000000e+00]]
[[1.00000000e+00 1.22993158e-51]
[1.62446544e-16 1.00000000e+00]]■ 推論
x = np.array([[[-1, 1], [-1, 1], [-0.5, 0.3], [-1.2, 0.8], [-0.9, 1.]]])
print(network.predict(x))
print(softmax(network.predict(x)))・実行結果
[[ 58.68030203 -58.54451771]]
[[1.00000000e+00 1.23000717e-51]]