ブログ

Contents

1 演習問題解答例

演習問題解答例

12-1. 相関分析

① 以下の通り

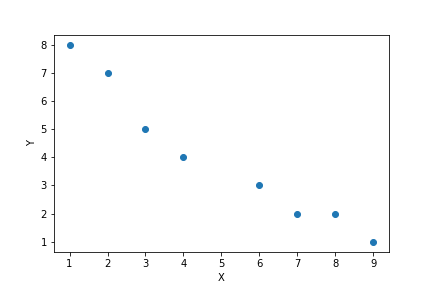
② 相関係数$r$は$2$変数$x, y$の間にどの程度の直線的な関連があるかを表す指標である。$x, y$のデータが標本の場合、相関係数(厳密には標本相関係数)は以下の式で表される。
$-1 \leq r \leq 1$の範囲で値をとり、$-1$または$1$に近いほど強い相関があるといえる。

$$
\begin{align*}
r_{xy}
&= \frac{s_{xy}}{s_x s_y}\\
&= \frac{\sum_{i = 1}^n (x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum_{i = 1}^n (x_i – \bar{x})^2}\sqrt{\sum_{i = 1}^n (y_i – \bar{y})^2}}\\
&= \frac{n \cdot \sum_{i=1}^n (xy) – (\sum_{i=1}^n x)\cdot (\sum_{i=1}^n y)}{\sqrt{(n \cdot \sum_{i=1}^n x^2 – (\sum_{i=1}^n x)^2) \cdot (n\cdot \sum_{i=1}^n y^2 – (\sum_{i=1}^n y)^2)}}\\
\end{align*}
$$

$r_{xy}$: $x$と$y$の相関係数
$\bar{x}$: $x$の平均
$\bar{y}$: $y$の平均
$s_{xy}$: $x$と$y$の共分散
$s_x$: $x$の標準偏差
$s_y$: $y$の標準偏差

$\bar{x} = 5, \bar{y} = 4$であり、

$$
\begin{align*}
\sum_{i = 1}^n (x_i – \bar{x})(y_i – \bar{y}) &= -50\\
\sum_{i = 1}^n (x_i – \bar{x})^2 &=60\\
\sum_{i = 1}^n (y_i – \bar{y})^2 &=44
\end{align*}
$$

である。

よって、$\displaystyle r_{xy}=\frac{-50}{\sqrt{60}\cdot\sqrt{44}}=-0.973$

③ 問のデータ表から以下の通り計算できる。

$$
\begin{align*}
&\sum_{i=1}^n (xy)=110\\
&\sum_{i=1}^n x = 40\\
&\sum_{i=1}^n y = 32\\
&\sum_{i=1}^n x^2 = 260\\
&\sum_{i=1}^n y^2 = 172\\
& \left(\sum_{i=1}^n x \right)^2 = 1600\\
& \left(\sum_{i=1}^n y \right)^2 = 1024
\end{align*}
$$

よって、

$$
\begin{align*}
r_{xy} &=\frac{(8 \cdot 110-40\cdot32)}{\sqrt{(8\cdot 260-1600) \cdot (8 \cdot 172-1024)}}\\
&=\frac{-400}{\sqrt{(480) \cdot (352)}}\\
&=\frac{-400}{\sqrt{168960}}\\
&=-0.973
\end{align*}
$$

④ 上記で求めた標本相関係数から、母集団の相関係数$\rho$が$0$であるかを検定する方法を無相関検定という。計算した標本相関係数$r$の絶対値が$204$ページの表$12$-$4$に示された数値(臨界値)より大きければ、母集団における$2$つの変数間に有意な相関があり($\rho\neq0$)、逆に臨界値より小さければ有意な相関があるとは言えない。

帰無仮説:母集団における$2$つの変数間の相関係数は$0$である。($\rho=0$)
対立仮説:母集団における$2$つの変数間に相関がある。($\rho\neq0$)

標本サイズ$n=8$より、自由度は$n-2=6$であり、自由度$6$、有意水準$5％$で両側検定を行う。自由度$6$の両側検定における有意水準$5％$点の臨界点は、表より$0.707$であり、これは上記で求めた相関係数$r_{xy}$の絶対値の方が大きいため、帰無仮説は棄却される。よって母集団の$2$つの変数間には相関があると言える。

12-2. 相関分析

① 下図の通り。

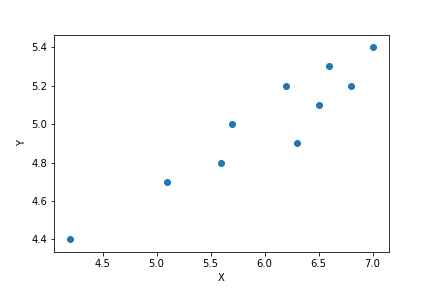
② 問のデータ表から、

$\bar{x} = 5$、$\bar{y} = 4$であり、

$$
\begin{align*}
&\sum_{i = 1}^n (x_i – \bar{x})(y_i – \bar{y})=2.23\\
&\sum_{i = 1}^n (x_i – \bar{x})^2=6.68\\
&\sum_{i = 1}^n (y_i – \bar{y})^2=0.84
\end{align*}
$$

よって、

$$r_{xy}=\frac{2.23}{\sqrt{6.68}\cdot\sqrt{0.84}}=0.9414$$

③ 問のデータ表から、

$$
\begin{align*}
&\sum_{i=1}^n (xy)=302.23\\
&\sum_{i=1}^n x = 60\\
&\sum_{i=1}^n y = 50\\
&\sum_{i=1}^n x^2 = 366.68\\
&\sum_{i=1}^n y^2 = 250.84\\
&\left(\sum_{i=1}^n x\right)^2 = 3600\\
&\left(\sum_{i=1}^n y \right)^2 = 2500
\end{align*}
$$

よって、

$$
\begin{align*}
r_{xy} &= \frac{(10 \cdot 302.23-60\cdot50)}{\sqrt{(10\cdot 366.68-3600) \cdot (10 \cdot 250.84-2500)}}\\
&= \frac{22.3}{\sqrt{(66.8) \cdot (8.4)}}\\
&= \frac{22.3}{\sqrt{561.12}}\\
&= 0.9414
\end{align*}
$$

④ 帰無仮説、対立仮説は以下の通り。

帰無仮説:母集団における2つの変数間の相関係数は$0$である。($\rho=0$)
対立仮説:母集団における2つの変数間に相関がある($\rho\neq0$)

標本サイズ$n=10$より、自由度は$n-2=8$であり、自由度$8$、有意水準$5％$で両側検定を行う。自由度$6$の両側検定における有意水準$5％$点の臨界点は、表より$0.632$であり、これは上記で求めた相関係数$r_{xy}$の絶対値の方が大きいため、帰無仮説は棄却される。よって母集団の$2$つの変数間には相関があると言える。

12-3. 相関分析

① 下図の通り。

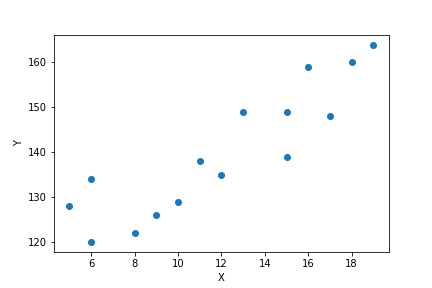
② 問のデータ表から、$\bar{x} = 12$、$\bar{y} = 140$であり、

$$
\begin{align*}
\sum_{i = 1}^n (x_i – \bar{x})(y_i – \bar{y})=815\\
\sum_{i = 1}^n (x_i – \bar{x})^2=296\\
\sum_{i = 1}^n (y_i – \bar{y})^2=2814
\end{align*}
$$

よって、

$$r_{xy}=\frac{815}{\sqrt{296}\cdot\sqrt{2814}}=0.8930$$

となる。

③ 問のデータ表から、

$$
\begin{align*}
&\sum_{i=1}^n (xy)=26015\\
&\sum_{i=1}^n x = 180\\
&\sum_{i=1}^n y = 2100\\
&\sum_{i=1}^n x^2 = 2456\\
&\sum_{i=1}^n y^2 = 296814\\
&\left(\sum_{i=1}^n x \right)^2 = 32400\\
&\left(\sum_{i=1}^n y \right)^2 = 4410000
\end{align*}
$$

よって、

$$
\begin{align*}
r_{xy} &= \frac{(15 \cdot 26015-180\cdot2100)}{\sqrt{(15\cdot 2456-32400) \cdot (15 \cdot 296814-4410000)}}\\
&= \frac{12225}{\sqrt{(4400) \cdot (42210)}}\\
&= \frac{12225}{\sqrt{187412400}}\\
&= 0.8930
\end{align*}
$$

となる。

④ 帰無仮説、対立仮説は以下の通り。

帰無仮説:母集団における$2$つの変数間の相関係数は$0$である。($\rho=0$)
対立仮説:母集団における$2$つの変数間に相関がある。($\rho\neq0$)

標本サイズ$n=15$より、自由度は$n-2=13$であり、自由度$13$、有意水準$5％$および有意水準$1％$で両側検定を行う。

自由度$13$の両側検定における有意水準$5％$点の臨界点は、表より$0.514$であり、これは上記で求めた相関係数$r_{xy}$の絶対値の方が大きいため、帰無仮説は棄却される。よって母集団の２つの変数間には相関があると言える。

また、自由度$13$の両側検定における有意水準$1％$点の臨界点は、表より$0.641$であり、これは上記で求めた相関係数$r_{xy}$の絶対値の方が大きいため、帰無仮説は棄却される。よって母集団の２つの変数間には相関があると言える。

12-4. 相関分析: 相関行列の作成

① 定義通り計算すると以下の通りとなる。

(1)平均

英語: $70$
国語: $75$
数学: $54$
社会: $66$
理科: $60$

(2)分散

英語: $100$
国語: $64$
数学: $289$
社会: $144$
理科: $225$

(3)標準偏差

英語: $10$
国語: $8$
数学: $17$
社会: $12$
理科: $15$

② ③ 定義通り算出することで下記の表が得られる

12-5. スピアマンの順位和相関係数

スピアマンの順位和相関係数$r_s$は$2$組のデータ$X, Y$が数量ではなく、順位で与えられているときに$X$と$Y$の間の相関関係の強さを調べるための指標である。スピアマンの順位和相関係数のとりうる値の範囲及び解釈は通常の相関係数と同様である。通常の相関係数より、外れ値の影響を受けにくいというメリットがある。

$$
r_s = 1-\frac{6 \sum_{i = 1}^n{(X-Y)^2}}{n(n^2-1)}
$$

① 下記のように順位をもとに$X-Y$及び$(X-Y)^2$を計算する。同順位のデータがある場合はデータを加工する。この場合は$X$が$6$位の値が$2$つあるため、6.5に変更する。

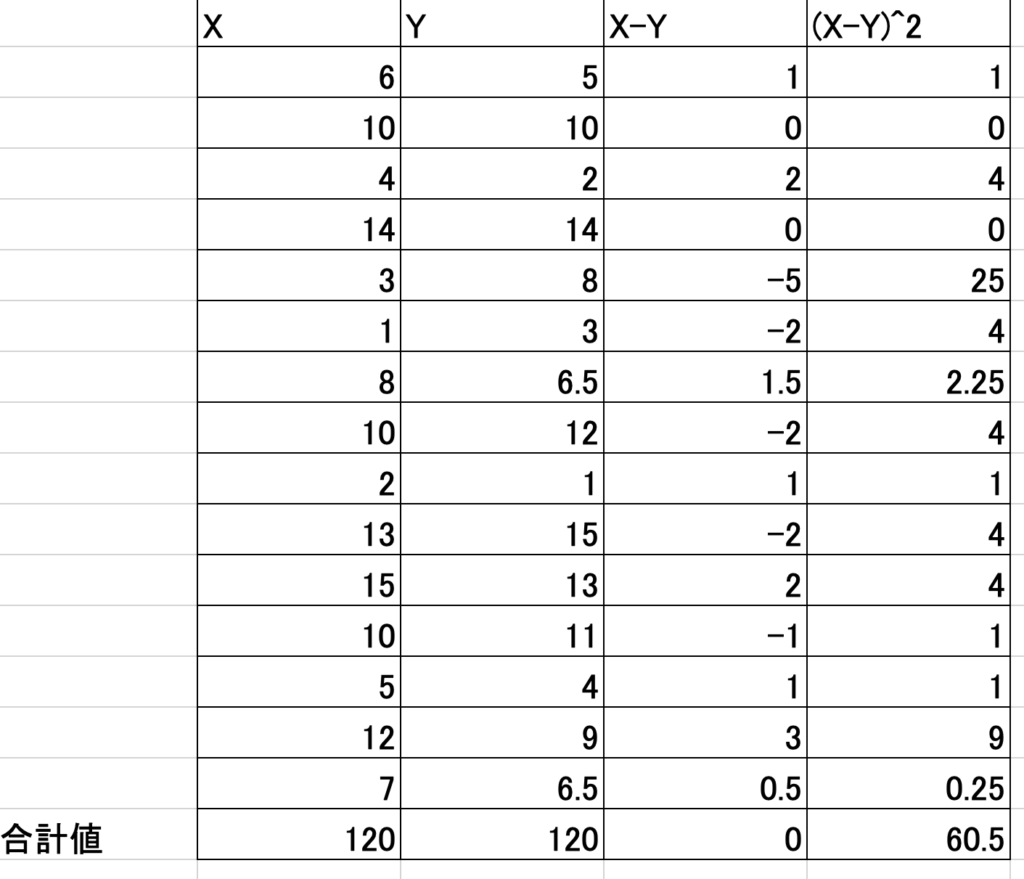
上記の計算結果をもとにスピアマンの順位和相関係数$r_s$を計算する。

$$
\begin{align*}
r_s &= 1-\frac{6 \sum_{i = 1}^n{(X-Y)^2}}{n(n^2-1)}\\
&=1-\frac{6 \cdot 60.5}{15(15^2-1)}\\
&=1-\frac{363}{3360}\\
&=0.892\\
\end{align*}
$$

② 相関係数と同様に書籍$p. 208$の表$12$-$6$を用いればスピアマンの順位和相関係数も検定を行うことができる。

帰無仮説:母集団における2つの変数間に有意な相関があるとは言えない($\rho=0$)
対立仮説:母集団における2つの変数間に有意な相関があると言える($\rho\neq0$)

標本サイズ$n=15$より、標本サイズ$15$、有意水準$10％$、有意水準$5％$および有意水準$1％$で両側検定を行う。標本サイズ$15$の両側検定における有意水準$10％$点の臨界点は、表より$0.446$であり、これは上記で求めた相関係数$r_{xy}$の絶対値の方が大きいため、帰無仮説は棄却される。よって母集団の２つの変数間には相関があると言える。

標本サイズ$15$の両側検定における有意水準$5％$点の臨界点は、表より$0.521$であり、これは上記で求めた相関係数$r_{xy}$の絶対値の方が大きいため、帰無仮説は棄却される。よって母集団の２つの変数間には相関があると言える。

標本サイズ$15$の両側検定における有意水準$1％$点の臨界点は、表より$0.657$であり、これは上記で求めた相関係数$r_{xy}$の絶対値の方が大きいため、帰無仮説は棄却される。よって母集団の２つの変数間には相関があると言える。

Ch.14 「ベクトルと行列の加減」の演習問題の解答例　〜統計学のための数学入門30講〜

投稿日: 2022-12-142022-12-30 投稿者: lib-arts

当記事は「統計学のための数学入門$30$講(朝倉書店)」の読解サポートにあたってChapter.$14$の「ベクトルと行列の加減」の章末問題の解答の作成を行いました。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

・書籍解答まとめ
https://www.hello-statisticians.com/answer_textbook_math#math_stat

統計学のための数学入門30講 (科学のことばとしての数学)

Contents

1 本章のまとめ
2 演習問題解答
- 2.1 問題$14.1$
- 2.2 問題$14.2$

本章のまとめ

演習問題解答

問題$14.1$

$$
\large
\begin{align}
A = \left(\begin{array}{ccc} 1 & 2 & 4 \\ 3 & 6 & 7 \\ 5 & 8 & 9 \end{array} \right), \quad B = \left(\begin{array}{ccc} 1 & 0.3 & 0.5 \\ 0.3 & 1 & 0.7 \\ 0.5 & 0.7 & 1 \end{array} \right), \quad C = \left(\begin{array}{cccc} 2 & 3 & 5 & 4 \\ 1 & 2 & 6 & 8 \\ 7 & 1 & 9 & 7 \end{array} \right)
\end{align}
$$

$A, B$は$3 \times 3$正方行列、$C$は$3 \times 4$行列である。また、それぞれの転置行列は下記のように表せる。
$$
\large
\begin{align}
A^{\mathrm{T}} &= \left(\begin{array}{ccc} 1 & 3 & 5 \\ 2 & 6 & 8 \\ 4 & 7 & 9 \end{array} \right) \\
B^{\mathrm{T}} &= \left(\begin{array}{ccc} 1 & 0.3 & 0.5 \\ 0.3 & 1 & 0.7 \\ 0.5 & 0.7 & 1 \end{array} \right) \\
C^{\mathrm{T}} &= \left(\begin{array}{ccc} 2 & 1 & 7 \\ 3 & 2 & 1 \\ 5 & 6 & 9 \\ 4 & 8 & 7 \end{array} \right)
\end{align}
$$

問題$14.2$

$2A+3B$は下記のように計算できる。
$$
\large
\begin{align}
2A+3B &= 2 \left(\begin{array}{ccc} 1 & 2 & 4 \\ 3 & 6 & 7 \\ 5 & 8 & 9 \end{array} \right) + 3 \left(\begin{array}{ccc} 1 & 0.3 & 0.5 \\ 0.3 & 1 & 0.7 \\ 0.5 & 0.7 & 1 \end{array} \right) \\
&= \left(\begin{array}{ccc} 5 & 4.9 & 9.5 \\ 6.9 & 15 & 16.1 \\ 11.5 & 18.1 & 21 \end{array} \right)
\end{align}
$$

$\mathrm{Tr}(2A+3B), 2\mathrm{Tr}(A)+3\mathrm{Tr}(B)$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
\mathrm{Tr}(2A+3B) &= 5 + 15 + 21 = 41 \\
2\mathrm{Tr}(A)+3\mathrm{Tr}(B) &= 2(1+6+9) + 3(1+1+1) = 41
\end{align}
$$

よって$\mathrm{Tr}(2A+3B) = 2\mathrm{Tr}(A)+3\mathrm{Tr}(B)$が成立することが確認できる。

Ch.8 「推定量とその性質」の章末問題の解答例　〜数理統計学(共立出版)〜

投稿日: 2022-12-132022-12-02 投稿者: lib-arts

当記事は「数理統計学(共立出版)」の読解サポートにあたってChapter.$8$の「推定量とその性質」の章末問題の解答の作成を行いました。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

・解答まとめ
https://www.hello-statisticians.com/answer_textbook_math_stat#green

数理統計学: 統計的推論の基礎

黒木学

3,190円(11/06 08:31時点)

Contents

1 章末の演習問題について
2 まとめ

章末の演習問題について

問題8.1の解答例

有効推定量を直接計算することはできないので、以下、$\beta$の最尤推定量を計算し、最尤推定量が有効推定量であることを示す。確率変数$X_i \sim \mathrm{Ex}(1/\beta) = \mathrm{Ga}(1,\beta)$より、確率密度関数を$f(x)$とおくと下記のように表せる。
$$
\large
\begin{align}
f(x) = \frac{1}{\beta} e^{-\frac{x}{\beta}}
\end{align}
$$

上記から得られる標本の実現値を$x_1, …, x_n$とするとき、尤度関数$L(\beta)$は下記のように表せる。
$$
\large
\begin{align}
L(\beta) &= \prod_{i=1}^{n} f(x_i) \\
&= \prod_{i=1}^{n} \frac{1}{\beta} e^{-\frac{x_i}{\beta}} \\
&= \frac{1}{\beta^{n}} \exp \left[ -\frac{1}{\beta} \sum_{i=1}^{n} x_i \right]
\end{align}
$$

上記に対し、対数尤度$l(\beta)=\log{L(\beta)}$は下記のように考えることができる。
$$
\large
\begin{align}
l(\beta) &= \log{L(\beta)} = \log{ \left( \frac{1}{\beta^{n}} \exp \left[ -\frac{1}{\beta} \sum_{i=1}^{n} x_i \right] \right) } \\
&= -n \log{\beta} – \frac{1}{\beta} \sum_{i=1}^{n} x_i \\
&= -n \log{\beta} – \frac{n \bar{x}}{\beta}
\end{align}
$$

上記を$\beta$で微分すると下記が得られる。
$$
\large
\begin{align}
\frac{\partial l(\beta)}{\partial \beta} &= -\frac{n}{\beta} + \frac{n \bar{x}}{\beta^2} \\
&= \frac{n(\bar{x}-\beta)}{\beta^2}
\end{align}
$$

上記より$\beta=\bar{x}$のとき$l(\beta)$は最大値を取るので、$\hat{\beta}=\overline{X}$のように最尤推定量を考えることができる。以下、$\bar{X}$が有効推定量であることを示す。$E[X_i], E[X_i^2]$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
E[X_i] &= \int_{0}^{\infty} x \times \frac{1}{\beta} e^{-\frac{x}{\beta}} dx \\
&= \left[ -x \cdot \frac{\cancel{\beta}}{\cancel{\beta}} e^{-\frac{x}{\beta}} \right]_{0}^{\infty} + \int_{0}^{\infty} e^{-\frac{x}{\beta}} dx \\
&= 0 – \left[ \beta e^{-\frac{x}{\beta}} \right]_{0}^{\infty} \\
&= -\beta(0-1) \\
&= \beta \\
E[X_i^2] &= \int_{0}^{\infty} x^2 \times \frac{1}{\beta} e^{-\frac{x}{\beta}} dx \\
&= \left[ -x^2 \cdot \frac{\cancel{\beta}}{\cancel{\beta}} e^{-\frac{x}{\beta}} \right]_{0}^{\infty} + 2 \beta \int_{0}^{\infty} x \times \frac{1}{\beta} e^{-\frac{x}{\beta}} dx \\
&= 0 + 2 \beta E[X_i] = 2 \beta^2
\end{align}
$$

上記より、$E[\overline{X}], V[\overline{X}]$は下記のように計算できる。
$$
\large
\begin{align}
E[\overline{X}] &= E \left[ \frac{1}{n} \sum_{i=1}^{n} X_i \right] \\
&= \frac{1}{n} \sum_{i=1}^{n} E[X_i] \\
&= \frac{1}{n} \times n \beta = \beta \\
V[\overline{X}] &= V \left[ \frac{1}{n} \sum_{i=1}^{n} X_i \right] \\
&= \frac{1}{n^2} \sum_{i=1}^{n} V[X_i] \\
&= \frac{1}{n^2} \times n V[X_i] \\
&= \frac{1}{n} (E[X_i^2] – E[X_i]^2) \\
&= \frac{1}{n}(2 \beta^2 – \beta^2) = \frac{\beta^2}{n}
\end{align}
$$

フィッシャー情報量を$I(\beta)$とおくと$I(\beta)$は下記のように表せる。
$$
\large
\begin{align}
I(\beta) &= -E \left[ \frac{\partial^2 l(\beta)}{\partial \beta^2} \right] \\
&= -E \left[ \frac{n}{\beta^2} – \frac{2n \bar{X}}{\beta^3} \right] \\
&= \frac{2n E[\bar{X}]}{\beta^3} – \frac{n}{\beta^2} \\
&= \frac{2n \beta}{\beta^3} – \frac{n}{\beta^2} \\
&= \frac{n}{\beta^2}
\end{align}
$$

よって下記が成立する。
$$
\large
\begin{align}
V[\overline{X}] = \frac{\beta^2}{n} = \left( \frac{n}{\beta^2} \right)^{-1} = I(\beta)^{-1}
\end{align}
$$

上記はクラメル・ラオの不等式の等号に対応するので、$\beta$の有効推定量は$\overline{X}$であると考えることができる。

問題8.2の解答例

問題8.3の解答例

問題8.4の解答例

まとめ

Ch.11 「ガンマ関数とベータ関数」の演習問題の解答例　〜統計学のための数学入門30講〜

投稿日: 2022-12-122023-02-06 投稿者: lib-arts

当記事は「統計学のための数学入門$30$講(朝倉書店)」の読解サポートにあたってChapter.$11$の「ガンマ関数とベータ関数」の章末問題の解答の作成を行いました。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

・書籍解答まとめ
https://www.hello-statisticians.com/answer_textbook

統計学のための数学入門30講 (科学のことばとしての数学)

Contents

1 本章のまとめ
- 1.1 ガンマ関数の定義と公式の導出
- 1.2 ベータ関数の定義と公式の導出
2 演習問題解答
- 2.1 問題$11.1$
- 2.2 問題$11.2$

本章のまとめ

ガンマ関数の定義と公式の導出

ガンマ関数$\Gamma(\alpha)$は下記のように定義される。
$$
\large
\begin{align}
\Gamma(\alpha) = \int_{0}^{\infty} x^{\alpha-1} e^{-x} dx \quad (1)
\end{align}
$$

ガンマ関数$\Gamma(\alpha)$に関して以下の式が成立する。
$$
\large
\begin{align}
\Gamma(\alpha+1) &= \alpha \Gamma(\alpha), \quad (2) \\
\Gamma(1) &= 1, \qquad (3) \\
\Gamma(n) &= (n-1)!, n \in \mathbb{N}, \quad (4) \\
\Gamma \left( \frac{1}{2} \right) &= \sqrt{\pi}, \qquad (5)
\end{align}
$$

以下、$(2)$〜$(5)$式が成立することをそれぞれ確認する。

・$(2)$式の導出
$(1)$式に基づいて$\Gamma(\alpha+1)$は下記のように変形できる。
$$
\large
\begin{align}
\Gamma(\alpha+1) &= \int_{0}^{\infty} x^{\alpha+1-1} e^{-x} dx \quad (1) \\
&= \int_{0}^{\infty} x^{\alpha} e^{-x} dx \\
&= \left[ -x^{\alpha} e^{-x} \right]_{0}^{\infty} + \alpha \int_{0}^{\infty} x^{\alpha-1} e^{-x} dx \\
&= 0 + \alpha \int_{0}^{\infty} x^{\alpha-1} e^{-x} dx \\
&= \alpha \Gamma(\alpha), \quad (2)
\end{align}
$$

・$(3)$式の導出
$(1)$式に基づいて$\Gamma(1)$は下記のように変形できる。
$$
\large
\begin{align}
\Gamma(1) &= \int_{0}^{\infty} x^{1-1} e^{-x} dx \quad (1) \\
&= \int_{0}^{\infty} e^{-x} dx \\
&= \left[ -e^{-x} \right]_{0}^{\infty} = -(0-1) = 1, \quad (3)
\end{align}
$$

・$(4)$式の導出
$n \in \mathbb{N}$のとき、$(2)$式を繰り返し用いたのちに$(3)$式を用いることで下記が得られる。
$$
\large
\begin{align}
\Gamma(n) &= (n-1) \Gamma(n-1) \\
&= \cdots \\
&= (n-1)! \Gamma(1) = (n-1)!, \quad (4)
\end{align}
$$

・$(5)$式の導出
$(1)$式より、$\displaystyle \Gamma \left( \frac{1}{2} \right)$は下記のように表せる。
$$
\large
\begin{align}
\Gamma \left( \frac{1}{2} \right) &= \int_{0}^{\infty} x^{\frac{1}{2}-1} e^{-x} dx \\
&= \int_{0}^{\infty} x^{-\frac{1}{2}} e^{-x} dx
\end{align}
$$

ここで上記に対し、$\displaystyle x = \frac{t^2}{2}$を考えると、$dx = t dt$が成立する。また、$x$と$t$の範囲の対応は下記のように考えられる。

$x$	$0 \to \infty$
$t$	$0 \to \infty$

よって$\displaystyle \Gamma \left( \frac{1}{2} \right)$は置換積分法を用いて下記のように変形できる。
$$
\large
\begin{align}
\Gamma \left( \frac{1}{2} \right) &= \int_{0}^{\infty} x^{-\frac{1}{2}} e^{-x} dx \\
&= \int_{0}^{\infty} \left( \frac{t^2}{2} \right)^{-\frac{1}{2}} e^{-\frac{t^2}{2}} \cdot t dt \\
&= \int_{0}^{\infty} \frac{\sqrt{2}}{\cancel{t}} e^{-\frac{t^2}{2}} \cdot \cancel{t} dt \\
&= \frac{1}{2} \int_{-\infty}^{\infty} \sqrt{2} e^{-\frac{t^2}{2}} dt \\
&= \sqrt{\pi} \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} e^{-\frac{t^2}{2}} dt \\
&= \sqrt{\pi}
\end{align}
$$

途中計算では標準正規分布$\mathcal{N}(0,1)$の全範囲での積分が$1$であることを用いた。標準正規分布の積分に関する導出の詳細は下記で取り扱った。

ガウス積分(Gaussian integral)の導出と標準正規分布の規格化

ベータ関数の定義と公式の導出

ベータ関数$B(\alpha,\beta)$は下記のように定義される。
$$
\large
\begin{align}
B(\alpha,\beta) = \int_{0}^{\infty} x^{\alpha-1} (1-x)^{\beta-1} dx \quad (6)
\end{align}
$$

ベータ関数$B(\alpha,\beta)$に関して以下の式が成立する。
$$
\large
\begin{align}
B(\alpha,\beta) &= B(\beta,\alpha), \quad (7) \\
B(\alpha,\beta) &= \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}, \quad (8) \\
\Gamma(m,n) &= \frac{(m-1)!(n-1)!}{(m+n-1)!}, m,n \in \mathbb{N}, \quad (9)
\end{align}
$$

以下、$(7)$〜$(9)$式が成立することをそれぞれ確認する。

演習問題解答

問題$11.1$

・$[1]$
前節の$(4)$式より、下記が得られる。
$$
\large
\begin{align}
\Gamma(4) = 3! = 6
\end{align}
$$

・$[2]$
前節の$(2)$式と$(5)$式より下記が得られる。
$$
\large
\begin{align}
\Gamma \left( \frac{5}{2} \right) &= \frac{3}{2} \cdot \frac{1}{2} \Gamma \left( \frac{1}{2} \right) \\
&= \frac{3}{4} \sqrt{\pi}
\end{align}
$$

・$[3]$
前節の$(8)$式より下記が得られる。
$$
\large
\begin{align}
B(3,4) &= \frac{\Gamma(3)\Gamma(4)}{\Gamma(3+4)} \\
&= \frac{2! \times 3!}{6!} \\
&= \frac{1}{60}
\end{align}
$$

・$[4]$
前節の$(8)$式と$(5)$式より下記が得られる。
$$
\large
\begin{align}
B \left( \frac{1}{2},\frac{1}{2} \right) &= \frac{\displaystyle \Gamma \left( \frac{1}{2} \right) \Gamma \left( \frac{1}{2} \right)}{\displaystyle \Gamma \left( \frac{1}{2}+\frac{1}{2} \right)} \\
&= \frac{\sqrt{\pi} \times \sqrt{\pi}}{\Gamma(1)} \\
&= \pi
\end{align}
$$

問題$11.2$

・$[1]$
下記のように定積分を計算することができる。
$$
\large
\begin{align}
\int_{0}^{\infty} y^{5} e^{-2y} dy &= \left[ -\frac{1}{2}y^{5}e^{-2y} \right]_{0}^{\infty} + \frac{5}{2} \int_{0}^{\infty} y^{4} e^{-2y} dy \\
&= 0 + \frac{5}{2} \int_{0}^{\infty} y^{4} e^{-2y} dy \\
&= \cdots \\
&= \frac{5!}{2^5} \int_{0}^{\infty} e^{-2y} dy \\
&= \frac{5!}{2^5} \left[ -\frac{1}{2}e^{-2y} \right]_{0}^{\infty} \\
&= \frac{5!}{2^6} = \frac{15}{8}
\end{align}
$$

・$[2]$
ガンマ分布$\displaystyle \Gamma \left( \frac{7}{2}, 2 \right)$の確率密度関数$f(y)$は下記のように表せる。
$$
\large
\begin{align}
f(y) = \frac{1}{\displaystyle 2^{\frac{7}{2}} \Gamma \left( \frac{7}{2} \right)} y^{\frac{7}{2}-1} e^{-\frac{y}{2}}
\end{align}
$$

上記の全区間での積分が$1$であることから、下記のように定積分を計算できる。
$$
\large
\begin{align}
\int_{0}^{\infty} y^{\frac{5}{2}} e^{-\frac{y}{2}} dy &= \int_{0}^{\infty} y^{\frac{7}{2}-1} e^{-\frac{y}{2}} dy \\
&= 2^{\frac{7}{2}} \Gamma \left( \frac{7}{2} \right) \\
&= \frac{5 \cdot 3 \cdot 1}{2^3} \times \sqrt{\pi} \times 2^{\frac{7}{2}} = 15 \sqrt{2 \pi}
\end{align}
$$

【統計の森独自評価】統計学・数学などの参考書のレビュー〜チャート式大学教養微分積分〜

投稿日: 2022-12-112022-12-01 投稿者: lib-arts

当記事では「チャート式シリーズ大学教養微分積分(数研出版)」のレビューに関して取りまとめを行いました。

・参考書籍一覧
https://www.hello-statisticians.com/uncategorized/reference.html

チャート式シリーズ大学教養微分積分 (チャート式・シリーズ)

3,080円(11/05 18:48時点)

Contents

1 レビューまとめ
- 1.1 Bestレビュー
- 1.2 「統計の森」運営レビュー
2 読み進める際の参考事項まとめ

レビューまとめ

Bestレビュー

「統計の森」運営レビュー

全体評価： $5.0$
統計学の参考書では数式の展開が省略されることが多いので、基本的な数学は別途抑えておく必要があるが、大学教養の微分積分に関しては「フォーマルで確認が大変な一般的な教科書」か「よくわかる〇〇のような概略のみの参考書」が多いように思われる。
一方で「チャート式シリーズ大学教養微分積分」では問題集の形式で抑えておくとよい点についてシンプルにまとめられており、大学教養レベルの微分積分の習得や復習に大変有用である。特に統計学に独学で取り組む際に大学教養レベルの数学が難しいなら同時に取り組んでおくと良い。
また、当書は数学検定$1$級の内容に概ね対応しているので、数学検定$1$級の対策にも用いることができる。準$1$級以前の内容に取り組む場合は高校数学に対応するチャート式や「統計学のための数学入門$30$講」などを合わせて入手するのも良い。

読み進める際の参考事項まとめ

Ch.10 「定積分の計算」の演習問題の解答例　〜統計学のための数学入門30講(朝倉書店)〜

投稿日: 2022-12-102022-12-03 投稿者: lib-arts

当記事は「統計学のための数学入門$30$講(朝倉書店)」の読解サポートにあたってChapter.$10$の「定積分の計算」の章末問題の解答の作成を行いました。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

・書籍解答まとめ
https://www.hello-statisticians.com/answer_textbook_math#math_stat

統計学のための数学入門30講 (科学のことばとしての数学)

Contents

1 本章のまとめ
2 演習問題解答
- 2.1 問題$10.1$
- 2.2 問題$10.2$

本章のまとめ

演習問題解答

問題$10.1$

・$[1]$
部分積分法に基づいて下記のように定積分の計算を行うことができる。
$$
\large
\begin{align}
\int_{1}^{2} x \log{x} dx &= \left[ \frac{1}{2} x^2 \log{x} \right]_{1}^{2} – \frac{1}{2} \int_{1}^{2} x^2 \cdot \frac{1}{x} dx \\
&= 2 \log{x} – \frac{1}{2^2} \left[ x^2 \right]_{1}^{2} \\
&= 2 \log{x} – \frac{3}{4}
\end{align}
$$

・$[2]$
下記のように定積分の計算を行うことができる。
$$
\large
\begin{align}
\int_{0}^{1} x (1-x)^{4} dx &= \left[ -\frac{1}{5} x (1-x)^{5} \right]_{0}^{1} + \frac{1}{5} \int_{0}^{1} (1-x)^{5} dx \\
&= 0 – \frac{1}{5 \cdot 6} \left[ (1-x)^{6} \right]_{0}^{1} \\
&= \frac{1}{30}
\end{align}
$$

問題$10.2$

・$[1]$
$$
\large
\begin{align}
\int_{0}^{1} x \sqrt{x^2+1} dx &= \frac{1}{2} \int_{0}^{1} (x^2+1)^{\frac{1}{2}} (x^2+1)’ dx \\
&= \frac{1}{\cancel{2}} \left[ \frac{\cancel{2}}{3} (x^2+1)^{\frac{3}{2}} \right]_{0}^{1} \\
&= \frac{1}{3}(2^{\frac{3}{2}}-1^{\frac{3}{2}}) = \frac{1}{3}(2\sqrt{2}-1)
\end{align}
$$

・$[2]$
$t = 1+\sqrt{x}$とおくと、$x=(t-1)^{2}, dx = 2(t-1) dt$が同時に成立する。また、$x$と$t$の値は下記のように対応する。

$x$	$0 \to 1$
$t$	$1 \to 2$

このとき置換積分法を用いて定積分は下記のように計算できる。
$$
\large
\begin{align}
\int_{0}^{1} \log{(1+\sqrt{x})} dx &= \int_{1}^{2} \log{t} \cdot 2(t-1) dt \\
&= \int_{1}^{2} ((t-1)^{2})’ \log{t} dt \\
&= \left[ (t-1)^{2} \log{t} \right]_{1}^{2} – \int_{1}^{2} \frac{(t-1)^2}{t} dt \\
&= \log{2} – \left[ \frac{1}{2}t^2 – 2t + \log{t} \right]_{1}^{2} \\
&= \cancel{\log{2}} – \left[ \left( 2 – 4 + \cancel{\log{2}} \right) – \left( \frac{1}{2} – 2 \right) \right] \\
&= \frac{1}{2}
\end{align}
$$

統計学のための数学入門30講 (科学のことばとしての数学)

ユニタリ行列(Unitary matrix)の定義とユニタリ行列の性質

投稿日: 2022-12-092022-11-29 投稿者: lib-arts

ユニタリ行列(Unitary matrix)は転置行列と逆行列が一致する直交行列に複素数(Complex Number)の取り扱いを加えて拡張した行列です。当記事では直行行列とユニタリ行列の定義と性質に関して演習などを通して具体的に取りまとめを行いました。
作成にあたっては、「チャート式シリーズ大学教養線形代数」の第$7$章「内積」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ大学教養線形代数 (チャート式・シリーズ)

3,080円(11/05 16:08時点)

Contents

1 ユニタリ行列の概要
2 ユニタリ行列の性質
- 2.1 重要例題$074$

ユニタリ行列の概要

直交行列

行列$A$が直交行列であるとき、直交行列の転置$A^{\mathrm{T}}$と単位行列$I$に関して下記が成立する。
$$
\large
\begin{align}
A A^{\mathrm{T}} = A^{\mathrm{T}} A = I
\end{align}
$$

上記より直交行列$A$に関して$A^{\mathrm{T}}=A^{-1}$も成立する。直交行列は下記のように多次元正規分布における$\exp$の内側に出てくる二次形式の解釈などに出てくるので抑えておくとよい。

多次元正規分布と二次形式(Mahalanobis distance)の直感的な理解

随伴行列

複素数を成分に持つ行列$A$に関して随伴行列(Adjoint matrix)は$A = \overline{A^{\mathrm{T}}}$のように定められる。$A=(a_{ij})$のように表記するなら共役な複素数を元に$A^{*}=(\overline{a_{ji}})$のように表せる。詳しくは下記で取り扱った。

随伴行列(Adjoint matrix)の定義と随伴行列の性質

ユニタリ行列の定義

行列$A$がユニタリ行列であるとき、ユニタリ行列の随伴行列$A^{*}$と単位行列$I$に関して下記が成立する。
$$
\large
\begin{align} A A^{*} = A^{*} A = I
\end{align}
$$

上記より$A^{*}=A^{-1}$も同時に成立する。

ユニタリ行列の性質

以下、「チャート式シリーズ大学教養線形代数」の例題の確認を行う。

重要例題$074$

・$(1)$
$[1]$
単位行列$I$に関して$I^{*}=I$が成立する。よって$I^{*}I=I$が成立するので単位行列はユニタリ行列である。

$[2]$
ユニタリ行列$U$と$V$を考えるとそれぞれ$U^{*}=U^{-1}, V^{*}=V^{-1}$が成立する。よって下記が成り立つ。
$$
\large
\begin{align}
(UV)^{*} = V^{*}U^{*} = V^{-1}U^{-1} = (UV)^{-1}
\end{align}
$$

$(UV)^{*} = (UV)^{-1}$が成立するので$UV$はユニタリ行列である。

$[3]$
ユニタリ行列$U$を考えると$U^{-1}$が成立する。このとき下記が成り立つ。
$$
\large
\begin{align}
(U^{-1})^{*} = (U^{*})^{*} = U = (U^{-1})^{-1}
\end{align}
$$

$(U^{-1})^{*} = (U^{-1})^{-1}$が成立するので$U^{-1}$はユニタリ行列である。

$[2]$
直交行列$U$と$V$を考えるとそれぞれ$U^{\mathrm{T}}=U^{-1}, V^{\mathrm{T}}=V^{-1}$が成立する。よって下記が成り立つ。
$$
\large
\begin{align}
(UV)^{\mathrm{T}} = V^{\mathrm{T}}U^{\mathrm{T}} = V^{-1}U^{-1} = (UV)^{-1}
\end{align}
$$

$(UV)^{\mathrm{T}} = (UV)^{-1}$が成立するので$UV$は直交行列である。

$[3]$
直交行列$U$を考えると$U^{-1}$が成立する。このとき下記が成り立つ。
$$
\large
\begin{align}
(U^{-1})^{\mathrm{T}} = (U^{\mathrm{T}})^{\mathrm{T}} = U = (U^{-1})^{-1}
\end{align}
$$

$(U^{-1})^{\mathrm{T}} = (U^{-1})^{-1}$が成立するので$U^{-1}$は直交行列である。

チャート式シリーズ大学教養線形代数 (チャート式・シリーズ)

3,080円(11/05 16:08時点)

Ch.9 「定積分」の演習問題の解答例　〜統計学のための数学入門30講(朝倉書店)〜

投稿日: 2022-12-082022-12-03 投稿者: lib-arts

当記事は「統計学のための数学入門$30$講(朝倉書店)」の読解サポートにあたってChapter.$9$の「定積分」の章末問題の解答の作成を行いました。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

・書籍解答まとめ
https://www.hello-statisticians.com/answer_textbook_math#math_stat

統計学のための数学入門30講 (科学のことばとしての数学)

Contents

1 本章のまとめ
2 演習問題解答
- 2.1 問題$9.1$
- 2.2 問題$9.2$

本章のまとめ

演習問題解答

問題$9.1$

・$[1]$
$f(x)=e^{-2x}$の原始関数を$F(x)$とおくと$F'(x)=f(x)$が成立する。このとき、下記のように考えることができる。
$$
\large
\begin{align}
\frac{d}{dx} \int_{a}^{x} e^{-2t} dt &= \frac{d}{dx} \int_{a}^{x} f(t) dt \\
&= \frac{d}{dx} (F(x) – F(a)) \\
&= f(x) = e^{-2x}
\end{align}
$$

・$[2]$
$f(x)=e^{-2x}-7x$の原始関数を$F(x)$とおくと$F'(x)=f(x)$が成立する。このとき、下記のように考えることができる。
$$
\large
\begin{align}
\frac{d}{dx} \int_{a}^{x^2} (e^{-2t}-7t) dt &= \frac{d}{dx} \int_{a}^{x^2} f(t) dt \\
&= \frac{d}{dx} (F(x^2) – F(a)) \\
&= f(x^2) \times (x^2)’ = 2x (e^{-2x^2}-7x^2)
\end{align}
$$

問題$9.2$

統計検定準1級問題解説～2017年6月実施選択問題及び部分記述問題問10～

投稿日: 2022-12-072023-01-16 投稿者: hello-stat

Contents

1 過去問題
2 解答
- 2.1 [1] 解答
- 2.2 [2] 解答

過去問題

過去問題は統計検定公式が問題と解答例を公開しています。こちらを参照してください。

日本統計学会公式認定統計検定準1級公式問題集

3,300円(11/05 23:44時点)

解答

[1] 解答

(1) $\boxed{ \ \mathsf{12}\ }$ : ③

男性の就業者数の期待度数を$x$，女性の就業者数の期待度数を$y$ とすると，次の表を得る．

$$
\begin{array}{cccc}
& 就業者 & 非就業者 & 計 \\
\hline
\text{男} & x & 41-x & 41 & \\
\hline
\text{女} & y & 3-y & 39 & \\
\hline
\text{計} & 68 & 12 & 80 &
\hline
\end{array}
$$

また，問題文の条件から$x$，$y$は次を満たせば良い．
$$
   \begin{align}
       \left\{
       \begin{array}{l}
       x+y=68 \\
       \dfrac{x}{41} = \dfrac{y}{39}
       \end{array}
       \right.
   \end{align}
$$

これを解いて，

   \[
       y = \dfrac{39\times 68}{80} = 33.15
   \]

を得る．

(2) $\boxed{ \ \mathsf{13}\ }$ : ③

イエーツの補正をした$\chi^2$統計量を$\chi^2$と表すことにすると，
   \[
       \chi^2 = \dfrac{80(|39\cdot9 – 3\cdot30|-80/2)^2}{41\cdot 39 \cdot 68 \cdot 12} \approx 2.76
   \]

である．ここで，自由度1の$\chi^2$分布について，上側$1\%$点は$6.63$，上側$5\%$点は$3.84$，上側$10\%$点は$2.71$，であるから有意水準$1\%$，$5\%$ では棄却されず，$10\%$ では棄却される．

[2] 解答

$\boxed{ \ \mathsf{14}\ }$ : ①

男性で就業者の人数が$x$人になるのは，$38$人から$x$人を選び，それ以外の$42$人から$30-x$人を選ぶ時なので，その確率は

   \[
       \dfrac{_{38}C_{x} \cdot _{42}C_{30-x}}{_{80}C_{30}}
   \]

である．

統計検定準1級問題解説～2017年6月実施選択問題及び部分記述問題問9～

投稿日: 2022-12-072022-12-08 投稿者: hello-stat

Contents

1 過去問題
2 解答
- 2.1 [1] 解答
- 2.2 [2] 解答

過去問題

過去問題は統計検定公式が問題と解答例を公開しています。こちらを参照してください。

日本統計学会公式認定統計検定準1級公式問題集

3,300円(11/05 23:44時点)