数式だけの解説ではわかりにくい場合もあると思われるので、統計学の手法や関連する概念をPythonのプログラミングで表現します。当記事では二項分布の極限を取扱う際に出てくるポアソンの小数の法則と中心極限定理(Central Limit Theory)に関して取り扱います。
・Pythonを用いた統計学のプログラミングまとめ
https://www.hello-statisticians.com/stat_program
Contents
二項分布
問題設定と二項分布の確率関数
二項分布ではコイン投げのような2値を取るベルヌーイ試行を一定の確率$p$で$n$回繰り返しを行なった際に、確率pの事象が観測される回数を確率変数Xで表し、$X=k, k=0,1,2,…,n$の確率を考える。この確率関数を$P(X=k)$のように表すとき、$P(X=k)$は下記のような式で表すことができる。
$$
\large
\begin{align}
P(X=k) = {}_{n} C_{k} p^{k} (1-p)^{n-k}
\end{align}
$$
ベルヌーイ試行を確率$p$で$n$回繰り返す際に対応する二項分布は$Bin(n,p)$で表されることが多い。
確率分布の描画
$$
\large
\begin{align}
P(X=k) = {}_{n} C_{k} p^{k} (1-p)^{n-k}
\end{align}
$$
二項分布$Bin(n,p)$の確率関数は上記のように表される。式の形だけでは難しく見えるので以下具体的な$n$と$p$の値を元に二項分布の確率関数に基づく描画を行う。
import math
import numpy as np
import matplotlib.pyplot as plt
def comb(n,r):
res = math.factorial(n)/(math.factorial(n-r)*math.factorial(r))
return float(res)
n = np.array([10., 10., 10., 20.])
p = np.array([0.5, 0.1, 0.7, 0.5])
for i in range(n.shape[0]):
x = np.arange(0,n[i]+1,1)
y = np.zeros(n[i]+1)
for j in range(x.shape[0]):
y[j] = comb(n[i],j) * p[i]**j * (1-p[i])**(n[i]-j)
plt.subplot(2,2,i+1)
plt.title("(n,p): ({:.0f},{:.1f})".format(n[i],p[i]))
plt.bar(x,y,color="limegreen")
plt.show()・実行結果
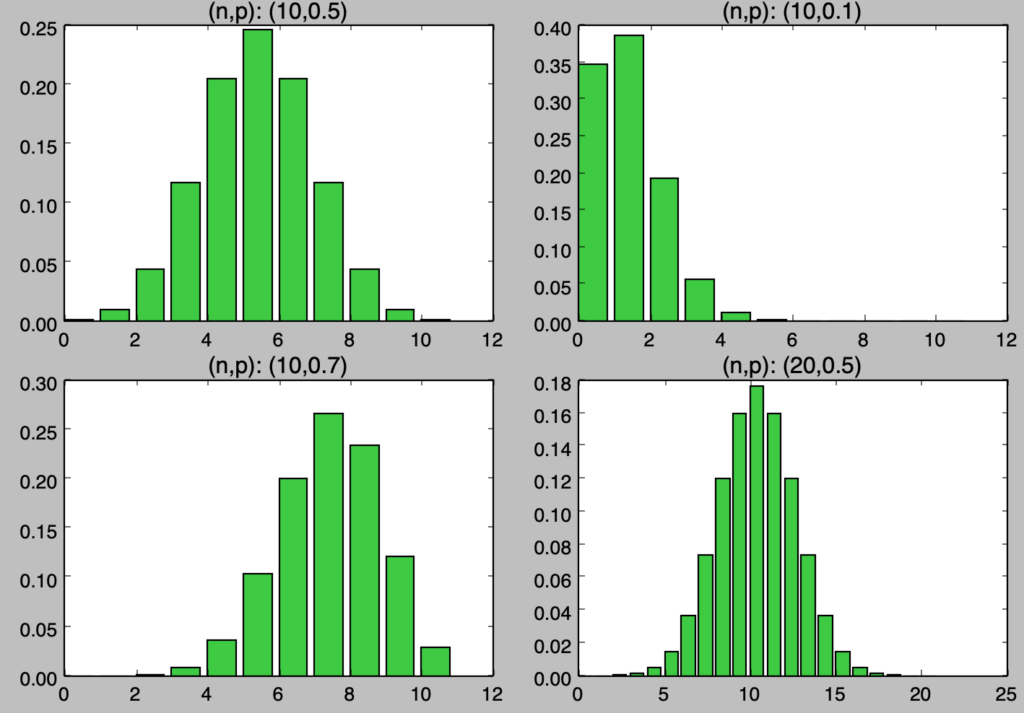
二項分布の確率分布は上記のように描画を行うことができる。二項分布では確率変数$X$に対して$E[X]=np$が成立するが、どの分布でも$np$が概ね平均を表すであろうことは読み取れる。$p$を大きくするにつれて平均が右にシフトすることもわかる。
また、$n$の数が大きくなると確率変数の取りうる範囲が大きくなることもわかる。当記事では$n$の極限を考えるので、右下の図で表したように$n$が大きくなると確率変数の取り得る値が多くなり、取り扱いが段々と難しくなることは抑えておくと良い。
ポアソンの小数の法則
問題設定
基本的には「二項分布」で取り扱った問題設定と同様だが、$n=1000, p=0.002$のように$n$が大きい一方で$p$が小さい分布に関して考える。ここで$np$を概ね一定とみなし、$\lambda=np$とおく。
二項分布を用いる際の課題
$n=1000, p=0.002$の際の二項分布に関して考える。二項分布の基本的な考え方に基づいて考えると、確率変数$X$に対して$0$〜$1000$の値を考えれば良いので、以下この考え方に基づいて計算を行う。
import math
import numpy as np
import matplotlib.pyplot as plt
def comb(n,r):
res = math.factorial(n)/(math.factorial(n-r)*math.factorial(r))
return float(res)
n = 1000
p = 0.002
x = np.arange(0,n+1,1)
y = np.zeros(n+1)
display_num = np.array([10,20,50,100])
# 計算に時間がかかる場合はnを小さく変更してください
for i in range(x.shape[0]):
y[i] = comb(n,i) * p**i * (1-p)**(n-i)
for i in range(4):
plt.subplot(2,2,i+1)
plt.title("X: 0-{:.0f}".format(display_num[i]))
plt.bar(x[:(display_num[i]+1)],y[:(display_num[i]+1)],color="limegreen")
plt.show()・実行結果
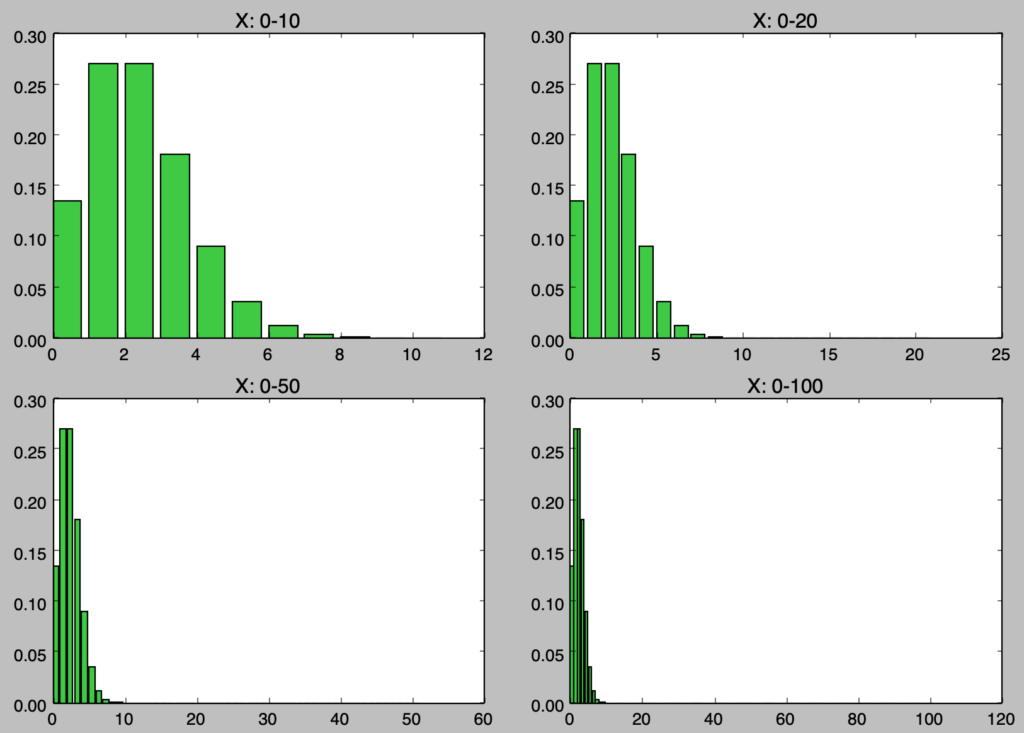
実行結果より、大半の確率が$X=0$から$X=10$までに対応することが読み取れる。これは$E[X]=np=2$であることからも理解することができる。display_numで表示する変数の数を切り替えることで、$X=0$から$X=10$に確率が偏ることが理解しやすいと思われる。
また、計算にあたっては$1000$乗を計算していることで計算負荷が大きくなったり、桁数のエラーなどが生じたりする場合がある。このように$n$が大きくなるにつれて二項分布をそのまま用いるだけでは計算が多い一方で得るものが少ない。
このような二項分布の課題に対し、考えられたのが「ポアソンの小数の法則」に基づいて導出される「ポアソン分布」である。次項で「ポアソン分布」を用いた「二項分布の近似」とその誤差に関して確認を行う。
ポアソン分布の描画と二項分布との近似誤差
前項では$n=1000, p=0.002$のように$n$が大きい一方で$p$が小さい場合に二項分布の取り扱いにおける課題の確認を行なった。この解決にあたっては「ポアソンの小数の法則」に基づく「ポアソン分布」が用いられることが多い。
$$
\large
\begin{align}
P(X=k) &= \frac{\lambda^{k} e^{-\lambda}}{k!} \\
\lambda &= np
\end{align}
$$
「ポアソン分布」の確率関数は上記のように表される。
「ポアソンの小数の法則」を用いた導出に関しては「ポアソン分布の演習」で詳しく取り扱ったのでここでは省略し、ポアソン分布の描画を行う。
import math
import numpy as np
import matplotlib.pyplot as plt
n, p = 1000, 0.002
lamb = n*p
x = np.arange(0,11,1)
y = np.zeros(11)
for i in range(x.shape[0]):
y[i] = lamb**i * np.e**(-lamb) / math.factorial(i)
plt.bar(x,y,color="limegreen")
plt.show()・実行結果
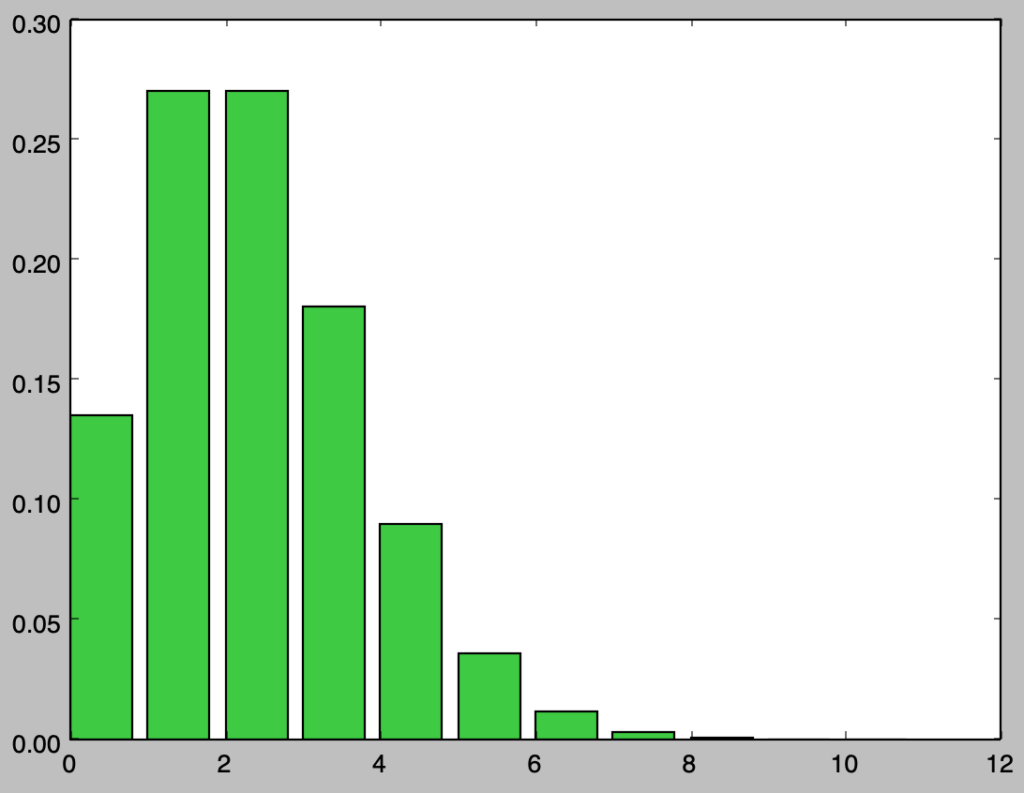
実行結果を確認すると、二項分布と概ね同様の結果が得られることが確認できる。以下、近似にあたっての誤差に関して確認を行う。
import math
import numpy as np
import matplotlib.pyplot as plt
def comb(n,r):
res = math.factorial(n)/(math.factorial(n-r)*math.factorial(r))
return float(res)
n, p = 1000, 0.002
lamb = n*p
x = np.arange(0,n+1,1)
y_bin, y_poisson = np.zeros(n+1), np.zeros(n+1)
# 計算に時間がかかる場合はnを小さく変更してください
for i in range(x.shape[0]):
y_bin[i] = comb(n,i) * p**i * (1-p)**(n-i)
y_poisson[i] = lamb**i * np.e**(-lamb) / math.factorial(i)
y_diff = y_bin - y_poisson
print(np.sum(np.abs(y_diff)))
plt.plot(x[:21],y_diff[:21])
plt.plot(x[:21],np.zeros(21))
plt.show()・実行結果
> print(np.sum(np.abs(y_diff)))
0.000903440009195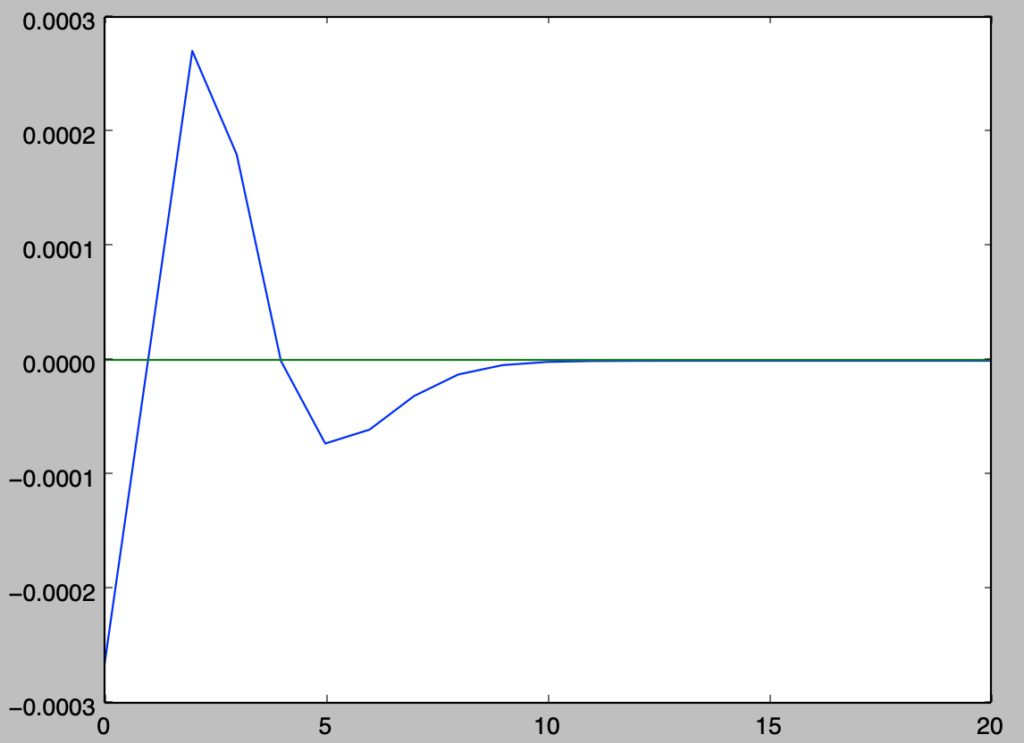
上記の結果より、誤差の絶対値の和が全確率の$1$の$0.09$%に対応することが確認できる。
中心極限定理
問題設定
基本的には「二項分布」で取り扱った問題設定と同様だが、$n=1000, p=0.3$のように$n$が大きい場合かつ、「ポアソン分布」の問題設定ほど$p$が小さくない場合を考える。
二項分布を用いる際の課題
$n=1000, p=0.3$の際の二項分布に関して考える。二項分布の基本的な考え方に基づいて考えると、確率変数$X$に対して$0$〜$1000$の値を考えれば良いので、以下この考え方に基づいて計算を行う。
import math
import numpy as np
import matplotlib.pyplot as plt
def comb(n,r):
res = math.factorial(n)/(math.factorial(n-r)*math.factorial(r))
return float(res)
n = 1000
p = 0.3
x = np.arange(0,n+1,1)
y = np.zeros(n+1)
# 計算に時間がかかる場合はnを小さく変更してください
for i in range(x.shape[0]):
y[i] = comb(n,i) * p**i * (1-p)**(n-i)
plt.bar(x[280:320],y[280:320],color="limegreen")
plt.show()・実行結果
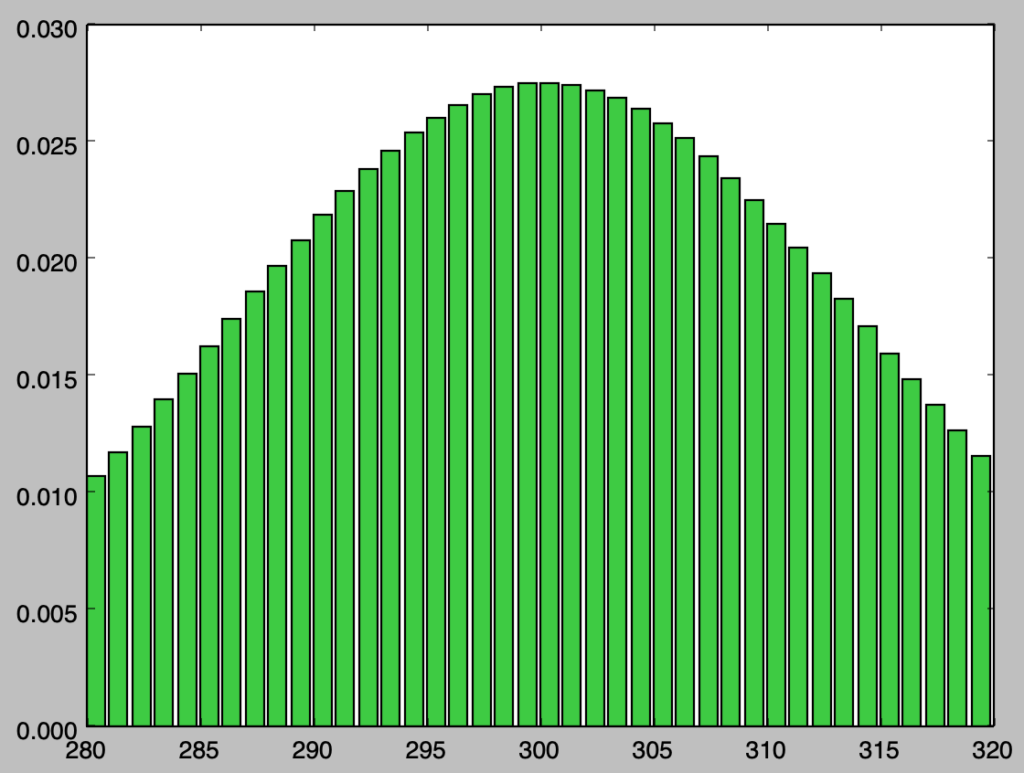
実行結果を確認すると、概ね正規分布のような形状をしていることが確認できる。実際の取り扱いではここで中心極限定理を考えることにより、$N(np,\sqrt{np(1-p)})$で近似することが多い。次項で「正規分布」を用いた「二項分布の近似」とその誤差に関して確認を行う。
正規分布の描画と二項分布との近似誤差
前項では$n=1000, p=0.3$のように$n$が大きい場合の二項分布の取り扱いにおける課題の確認を行なった。この解決にあたっては「中心極限定理」に基づいて「正規分布」が用いられることが多い。以下では離散型の確率変数に対応して正規分布の累積分布関数より二項分布の近似を考える。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
n, p = 1000, 0.3
lamb = n*p
x = np.arange(0,1000+1,1)
y = np.zeros(1000+1)
for i in range(x.shape[0]):
y[i] = stats.norm.cdf(i+0.5,loc=n*p,scale=np.sqrt(n*p*(1-p))) - stats.norm.cdf(i-0.5,loc=n*p,scale=np.sqrt(n*p*(1-p)))
plt.bar(x[280:320],y[280:320],color="limegreen")
plt.show()・実行結果
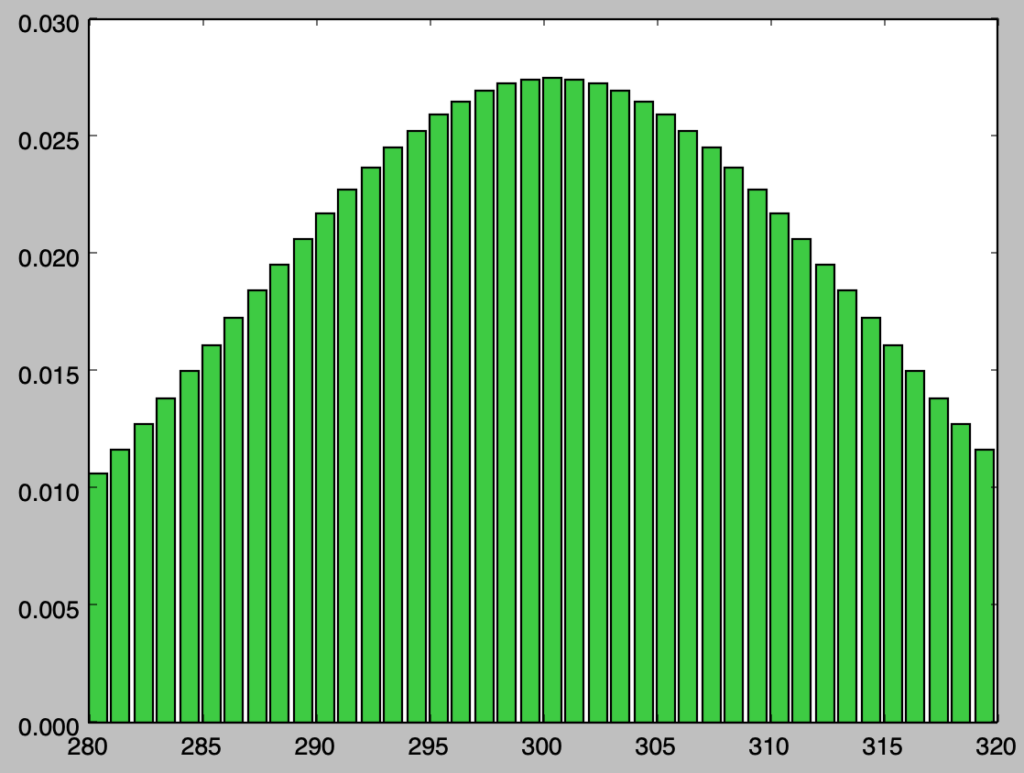
実行結果を確認すると、二項分布と概ね同様の結果が得られることが確認できる。途中の計算にあたっては連続修正の考えに基づき、stats.norm.cdf(i+0.5)-stats.norm.cdf(i-0.5)の計算を行なった。以下、近似にあたっての誤差に関して確認を行う。
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
def comb(n,r):
res = math.factorial(n)/(math.factorial(n-r)*math.factorial(r))
return float(res)
n, p = 1000, 0.3
lamb = n*p
x = np.arange(0,n+1,1)
y_bin, y_norm = np.zeros(n+1), np.zeros(n+1)
# 計算に時間がかかる場合はnを小さく変更してください
for i in range(x.shape[0]):
y_bin[i] = comb(n,i) * p**i * (1-p)**(n-i)
y_norm[i] = stats.norm.cdf(i+0.5,loc=n*p,scale=np.sqrt(n*p*(1-p))) - stats.norm.cdf(i-0.5,loc=n*p,scale=np.sqrt(n*p*(1-p)))
y_diff = y_bin - y_norm
print(np.sum(np.abs(y_diff)))
plt.plot(x[220:380],y_diff[220:380])
plt.plot(x[220:380],np.zeros(380-220))
plt.show()・実行結果
> print(np.sum(np.abs(y_diff)))
0.00694647548049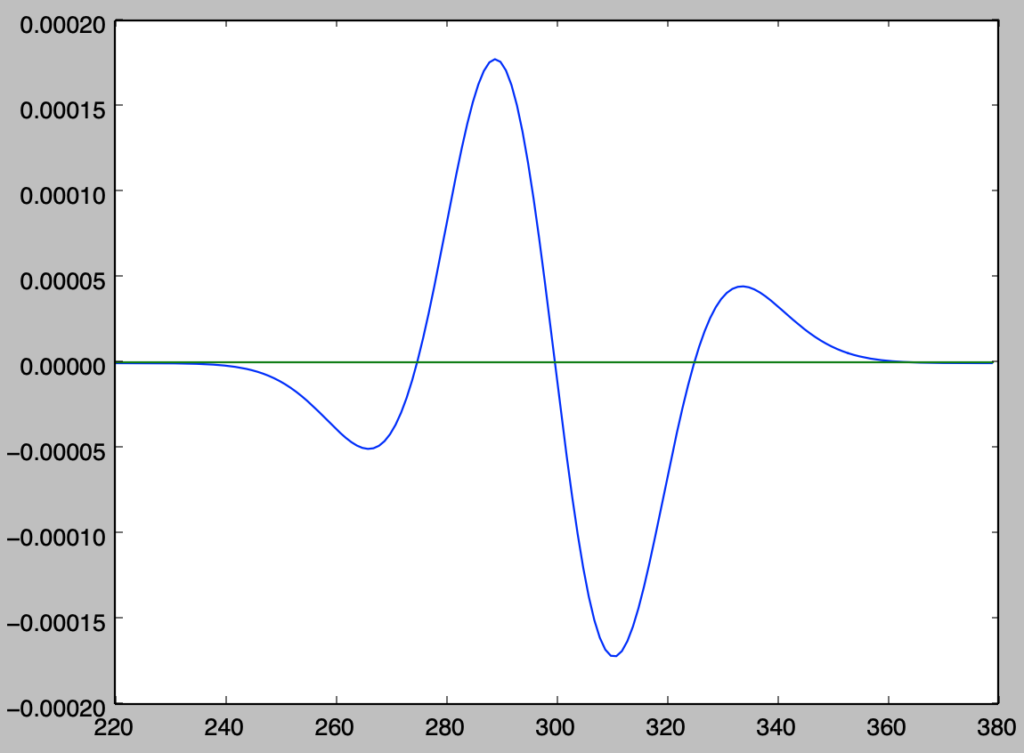
上記の結果より、誤差の絶対値の和が全確率の$1$の$0.6$%に対応することが確認できる。