数式だけの解説ではわかりにくい場合もあると思われるので、統計学の手法や関連する概念をPythonのプログラミングで表現します。当記事ではベイズ法の理解にあたって、共役事前分布などを用いて得た事後分布の描画やそれに基づくベイズ推定量、MAP推定量の値の確認を行います。
・Pythonを用いた統計学のプログラミングまとめ
https://www.hello-statisticians.com/stat_program
共役事前分布と事後分布を用いた推定
二項分布とベータ分布
ベータ分布の関数形
$$
\large
\begin{align}
f(x|a,b) &= \frac{1}{B(a,b)} x^{a-1} (1-x)^{b-1}, \quad 0 \leq x \leq 1 \\
B(a,b) &= \int_{0}^{1} x^{a-1} (1-x)^{b-1} dx
\end{align}
$$
ベータ分布$Be(a,b)$を考える際、確率密度関数は上記で表されるが、$\displaystyle B(a,b) = \frac{\gamma(a)\gamma(b)}{\gamma(a+b)}$のように考えることができるので、$a, b$が整数の時は$x^{a-1} (1-x)^{b-1}$の形状を中心に確認すれば良い。
以下、Pythonを用いて$x^{a-1} (1-x)^{b-1}$の形状や$\displaystyle \frac{1}{B(a,b)} = \frac{\gamma(a+b)}{\gamma(a)\gamma(b)}$の値の推移の確認を行う。
import math
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
a, b = np.array([1, 1, 3, 5, 10]), np.array([1, 3, 1, 5, 10])
x = np.arange(0., 1.01, 0.01)
y = np.zeros([x.shape[0], a.shape[0]])
for i in range(a.shape[0]):
y[:,i] = (math.factorial(a[i]+b[i]-1)/(math.factorial(a[i]-1)*math.factorial(b[i]-1))) * x**(a[i]-1) * (1-x)**(b[i]-1)
plt.plot(x,y[:,i],label="(a,b): ({:.0f},{:.0f})".format(a[i],b[i]))
print("1/B({},{}): {}".format(a[i],b[i],math.factorial(a[i]+b[i]-1)/(math.factorial(a[i]-1)*math.factorial(b[i]-1))))
plt.legend()
plt.show()・実行結果
1/B(1,1): 1
1/B(1,3): 3
1/B(3,1): 3
1/B(5,5): 630
1/B(10,10): 923780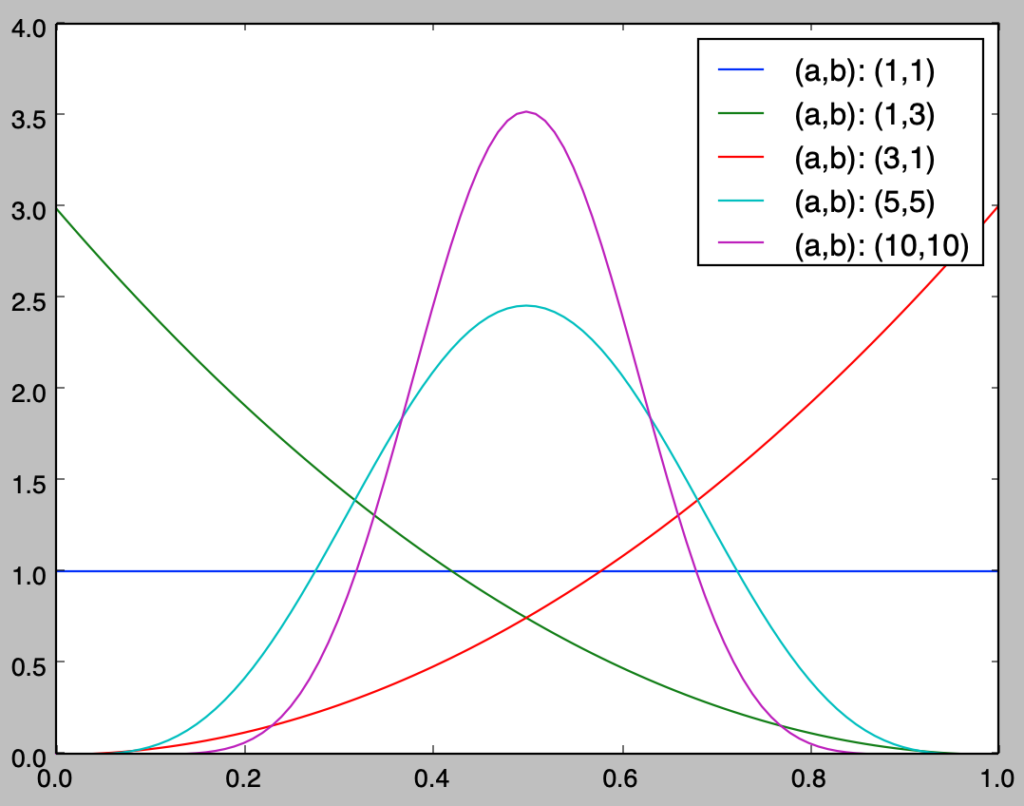
SciPyを用いたベータ分布の取り扱い
前項のように数式に基づいてベータ分布の作成を行うこともできるが、scipy.stats.betaを用いることで、ベータ分布に関して以下のように取り扱いを行うことも可能である。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
a, b = np.array([1, 1, 3, 5, 10]), np.array([1, 3, 1, 5, 10])
x = np.arange(0., 1.01, 0.01)
y = np.zeros([x.shape[0], a.shape[0]])
for i in range(a.shape[0]):
y[:,i] = stats.beta.pdf(x, a[i], b[i])
plt.plot(x,y[:,i],label="(a,b): ({:.0f},{:.0f})".format(a[i],b[i]))
plt.legend()
plt.show()・実行結果
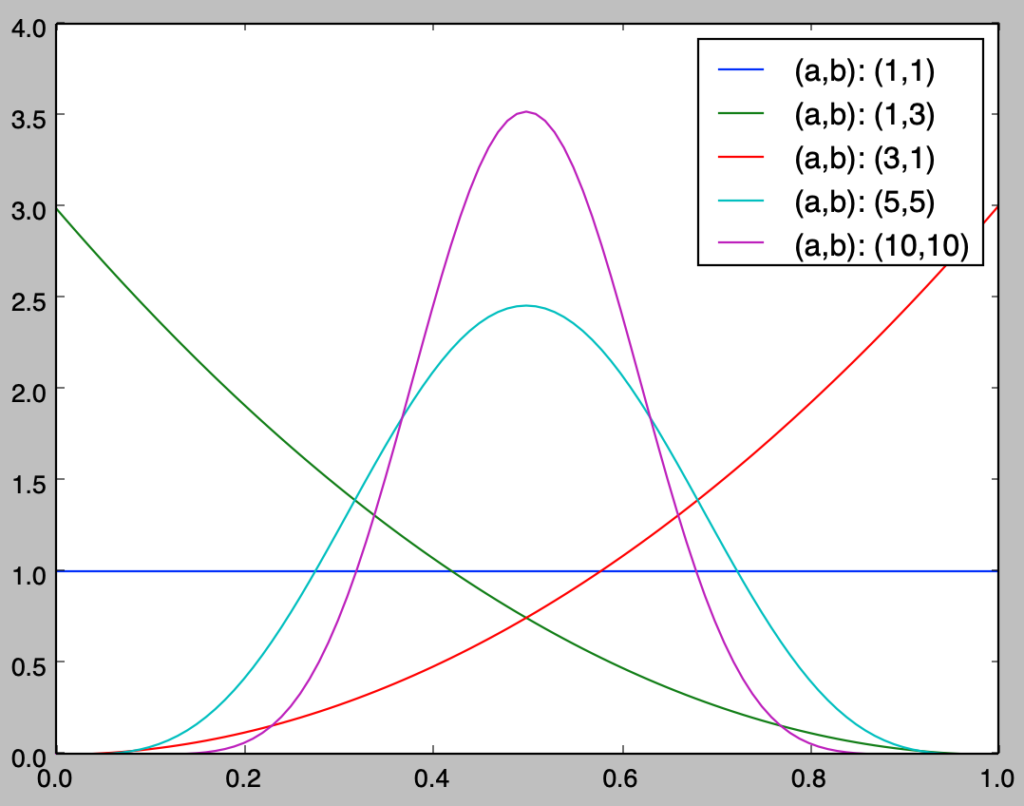
scipy.stats.betaを用いることで、前項と同様の結果が得られることを確認しておくと良い。
事後分布とベイズ推定・MAP推定
$n$回のベルヌーイ試行のうち、確率$p$の事象が観測された回数を$x$とおくと、事前分布$Be(a,b)$からは事後分布$Be(a+x,b+n-x)$が得られる。
$$
\large
\begin{align}
\hat{p}_{B} &= E[X] \\
&= \frac{a}{a+b} \\
\hat{p}_{MAP} &= \frac{a-1}{a+b-2}
\end{align}
$$
ここでベータ分布$Be(a,b)$に基づくイズ推定量を$\hat{p}_{B}$、MAP推定量を$\hat{p}_{MAP}$は上記のように表せることから、事後分布$Be(a+x,b+n-x)$に基づくベイズ推定量$\hat{p}_{B}$、MAP推定量$\hat{p}_{MAP}$は、それぞれ下記のように計算できる。
$$
\large
\begin{align}
\hat{p}_{B} &= E[X] \\
&= \frac{a+x}{a+x+b+n-x} \\
&= \frac{a+x}{a+b+n} \\
\hat{p}_{MAP} &= \frac{a+x-1}{a+x+b+n-x-2} \\
&= \frac{a+x-1}{a+b+n-2}
\end{align}
$$
上記を元に、いくつかの$Be(a+x,b+n-x)$のパターンに対して、事後分布と$\hat{p}_{B}, \hat{p}_{MAP}$の確認を行う。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
a, b = np.array([3., 2., 2., 5., 10., 10.]), np.array([2., 5., 10., 5., 20., 50.])
x = np.arange(0., 1.01, 0.01)
y = np.zeros([x.shape[0], a.shape[0]])
for i in range(6):
y[:,i] = stats.beta.pdf(x, a[i], b[i])
plt.subplot(2,3,i+1)
plt.plot(x,y[:,i],color="green")
plt.plot(np.repeat(a[i]/(a[i]+b[i]),20),np.linspace(0,stats.beta.pdf(a[i]/(a[i]+b[i]), a[i], b[i])-0.01,20),"b--", label="p_B")
plt.plot(np.repeat((a[i]-1.)/(a[i]+b[i]-2.),20),np.linspace(0,stats.beta.pdf((a[i]-1.)/(a[i]+b[i]-2.), a[i], b[i])-0.01,20),"r--", label="p_B")
plt.title("a+x={}, b+n-x={}".format(a[i],b[i]))
plt.legend(loc=4)
plt.show()・実行結果
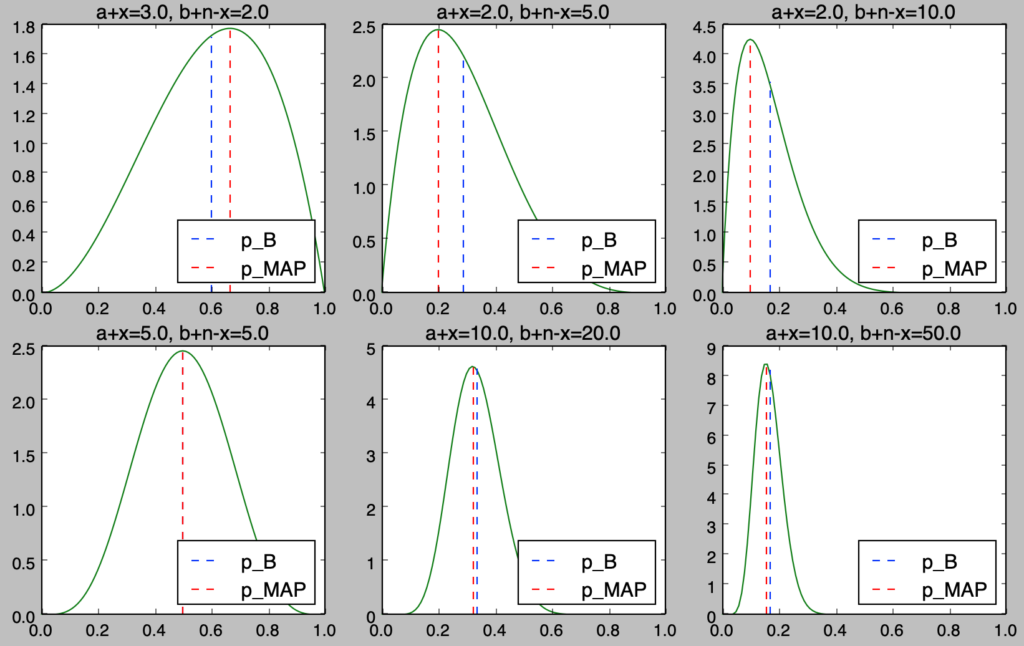
$a=1, b=1$の一様分布などを事前分布に考えるとき、上記の結果より、観測サンプルが多くなるにつれて推定結果が$x/n$に収束していくことが確認できる。また、ベイズ推定量とMAP推定量はそれぞれの推定値が$0.5$より大きいか小さいかによってどちらの推定値が大きいかが定まることも読み取れる。
ポアソン分布とガンマ分布
ガンマ分布の関数形
$$
\large
\begin{align}
f(x|\nu,\alpha) &= \frac{1}{\gamma(\nu) \alpha^{\nu}} x^{\nu-1} e^{-\frac{x}{\alpha}}, \quad 0 \leq x \\
\gamma(\nu) &= \frac{1}{\alpha^{\nu}} \int_{0}^{\infty} x^{\nu-1} e^{-\frac{x}{\alpha}} dx
\end{align}
$$
ガンマ分布$Ga(\nu,\alpha)$を考える際、確率密度関数は上記で表されるが、$\gamma(\nu), \alpha^{\nu}$は確率分布の規格化定数なので、$\displaystyle x^{\nu-1} e^{-\frac{x}{\alpha}}$の形状を中心に確認すれば良い。
以下、Pythonを用いて$\displaystyle x^{\nu-1} e^{-\frac{x}{\alpha}}$の形状や$\gamma(\nu), \alpha^{\nu}$の値の推移の確認を行う。
import math
import numpy as np
import matplotlib.pyplot as plt
nu, alpha = np.array([1, 2, 5, 10, 2]), np.array([1, 1, 1, 1, 2])
x = np.arange(0., 10.1, 0.1)
y = np.zeros([x.shape[0], nu.shape[0]])
for i in range(nu.shape[0]):
y[:,i] = x**(nu[i]-1) * np.e**(-x/alpha[i]) / (math.factorial(nu[i]-1)*alpha[i]**nu[i])
plt.plot(x,y[:,i],label="(nu,alpha): ({:.0f},{:.0f})".format(nu[i],alpha[i]))
print("gamma({}): {}, alpha^{}: {}".format(nu[i],math.factorial(nu[i]-1),alpha[i],alpha[i]**nu[i]))
plt.legend()
plt.show()・実行結果
gamma(1): 1, alpha^1: 1
gamma(2): 1, alpha^1: 1
gamma(5): 24, alpha^1: 1
gamma(10): 362880, alpha^1: 1
gamma(2): 1, alpha^2: 4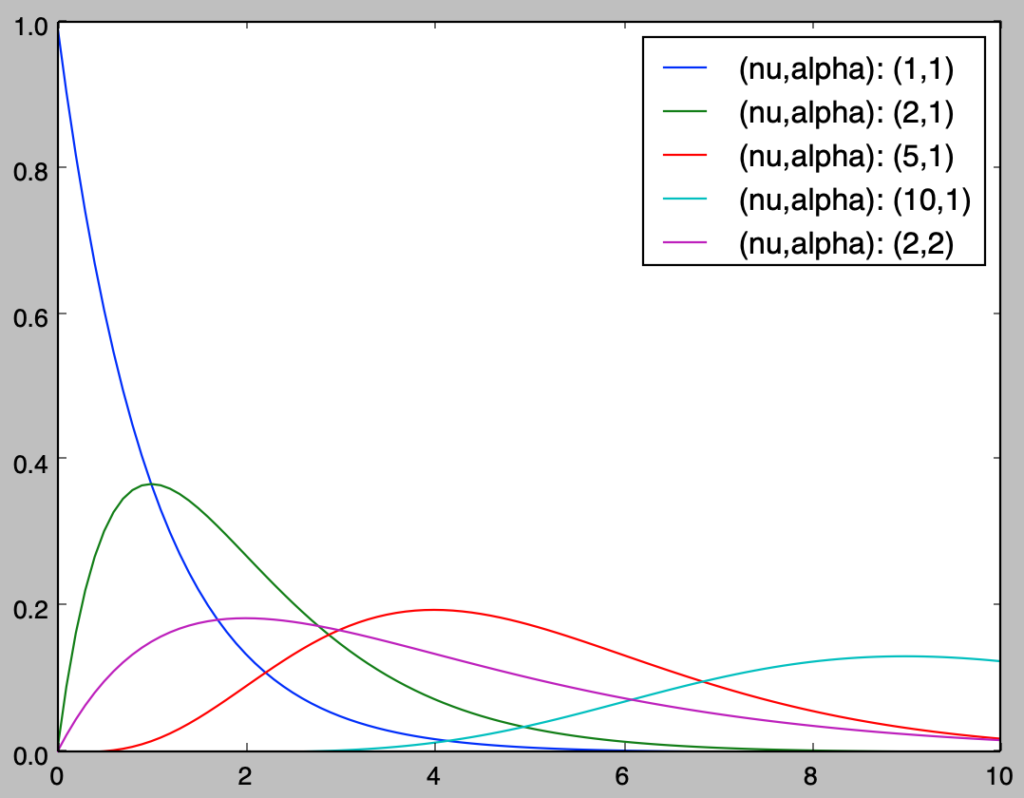
SciPyを用いたガンマ分布の取り扱い
前項のように数式に基づいてガンマ分布の作成を行うこともできるが、scipy.stats.gammaを用いることで、ガンマ分布に関して以下のように取り扱いを行うことも可能である。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
nu, alpha = np.array([1., 2., 5., 10., 2.]), np.array([1., 1., 1., 1., 2.])
x = np.arange(0., 10.1, 0.1)
y = np.zeros([x.shape[0], nu.shape[0]])
for i in range(nu.shape[0]):
y[:,i] = stats.gamma.pdf(x, a=nu[i], scale=alpha[i])
plt.plot(x,y[:,i],label="(nu,alpha): ({:.0f},{:.0f})".format(nu[i],alpha[i]))
plt.legend()
plt.show()・実行結果
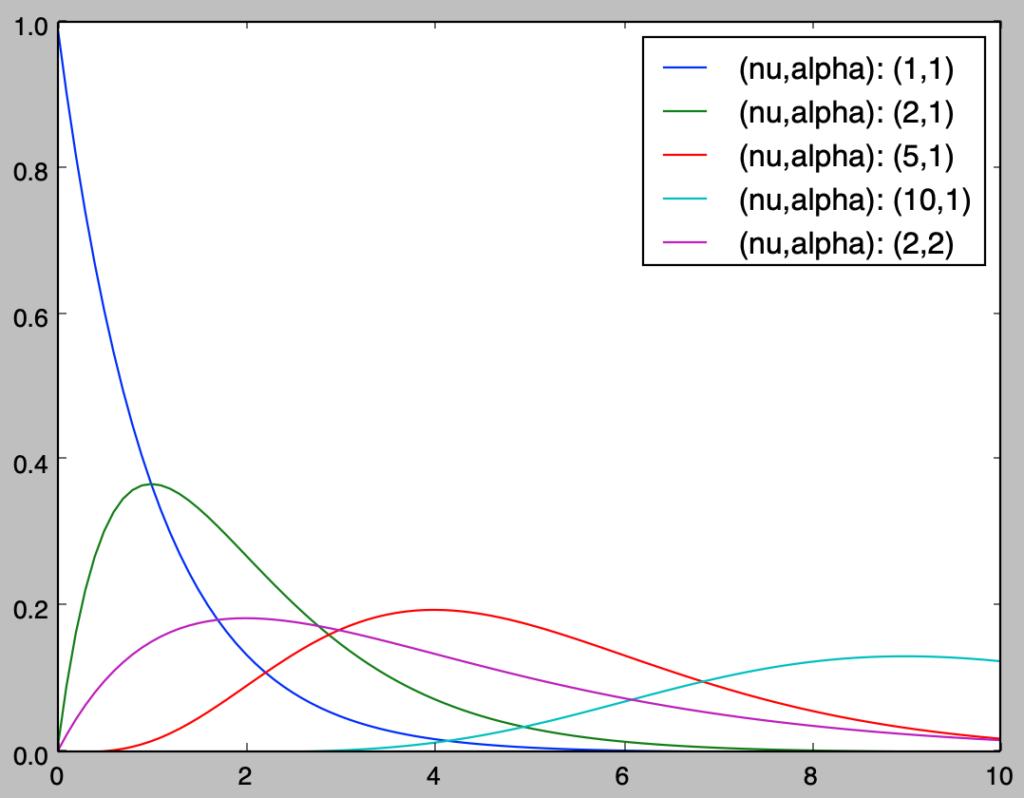
scipy.stats.gammaを用いることで、前項と同様の結果が得られることを確認しておくと良い。
事後分布とベイズ推定・MAP推定
平均を表すパラメータが$\lambda$のポアソン分布に従い、$x_1,x_2,…,x_n$が観測されたとき、事前分布$Ga(\nu,1/\beta)$からは事後分布$\displaystyle Ga(\nu+\sum_{i=1}^{n}x_i,1/(\beta+n))$が得られる。
$$
\large
\begin{align}
\hat{p}_{B} &= E[X] \\
&= \frac{\nu}{\beta} \\
\hat{p}_{MAP} &= \frac{\nu-1}{\beta}
\end{align}
$$
ここでガンマ分布$Ga(\nu,1/\beta)$に基づくベイズ推定量を$\hat{p}_{B}$、MAP推定量を$\hat{p}_{MAP}$は上記のように表せることから、事後分布$\displaystyle Ga(\nu+\sum_{i=1}^{n} x_i,1/(\beta+n))$に基づくベイズ推定量$\hat{\lambda}_{B}$、MAP推定量$\hat{\lambda}_{MAP}$は、それぞれ下記のように計算できる。
$$
\large
\begin{align}
\hat{p}_{B} &= E[X] \\
&= \frac{\nu+\sum_{i=1}^{n} x_i}{\beta+n} \\
\hat{p}_{MAP} &= \frac{\nu+\sum_{i=1}^{n} x_i-1}{\beta+n}
\end{align}
$$
上記を元に、いくつかの$\displaystyle Ga(\nu+\sum_{i=1}^{n}x_i,1/(\beta+n))$のパターンに対して、事後分布と$\hat{\lambda}_{B}, \hat{\lambda}_{MAP}$の確認を行う。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
nu, beta = np.array([2., 3., 5., 7., 5., 5.]), np.array([1., 1., 1., 1., 3., 5.])
alpha = 1./beta
x = np.arange(0., 10.1, 0.1)
y = np.zeros([x.shape[0], nu.shape[0]])
for i in range(6):
y[:,i] = stats.gamma.pdf(x, a=nu[i], scale=alpha[i])
plt.subplot(2,3,i+1)
plt.plot(x,y[:,i],color="green")
plt.plot(np.repeat(nu[i]/beta[i],20),np.linspace(0,stats.gamma.pdf(nu[i]/beta[i]-0.01,a=nu[i],scale=alpha[i]),20),"b--", label="lambda_B")
plt.plot(np.repeat((nu[i]-1)/beta[i],20),np.linspace(0,stats.gamma.pdf((nu[i]-1)/beta[i]-0.01,a=nu[i],scale=alpha[i]),20),"r--", label="lambda_MAP")
plt.title("nu+x_1+...+x_n={}, 1/(beta+n)=1/{:.0f}".format(nu[i],beta[i]))
plt.legend(loc=4)
plt.show()・実行結果
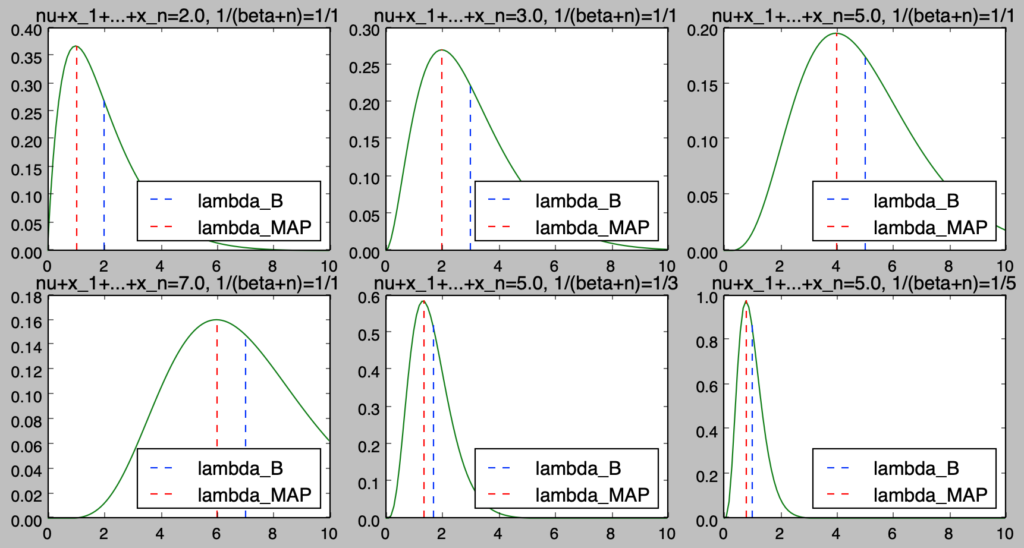

[…] 具体的な計算を下記で取り扱った。https://www.hello-statisticians.com/python/stat_program7.html […]