ブログ

当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.6.2$節「相関係数」の内容を元に$2$変数の相関を確認するにあたって用いられることの多い相関係数に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。

・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

改訂版　日本統計学会公式認定　統計検定２級対応　統計学基礎

2,420円(05/16 23:01時点)

Amazon

相関係数の概要

概要

「$1.6.1$ 散布図と相関」では$2$変数の相関を散布図を元に確認しましたが、散布図のように定性的ではなく定量的に相関を計算するのが当記事で取り扱う相関係数です。相関係数は$2$変数それぞれの分散と共分散を用いて定義する指標ですが、詳しくは以下で取り扱います。

必要な数学

相関係数の式の定義にあたっては$\displaystyle \sum$が用いられるので抑えておくと良いです。

また、相関係数はベクトルの内積を元に表すと理解しやすいので、ベクトルと内積を抑えておくと良いと思います。

相関係数

共分散の定義式

$x_1, \cdots , x_n$と$y_1, \cdots , y_n$の平均$\bar{x}, \bar{y}$と標準偏差$s_x, s_y$をそれぞれ下記のように定義します。
$$
\large
\begin{align}
\bar{x} &= \frac{1}{n} \sum_{i=1}^{n} x_i \\
s_x &= \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (x_i-\bar{x})^2 }
\end{align}
$$

$$
\large
\begin{align}
\bar{y} &= \frac{1}{n} \sum_{i=1}^{n} y_i \\
s_y &= \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i-\bar{y})^2 }
\end{align}
$$

このとき$x, y$の共分散$s_{xy}$は下記のように定義されます。
$$
\large
\begin{align}
s_{xy} = \frac{1}{n} \sum_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y})
\end{align}
$$

共分散の解釈

共分散の解釈にあたっては下記のように$(\bar{x},\bar{y})$に着目して考えると良いです。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(0)

x = stats.uniform.rvs(0., 10., size=100)
y = x + stats.norm.rvs(0, 1, size=100)

mean_x, mean_y = np.mean(x), np.mean(y)

plt.scatter(x,y,color="limegreen")
plt.plot(np.linspace(0., 10., 100), mean_y*np.ones(100), "g--")
plt.plot(mean_x*np.ones(100), np.linspace(np.min(y)-1., np.max(y)+1., 100), "g--")

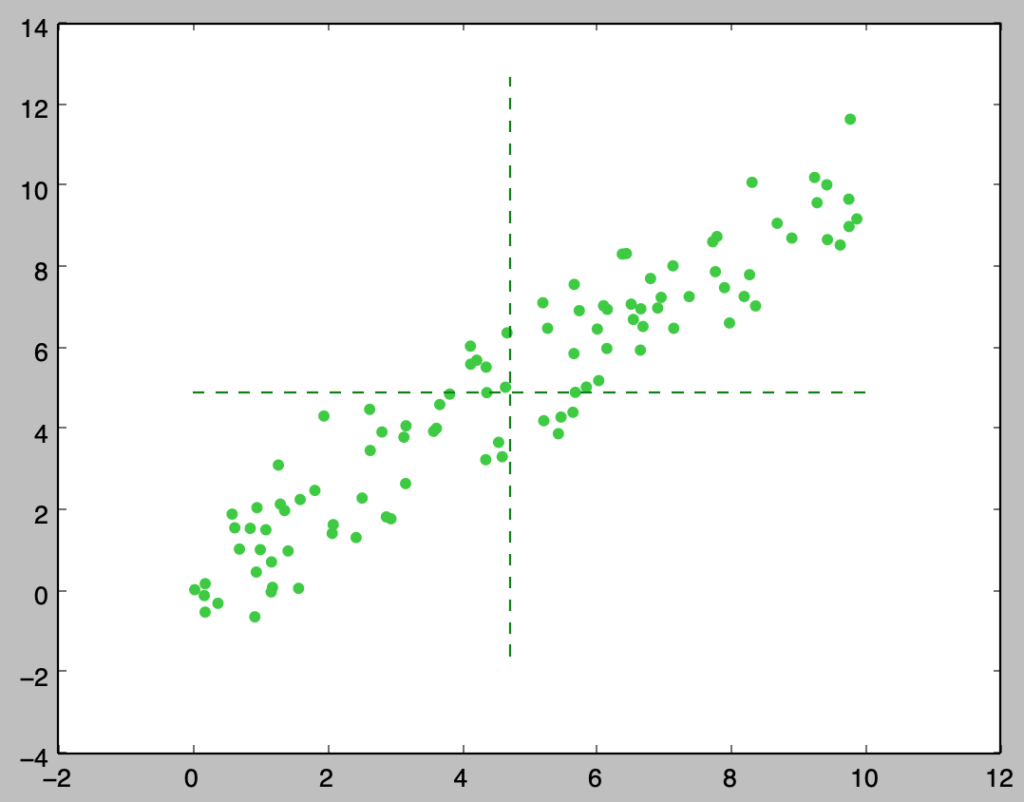
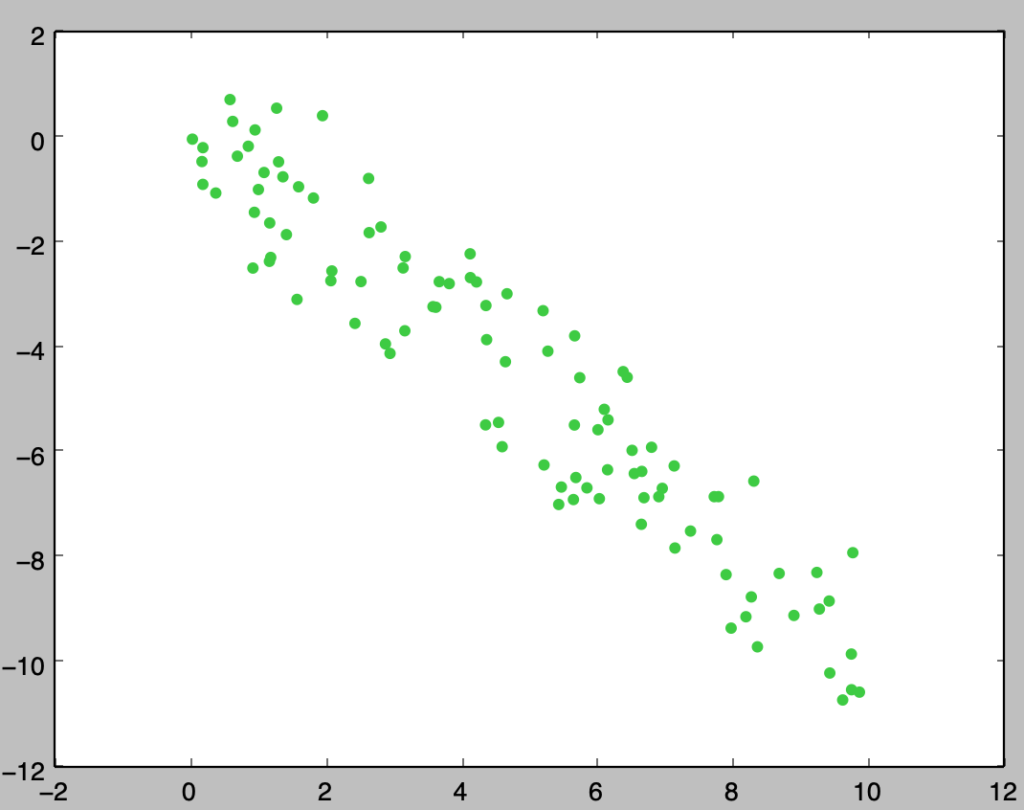
plt.show()

・実行結果

上記は正の相関がある観測値の散布図に直線$x=\bar{x}, y=\bar{y}$を書き入れたものです。上記より、正の相関がある場合は$(\bar{x},\bar{y})$の右上と左下にサンプルが多いことが確認できます。ここで共分散の式における$(x_i-\bar{x})(y_i-\bar{y})$は$(\bar{x},\bar{y})$の右上と左下に$(x_i,y_i)$があれば正、左上と右下に$(x_i,y_i)$があれば負の値を取ります。よって、共分散は$(x_i,y_i)$が$(\bar{x},\bar{y})$を基準にどの位置にあることが多いかを表す指標であると解釈できます。

相関係数の定義

共分散$s_{xy}$は$s_{xy}>0$であれば正の相関、$s_{xy}<0$であれば負の相関を表します。このとき相関の強さを判断するにあたっては、共分散は$x, y$のそれぞれの分散の値が大きくなるにつれて大きくなるのでスケールを調整する必要があります。

スケールの調整にあたって、相関係数$r_{xy}$を下記のように定義します。
$$
\large
\begin{align}
r_{xy} = \frac{s_{xy}}{s_x s_y}
\end{align}
$$

相関係数の解釈

相関係数を用いる際には下記の$3$点に注意すると良いです。

① 相関関係と因果関係は異なるので、因果関係を示す場合はそれぞれの変数の持つ意味を含めて考察する必要がある。
② 因果関係がなくても相関係数が大きい場合があり、このような場合を擬相関(spurious correlation)という。
③ 相関係数は$2$変数が線形式で表せる前提を置いているので非線形の関数で近似できる場合などは散布図などから判断する必要がある。

ベクトルの内積を用いた相関係数の表現

ベクトル$\mathbf{x}-\bar{\mathbf{x}}, \mathbf{y}-\bar{\mathbf{y}}$をそれぞれ下記のように定めます。
$$
\large
\begin{align}
\mathbf{x}-\bar{\mathbf{x}} &= \left( \begin{array}{c} x_1-\bar{x} \\ \vdots \\ x_n-\bar{x} \end{array} \right) \\
\mathbf{y}-\bar{\mathbf{y}} &= \left( \begin{array}{c} y_1-\bar{y} \\ \vdots \\ y_n-\bar{y} \end{array} \right)
\end{align}
$$

このとき相関係数は下記のように表すことができます。
$$
\large
\begin{align}
r_{xy} &= \frac{s_{xy}}{s_x s_y} \\
&= \frac{\displaystyle \sum_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sqrt{\sum_{i=1}^{n} (x_i-\bar{x})^2 \cdot \sum_{i=1}^{n} (y_i-\bar{y})^2}} \\
&= \frac{(\mathbf{x}-\bar{\mathbf{x}}) \cdot (\mathbf{y}-\bar{\mathbf{y}})}{|\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}|}
\end{align}
$$

さらにここで下記が成立します。
$$
\large
\begin{align}
r_{xy} &= \frac{(\mathbf{x}-\bar{\mathbf{x}}) \cdot (\mathbf{y}-\bar{\mathbf{y}})}{|\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}|} \\
(\mathbf{x}-\bar{\mathbf{x}}) \cdot (\mathbf{y}-\bar{\mathbf{y}}) &= |\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}| r_{xy} \\
&= |\mathbf{x}-\bar{\mathbf{x}}||\mathbf{y}-\bar{\mathbf{y}}| \cos{\theta}
\end{align}
$$

上記では内積の定義に基づき$r_{xy}=\cos{\theta}$のように表しましたが、$\theta$はベクトル$\mathbf{x}-\bar{\mathbf{x}}, \mathbf{y}-\bar{\mathbf{y}}$のなす角であると解釈することができます。

当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.6.1$節「散布図」の内容を元に$2$変数の相関を確認するにあたって用いられることの多い散布図に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。

・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

改訂版　日本統計学会公式認定　統計検定２級対応　統計学基礎

2,420円(05/16 23:01時点)

Amazon

散布図と相関の概要

概要

基本的に賃貸マンションの家賃は部屋の大きさが大きくなるにつれて高くなる傾向にあります。このように「家賃」と「部屋の大きさ」のような$2$つの変数の関係を相関(correlation)といいます。

$2$変数の相関は主に「正の相関」、「負の相関」、「無相関」の$3$種類ありますが、「片方が増えればもう片方も増える」場合は「正の相関」、「片方が増えればもう片方は減る」場合は「負の相関」、「$2$変数が連動しない」場合は「無相関」のようにそれぞれ表します。

相関を調べる際には主に「散布図の作成」と「相関係数の計算」の$2$つの手段があり、大概の場合はどちらも用いて相関があるかどうかを調べます。相関係数は「$1.6.2$ 相関係数」で取り扱うので、当記事では「散布図」に関して以下取り扱いました。

必要な数学

当記事では図を元に定性的な確認・考察を行うので、数学知識は基本的には必要ありません。

散布図と相関

散布図と正の相関

正の相関を持つ散布図は下記を実行することで作成できます。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(0)

x = stats.uniform.rvs(0., 10., size=100)
y = x + stats.norm.rvs(0, 1, size=100)

plt.scatter(x,y,color="limegreen")
plt.show()

・実行結果

散布図と負の相関

負の相関を持つ散布図は下記を実行することで作成できます。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(0)

x = stats.uniform.rvs(0., 10., size=100)
y = -x + stats.norm.rvs(0, 1, size=100)

plt.scatter(x,y,color="limegreen")
plt.show()

・実行結果

散布図と無相関

当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.4.3$節「外れ値」の内容を元に例外的な値である観測値の外れ値の概要や簡単な取り扱い方に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。

・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

改訂版　日本統計学会公式認定　統計検定２級対応　統計学基礎

2,420円(05/16 23:01時点)

Amazon

外れ値の概要

概要

実験・調査・観測値の入力などの際のミスや分布のばらつきが大きいときなどに起因して、平均や中央値を基準に極めて大きい観測値や極めて小さい観測値が観測される場合があります。このような値を「外れ値(outlier)」といいます。

入力ミスなどによる「外れ値」は修正が必要である一方で、正しい観測値である場合も母集団の傾向を掴むにあたって除外して考える場合もあります。逆に「異常検知」のように「外れ値」にフォーカスして原因の究明を行うなどもあります。

「外れ値」かどうかを判定するにあたっては「標準化得点」や「箱ひげ図」などを用いることが多いです。当記事では以下、外れ値の判定や取り扱いに関して取りまとめを行いました。

必要な数学

中央値、四分位数などを主に取り扱うので、$2$級範囲では数学知識は特に必要ありません。

外れ値の判定

標準化得点と外れ値

詳しくは「$1.3.2$ 標準化得点」で取り扱いましたが、観測値$x_1, \cdots , x_n$の平均$\bar{x}$、標準偏差$S$を元に標準化得点$z_i$は下記のように定義されます。
$$
\large
\begin{align}
z_i = \frac{x_i-\bar{x}}{S}
\end{align}
$$

また、標準化得点$z_i$を元に偏差値は下記のように定義されます。
$$
\large
\begin{align}
10 z_i + 50
\end{align}
$$

$z_i=1, 2$はそれぞれ偏差値$60$と$70$に対応するので、$|z_i| \geq 2$などを基準に外れ値を定めることができます。$x_i$が正規分布に基づいて得られるとき、$z_i>1$の確率は約$15.87$％、$z_i>2$の確率は約$2.28$％、$z_i>3$の確率は約$0.13$％がそれぞれ対応します。

異常検知の際などは$z_i>3$が用いられることが多いようなので、$1,000$回に$1$回起こるような事象は外れ値であると解釈することもできます。このように外れ値の判定基準は問題によりけりですが、標準化得点を用いることで外れ値の判定が行えるということは抑えておくと良いと思います。

箱ひげ図と外れ値

下記を実行することで「$1.4.2$ 箱ひげ図」で作成した図と同様な図を作成することができます。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(0)

x1 = stats.norm.rvs(loc=0,scale=1,size=100)
x2 = stats.norm.rvs(loc=0,scale=1.5,size=100)
x3 = stats.norm.rvs(loc=1,scale=1,size=100)

plt.boxplot([x1, x2, x3])
plt.show()

・実行結果

上記では外れ値は+で表されるので、一番右の箱ひげ図で外れ値が図示されることが確認できます。一方で、ここで生成を行なった観測値は正規分布に基づいて生成を行なった乱数であるので、それほど極端な外れ値は観測できないことも合わせて抑えておくと良いです。

当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.4.2$節「箱ひげ図」の内容を元に$5$数要約の可視化にあたって用いられる箱ひげ図の概要や描き方に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。

・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

改訂版　日本統計学会公式認定　統計検定２級対応　統計学基礎

2,420円(05/16 23:01時点)

Amazon

箱ひげ図の概要

概要

$5$数要約を用いることで四分位範囲や中央値を元に観測値を把握することができますが、単に計算結果だけではなく図を用いて可視化を行うことでより直感的な把握が可能になります。$5$数要約の可視化にあたってよく用いられるのが箱ひげ図(box whisker plot)です。

箱ひげ図は上図のような図であり、第$1$四分位数と第$3$四分位数を元に箱を作成し、中央値を箱の中に書き入れます。ひげの描き方はいくつかあるので詳しくは次節や「$1.4.3.$ 外れ値」などで確認します。

必要な数学

中央値、四分位数を主に取り扱うので、$2$級範囲では数学知識は特に必要ありません。

箱ひげ図

箱ひげ図の解釈

上図のような箱ひげ図の解釈にあたっては、箱によって第$1$四分位数$Q1$と第$3$四分位数$Q2$が表され、箱の中に中央値が記入されることをまず抑えると良いです。ひげの描き方は最大値・最小値を元に作成する場合と、四分位範囲$IQR$を元に作成する場合などがあります。上図では「$1.4.3.$ 外れ値」の内容も考慮し、$Q3 + 1.5 IQR$と$Q1 – 1.5 IQR$を元にひげを作成しました。+のマーカーは例外のような観測値であると解釈しておけば良いです。

Pythonを用いた箱ひげ図の作成

下記を実行することでPythonで箱ひげ図を作成することができます。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(0)

x1 = stats.norm.rvs(loc=0,scale=1,size=100)
x2 = stats.norm.rvs(loc=0,scale=1.5,size=100)
x3 = stats.norm.rvs(loc=1,scale=1,size=100)

plt.boxplot([x1, x2, x3])
plt.show()

・実行結果

上記はx1が$\mathcal{N}(0,1^2)$に基づくサンプル、x2が$\mathcal{N}(0,1.5^2)$に基づくサンプル、x3が$\mathcal{N}(1,1^2)$に基づくサンプルにそれぞれ対応しますが、概ね妥当な結果が得られたことが確認できると思います。

当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.4.1$節「$5$数要約」の内容を元に最小値・第$1$四分位数・中央値・第$3$四分位数・最大値を用いた観測値の要約に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。

・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

改訂版　日本統計学会公式認定　統計検定２級対応　統計学基礎

2,420円(05/16 23:01時点)

Amazon

5数要約の概要

概要

得られた観測値を数字で要約するにあたっては、中央値や四分位数のように大まかにパターンがあるので、表の形式で数字をまとめて取り扱うと作成や解釈がしやすいです。

当記事では最小値・第$1$四分位数・中央値・第$3$四分位数・最大値を元に構成される要約の$5$数要約(five-number summary)について以下具体的な例を元に詳しく確認します。変数の分類で取り扱った例を同じく取り扱うので合わせて確認しておくと良いです。

必要な数学

中央値、四分位数を主に取り扱うので、$2$級範囲では数学知識は特に必要ありません。

5数要約

上記の詳細は下記より入手することができます。
http://www.tokyo-tosho.co.jp/books/978-4-489-02227-2/

家賃、大きさ、築年数の$5$数要約は下記のように作成できます。

当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.3.5$節「範囲・四分位範囲」の内容を元に、左右対称でない分布の散らばり度合いを表す指標に用いられる四分位範囲に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。

・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic

改訂版　日本統計学会公式認定　統計検定２級対応　統計学基礎

2,420円(05/16 23:01時点)

Amazon

「範囲・四分位範囲」の概要

概要

観測値の散らばりを表すにあたっては分散に基づく標準偏差が用いられることが多い一方で、標準偏差は平均を用いて計算することから左右対称でない分布に対しては適切ではない場合が多いです。

このような場合に中心を表す指標である中央値・最頻値と同時に用いられることが多いのが「範囲・四分位範囲」です。範囲は最大値・最小値が外れ値である場合も多いので、実用的には四分位範囲が用いられることが多いです。以下、範囲・四分位範囲に関して詳しく確認を行います。

必要な数学

四分位範囲は基本的に中央値と同様に考えるので、定義さえ理解できれば数学的な表現はそれほど重要ではありません。

範囲・四分位範囲

範囲

範囲$R$は「最大値$-$最小値」で定義されます。範囲を考えることで値がどのくらい散らばっているかを判断することができます。たとえば試験の最高点と最低点を元に範囲を計算することで、試験の各問題の難易度の評価などを行うことが可能です。

範囲は左右対称でない分布に関しても計算することができますが、外れ値が存在する場合に範囲が大きくなるなど、全体の傾向を見るには適さない場合があります。よって、一般に散らばり度合いを確認する際は次項で確認する四分位範囲を用いることが多いです。

四分位範囲

四分位範囲は、中央値と同じ要領で考えると理解しやすいです。観測値を小さい順に並べた際に、全体の$25$％、$50$％、$75$％にある値をそれぞれ$Q1, Q2, Q3$とおきます。このとき$Q1, Q2, Q3$をそれぞれ第$1$四分位数、第$2$四分位数、第$3$四分位数といいます。

ここで第$2$四分位数の$Q2$が中央値に一致することも合わせて抑えておくと良いです。また四分位範囲(interquartile range)を$IQR$とおくと、$IQR$は下記のように定義されます。
$$
\large
\begin{align}
IQR = Q3 – Q1
\end{align}
$$

上記の$1/2$の$IQR/2$を四分位偏差(quartile deviation)といい、分布が左右対称でない場合に標準偏差の代わりに用いられることが多いです。