当まとめでは統計検定$2$級の公式テキストの副教材に用いることができるように、統計学入門に関して取り扱います。当記事では「統計検定$2$級対応 統計学基礎」の$1.4.3$節「外れ値」の内容を元に例外的な値である観測値の外れ値の概要や簡単な取り扱い方に関して取り扱いました。
統計検定$2$級のテキストとの対応がわかりやすいように、目次を「統計検定$2$級対応 統計学基礎」と対応させました。学びやすさの観点からあえて目次を対応させましたが、当まとめは「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
・統計検定$2$級対応・統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
外れ値の概要
概要
実験・調査・観測値の入力などの際のミスや分布のばらつきが大きいときなどに起因して、平均や中央値を基準に極めて大きい観測値や極めて小さい観測値が観測される場合があります。このような値を「外れ値(outlier)」といいます。
入力ミスなどによる「外れ値」は修正が必要である一方で、正しい観測値である場合も母集団の傾向を掴むにあたって除外して考える場合もあります。逆に「異常検知」のように「外れ値」にフォーカスして原因の究明を行うなどもあります。
「外れ値」かどうかを判定するにあたっては「標準化得点」や「箱ひげ図」などを用いることが多いです。当記事では以下、外れ値の判定や取り扱いに関して取りまとめを行いました。
必要な数学
中央値、四分位数などを主に取り扱うので、$2$級範囲では数学知識は特に必要ありません。
外れ値の判定
標準化得点と外れ値
詳しくは「$1.3.2$ 標準化得点」で取り扱いましたが、観測値$x_1, \cdots , x_n$の平均$\bar{x}$、標準偏差$S$を元に標準化得点$z_i$は下記のように定義されます。
$$
\large
\begin{align}
z_i = \frac{x_i-\bar{x}}{S}
\end{align}
$$
また、標準化得点$z_i$を元に偏差値は下記のように定義されます。
$$
\large
\begin{align}
10 z_i + 50
\end{align}
$$
$z_i=1, 2$はそれぞれ偏差値$60$と$70$に対応するので、$|z_i| \geq 2$などを基準に外れ値を定めることができます。$x_i$が正規分布に基づいて得られるとき、$z_i>1$の確率は約$15.87$%、$z_i>2$の確率は約$2.28$%、$z_i>3$の確率は約$0.13$%がそれぞれ対応します。
異常検知の際などは$z_i>3$が用いられることが多いようなので、$1,000$回に$1$回起こるような事象は外れ値であると解釈することもできます。このように外れ値の判定基準は問題によりけりですが、標準化得点を用いることで外れ値の判定が行えるということは抑えておくと良いと思います。
箱ひげ図と外れ値
下記を実行することで「$1.4.2$ 箱ひげ図」で作成した図と同様な図を作成することができます。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(0)
x1 = stats.norm.rvs(loc=0,scale=1,size=100)
x2 = stats.norm.rvs(loc=0,scale=1.5,size=100)
x3 = stats.norm.rvs(loc=1,scale=1,size=100)
plt.boxplot([x1, x2, x3])
plt.show()・実行結果
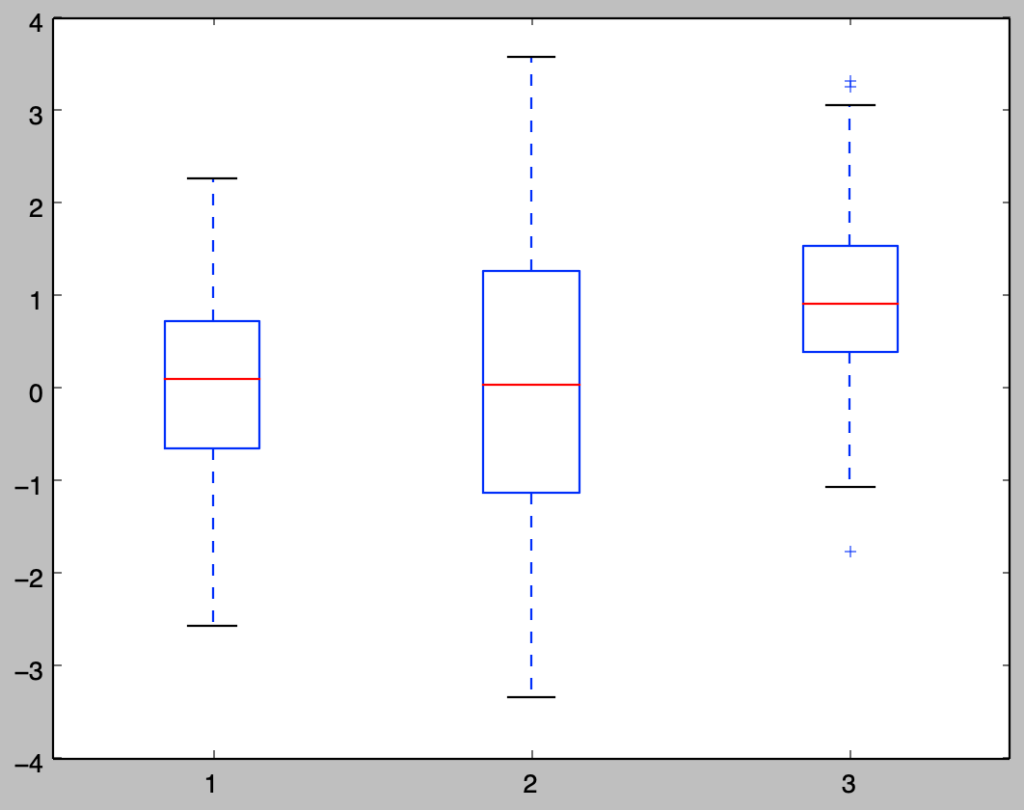
上記では外れ値は+で表されるので、一番右の箱ひげ図で外れ値が図示されることが確認できます。一方で、ここで生成を行なった観測値は正規分布に基づいて生成を行なった乱数であるので、それほど極端な外れ値は観測できないことも合わせて抑えておくと良いです。

[…] 箱ひげ図は上図のような図であり、第$1$四分位数と第$3$四分位数を元に箱を作成し、中央値を箱の中に書き入れます。ひげの描き方はいくつかあるので詳しくは次節や「$1.4.3.$ 外れ値」などで確認します。 […]